12 Билет Задача 1

Имеем данные по двум предприятиям, которые изготовляют одинаковую продукцию.

Проанализировать изменение средних затрат времени на производство единицы продукции по двум предприятиям за 2006 и 2007 года. Объяснить выбор средней величины и полученные результаты расчетов.

Номер предприятия	2006 г.		2007 г.
	затр времени на 1 прод, час.	Изг прод, шт.	затр времени на 1 прод, час.	Затр врем на всю прод, час.
1	2	150	1,9	380
2	3	250	3	840

Решение

Рассчитаем средние по 2006г. и 2007г., а потом их сравним. 1.2006г.: Так как условие задачи представлено в виде вариант (затраты времени на единицу продукции) и частот (изготовлено продукции) то применим среднюю арифметическую и так как варианты имеют различный вес то взвешенную.

час.

2.2007г.: Так как условие представлено в виде вариант (затраты времени на единицу продукции) и произведения вариант на частоты (Затраты времени на всю продукцию = затраты времени на единицу продукции * изготовлено продукции) то применим среднюю гармоническую.

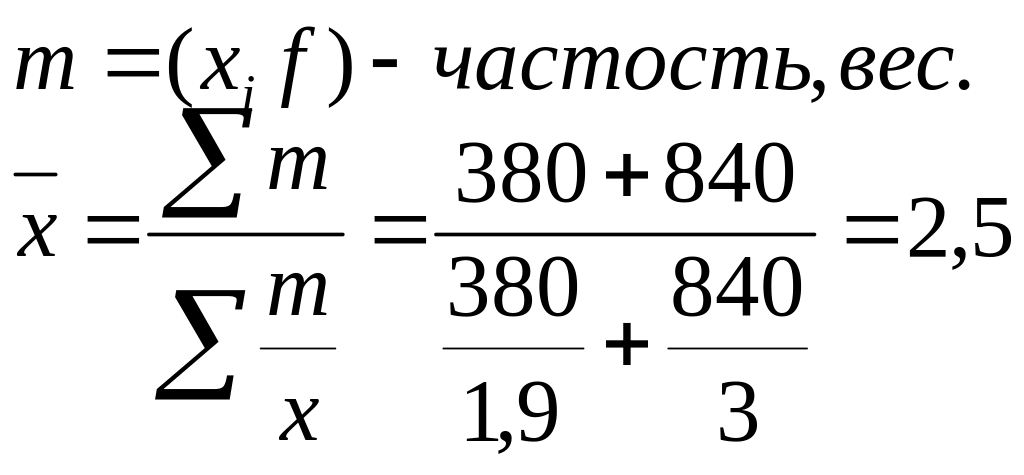час. По полученным данным мы видим, что средние затраты времени на единицу продукции в 2007 году по сравнению с 2006 снизились на 0,1 часа или в 0,96 раз.

Задача 2

Имеем данные по предприятиям города. С помощью индексов средних величин проанализировать динамику продуктивности труда вместе по двум предприятиям. С помощью индивидуальных индексов, показать, как изменилась продуктивность труда на каждом предприятии отдельно. Дать экономическую интерпретацию полученным показателям.

Решение

Динамику средних уровней характеризует индекс переменного состава, т.е. он характеризует изменение индивидуального значения индексируемой величины, так и в результате изменения структуры совокупности.

Или 101,5%, т.е. производительность труда под влиянием всех факторов по двум предприятиям увеличилась на 1,5%. Для анализа влияния только индексируемой величины на изменение средней рассчитывают индекс постоянного состава. Обычно это агрегатные индексы.

Номер предприятия	Базовый период		Отчетный период
	Вал прод в сравн-х ценах, тыс. грн.	Пром-произв персонал, чел.	Вал прод в сравн-х ценах, тыс. грн.	Пром-произвй персонал, чел.	Индекс произв труда по пр, %
1	40200	6700	42000	7000	100
2	28000	7000	29500	7100	103,9

Или 102%, т.е. производительность труда по двум предприятиям под влиянием увеличения валовой продукции увеличилась на 2%.

Индекс постоянного состава или индекс структурных сдвигов.

Или производительность труда по двум предприятиям уменьшилась на 0,5% за счет структурных изменений промышленно-производственного персонала.

Индивидуальные индексы показывают, что на первом предприятии производительность труда не изменилась, а на втором увеличилась на 3,9% в отчетном периоде по сравнению с базисным.