Теорема. Всякая частично рекурсивная функция f является вычислимой функцией.

Тезис ЧЕРЧА: Числовая функция тогда и только тогда алгоритмически вычислима, когда она частично рекурсивна.

44. Определение алфавита, слова в теории нормальных алгоритмов Маркова. Понятия пустого слова и подслова. Определение марковской подстановки. Результат марковской подстановки. Соединение слов. Понятие расширения алфавита.

Алфавитом (как и прежде) называется любое непустое множество. Его элементы называются буквами, а любые последовательности букв — словами в данном алфавите. Для удобства рассуждений допускаются пустые слова (они не имеют в своем составе ни одной буквы). Если A и B — два алфавита, причем AєB, то алфавит B называется расширением алфавита A.

Слова будем обозначать латинскими буквами: P,Q,R (или этими же буквами с индексами). Одно слово может быть составной частью другого слова. Тогда первое называется подсловом второго или вхождением во второе.

Марковской подстановкой называется операция над словами, задаваемая с помощью упорядоченной пары слов (P,Q), состоящая в следующем. В заданном слове R находят первое вхождение слова P (если таковое имеется) и, не изменяя остальных частей слова R, заменяют в нем это вхождение словом Q. Полученное слово называется результатом применения марковской подстановки (P,Q) к слову R. Если же первого вхождения P в слово R нет (и, следовательно, вообще нет ни одного вхождения P в R), то считается, что марковская подстановка (P,Q) неприменима к слову R.

45. Определение алгоритма применимого к слову. Определение алгоритма над алфавитом. Простая и заключительная подстановки в теории нормальных алгоритмов Маркова. Схема алгоритма.

Пусть Р есть слово в алфавите А; говорят, что алгоритм α применим к слову Р, если Р содержится в области определения α.

Если алфавит В является расширением алфавита А, то всякий алгоритм в алфавите В называется алгоритмом над алфавитом А.

Для обозначения марковской подстановки (Р, Q) используется запись Р —> Q. Она называется формулой подстановки (Р, Q). Некоторые подстановки (Р, Q) будем называть заключительными. Для обозначения таких подстановок будем использовать запись Р —>. Q, называя ее формулой заключительной подстановки.

Слово Р называется левой частью, a Q — правой частью в формуле подстановки.

Конечный список формул подстановки в алфавите А, называется схемой алгоритма и порождает следующий алгоритм в алфавите А.

46. Определение нормального алгоритма Маркова в алфавите А.

Упорядоченный конечный список формул подстановок в алфавите называется схемой (или записью) нормального алгоритма в .

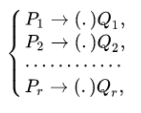
Данная схема определяет (детерминирует) алгоритм преобразования слов, называемый нормальным алгоритмом Маркова. Дадим его точное определение.

47. Описание работы нормального алгоритма Маркова со словами. Определение нормально вычислимой функции, заданной на некотором множестве слов некоторого алфавита. Примеры нормально вычислимых функций.

Пример МТ: вычисляющей функцию x+1;

48. Пример построения нормального алгоритма для функции.

49. Теорема о частичной вычислимости по Маркову всякой частично рекурсивная функции и следствие к ней. Принцип нормализации. Совпадение класса всех нормально вычислимых функций с классом всех функций, вычислимых по Тьюрингу. Эквивалентность различных теорий алгоритмов.

Теорема 1: Всякая частично рекурсивная функция (общерекурсивная) является частично вычислимой (вычислимой) по Маркову функцией.

Теорема 2: Всякая частичная функция, частично вычислимая (вычислимая) по Маркову, является частично рекурсивной (общерекурсивной) функцией.

"Принцип нормализации Маркова": Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально вычислима.

Следующие классы функций {заданных на натуральных числах и принимающих натуральные значения) совпадают:

а) класс всех функций, вычислимых по Тьюрингу;

б) класс всех частично рекурсивных функций;

в) класс всех нормально вычислимых функций.

Алгоритмы H1 и H2 эквивалентны относительно алфавита A, если области применимости H1 и H2 относительно алфавита A совпадают и для любого слова P из этой области выполняется равенство H1(P) = H2(P).

50. Машина Тьюринга (МТ). Основные узлы, функционирование. Разновидности МТ. Данные МТ. Элементарные шаги МТ. Применение МТ к словам. Определение заключительного слова по заданному начальному слову и системе команд. Конструирование МТ: задание внешнего алфавита, множества состояний и системы команд. Композиция МТ.

Машина Тьюринга (МТ) состоит из двух частей – ленты и автомата.

Лента используется для хранения информации. Она бесконечна в обе стороны и разбита на клетки. В каждой клетке может быть записан один символ или ничего не записано. Автомат – это активная часть МТ. В каждый момент он размещается под одной из клеток ленты и видит её содержимое. Кроме того, в каждый момент автомат находится в одном из состояний. Находясь в некотором состоянии, автомат выполняет какую-то определённую операцию

МТ работает тактами (по шагам), которые выполняются один за другим. На каждом такте автомат МТ выполняет три следующих действия, причем обязательно в указанном порядке:

1) записывает некоторый символ S в видимую клетку (в частности, может быть записан тот же символ, что и был в ней, тогда содержимое этой клетки не меняется);

2) сдвигается на одну клетку влево (L), либо на одну клетку вправо (R), либо остается неподвижным ( ).

3) переходит в некоторое состояние q (в частности, может остаться в прежнем состоянии).

Чтобы задать конкретную машину Тьюринга, требуется описать для нее следующие составляющие:

● Внешний алфавит. Конечное множество (например, А), элементы которого называются буквами (символами). Одна из букв этого алфавита (например, а0) должна представлять собой пустой символ.

● Внутренний алфавит. Конечное множество состояний головки (автомата). Одно из состояний (например, q1) должно быть начальным (запускающим программу). Еще одно из состояний (q0) должно быть конечным (завершающим программу) – состояние останова.

● Таблица переходов. Описание поведения автомата (головки) в зависимости от состояния и считанного символа.

Виды МТ:

• Многодорожечная машина Тьюринга

• Машина Тьюринга с полубесконечной лентой

• Многоленточная машина Тьюринга

Автомат машины Тьюринга в процессе своей работы может выполнять следующие действия:

● Записывать символ внешнего алфавита в ячейку (в том числе и пустой), заменяя находившийся в ней (в том числе и пустой).

● Передвигаться на одну ячейку влево или вправо.

● Менять свое внутреннее состояние.

Если требуется написать достаточно сложную программу, для упрощения процесса программирования применяют операции композиции машин Тьюринга, т.е. построение сложной машины из более простых, при этом используют две операции: умножение машин Тьюринга и итерация машин Тьюринга.

51. Функция, вычислимая по Тьюрингу. Функция правильно вычислимая по Тьюрингу. Запись на ленте МТ значений аргументов функций. Запись результата вычислений на ленте. Зацикливание машины. Эквивалентность и суперпозиция машин Тьюринга. Тезис Тьюринга.

Ф-я наз-ся вычислимой по Тьюрингу, если существует машина Тью­ринга, вычисляющая ее, т.е. такая машина Тьюринга, которая вычисляет ее значения для тех наборов значений аргументов, для которых функция определена, и работающая вечно, если функ­ция для данного набора значений аргументов не определена.

Функция f называется правильно вычислимой по Тьюрингу, если существует машина Тьюринга Т, которая ее правильно вычисляет.

Теорема о зацикливании : Проблема зацикливания машины Тьюринга не является частично разрешимой.

МТ зацикливается, никогда не попадая на такт останова (например, автомат на каждом шаге сдвигается вправо и потому не может остановиться, т.к. лента бесконечна). В этом случае говорят, что МТ неприменима к заданному входному слову. Ни о каком результате при таком исходе не может идти и речи.

Лента, на которой записывается результат вычислений, движется со скоростью программной ленты и поэтому запись результата не вызывает замедления работы машины. Результат, записанный на ленту в двоичной системе, переводится в десятичную и отпечатывается на бумаге.

Эквивалентность МТ и частично-рекурсивных функций означает, что всякая частично-рекурсивная функция оказывается вычислимой по Тьюрингу и наоборот.

Если функции f(x₁,x₂,…,x_n), g₁ (x₁,x₂,…,x_m), …, g_n (x₁,x₂,…,x_m) правильно вычислимы по Тьюрингу, то правильно вычислима и сложная функция (суперпозиция функций):

φ(x₁,x₂,…,x_n)=f( g₁ (x₁,x₂,…,x_m),…, g_n (x₁,x₂,…,x_m)).

Тезис: любая функция, которая может быть вычислена физическим устройством, может быть вычислена машиной Тьюринга.