Правила вывода
1.
Правило подстановки.
Если
выводимая формула, то
также выводимая формула, каковы бы ни
были переменное высказывание А и формула
:
.
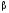2.
Правило
заключения.
Если
и
выводимые формулы исчисления высказываний,
то
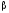
также выводимая формула:
.
-
Некоторые составные правила ИВ (правила силлогизма, перестановки посылок, соединения посылок, разъединения посылок и т.д).
-
Понятие выводимости формулы из набора формул ИВ. Теорема дедукции.
Определение
выводимости
формулы
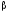из формул
,
называемых исходными:
-
каждая формула
выводима из формул; -
каждая выводимая в исчислении высказываний формула выводима из
; -
если формулы
и
выводимы из
,
то формула
также выводима из
.
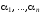Утверждение,
что формула
выводима из
,
мы будем обозначать так:
. (1)
Если
n=0,
т.е. когда формул
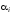вовсе нет, мы будем считать, что
является просто выводимой формулой
исчисления высказываний. Выражение (1)
в этом случае, естественно, превращается
в
.
Теорема
дедукции.
Если
формула
,
то
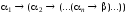
выводимая формула.
-
Эквивалентные формулы в ИВ. Теорема эквивалентности.
Для
сокращения записи, формулу, имеющую вид
,
мы будем сокращенно записывать в виде
~
и называть эквивалентностью.
Будем говорить, что формулы a и b эквивалентны, если имеет место
~b.
Основные свойства соотношения эквивалентности:
-
Если эквивалентно , то и эквивалентно (симметричность).
-
Если эквивалентно и эквивалентно , то эквивалентно .
Теореме
эквивалентности.
Если
в формуле
заменить какую-нибудь ее часть
эквивалентной формулой
,
то вновь полученная формула
будет эквивалентна прежней, именно:
.
-
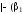
Проблемы аксиом ИВ (разрешимость, непротиворечивость, полнота, независимость).
-
РАЗРЕШИМОСТЬ - заключается в том, что должен существовать алгоритм, позволяющий для любой заданной формулы ИВ определять, яв-ся она выводимой или нет. Для проверки разрешимости достаточно рассмотреть формулу ИВ как АВ и проверить, будет ли она тождественно истинной. Если в АВ она тождественно истинна, то она выводима в ИВ.
-
НЕПРОТИВОРЕЧИВОСТЬ - какова бы ни была формула а(альфа), никогда а и (not a) не могут быть одновременно из аксиом этого исчисления с помощью указанных в нем правил ИВ непротиворечиво.
-
ПОЛНОТА - I. аксиоматич. исчисл. наз-ся полным в УЗКОМ смысле, если добавление к списку его аксиом любой невыводимой исчисл. форм. в кач-ве новой аксиомы приводит к противоречивому исчислению. ТЕОРЕМА: ИВ полное в узком смысле. II. аксиоматич. исчисление называется полным в ШИРОКОМ смысле, если любая тождественно истинная формула в нем доказуема (выводима).
-
НЕЗАВИСИМОСТЬ аксиом - заключается в невыводимости аксиомы из ост. аксиом по правилам вывода в данной системе. ТЕОРЕМА: Система аксиом ИВ независима.
-
Проверки выводимости формул ИВ методом резолюций.
D1=D1'vA;
D2=D2'v(not A).
D1'vD2' - РЕЗОЛЬВЕНТА дизъюнктов D1 и D2 по переменной A и обозначается resA(D1, D2) = D1'vD2'
Пример: res(A,(notA))=0 т.к. A&(notA)=0.
Если дизъюнкты D1 и D2 не содержат контарных переменных, то дизъюнктов в них не существует.
Пример:
D1=(notA)vBvC;
D2=Av(not B)vС.
resA (D1,D2)=BvCv(not B)vD;
resB (D1,D2)= (notA)vCvAvD.
ТЕОРЕМА:
1) если res(D1,D2) существует и не равен 0, то D1,D2 |- res(D1,D2).
2) если res(D1,D2)=0, то множество дизъюнктов D1,D2 противоречивы.
ТЕОРЕМА о полноте метода резолюции: мн-во дизъюнктов S противоречиво тогда и только тогда, когда существует резольвента вывод. из S, заканчивающийся нулем.
Где S={D1,D2,...Dn} - множество дизъюнктов.
-
Описание логики предикатов (ЛП). Символы ЛП. Логические функции. Предикаты. Предметные области и предметы. Переменные высказывания и предикаты. Элементарные высказывания и элементарные формулы.
Логика предикатов представляет собой развитие алгебры высказываний. Она содержит в себе всю алгебру высказываний. Но, помимо этого, логика предикатов вводит в рассмотрение высказывания, отнесенные к предметам. В ней уже имеется расчленение высказываний на субъект и предикат.
Предикат – это высказывание, в которое можно подставлять аргументы. Если аргумент один – то предикат выражает свойство аргумента, если больше – то отношение между аргументами.