
- •Алгоритм приведения к сднф:
- •Правила вывода
- •Символы логики предикатов
- •Кванторы всеобщности и существования. Свободные и связные переменные лп.
- •Равносильные и приведенные формулы лп. Теорема о существовании приведенной формулы.
- •Выводимость в ип:
- •Логические основы эвм. Простейшие преобразователи информации. Структурная формула. Функциональная схема.
- •Свойства нечетких множеств
- •Алгоритм — это упорядоченный набор однозначных выполнимых шагов.
- •Свойства:
- •Теорема. Всякая частично рекурсивная функция f является вычислимой функцией.
- •Определение алгоритма применимого к слову. Определение алгоритма над алфавитом. Простая и заключительная подстановки в теории нормальных алгоритмов Маркова. Схема алгоритма.
- •Нумерация алгоритмов. Нумерация машин Тьюринга. Существование невычислимых по Тьюрингу функций.
- •Примеры алгоритмически неразрешимых проблем.
Математическая логика ^ ^
1
-
Природа математической логики. Формальная логика. Основные формы мышления (понятие, высказывание, умозаключение). Простые и сложные высказывания. Основные законы формальной логики.
Мат. логика - это наука о средствах и методах мат. доказательств. Мат.логика изучает принципы построения мат. теорий. Предметом мат.логики яв-ся рассуждение.
Формальная логика — наука, изучающая формы мысли — понятия, суждения, умозаключения, доказательства — со стороны их логической структуры.
Алфавит форм. логики состоит из заглавных латинских букв (A,B,C,...) и связок (операторов).
Основные формы мышления:
-
ПОНЯТИЕ - слова и словосочетания, которые описывают существ. признаки предмета.
-
ВЫСКАЗЫВАНИЕ - повествовательное предложение, относительно которого можно сказать, истинно оно или ложно.
-
УМОЗАКЛЮЧЕНИЕ - процесс получения или обоснования новых утверждений из исходных. Исходные утверждения наз-ся ПОСЫЛКАМИ (нач. данными или исходными условиями), а заключит. утверждение - ВЫВОДОМ или заключением.
Простые высказывания не содержат в своем составе других высказываний, а сложные – состоят из нескольких простых высказываний.
3 основных ЗАКОНА форм. логики:
-
ТОЖДЕСТВА - в процессе опред. рассуждения всякое понятие и высказывание должны быть тождественны самим себе. А=А
-
НЕПРОТИВОРЕЧИЯ - невозможно, чтобы одно и то же в одно и то же время было и не было присуще одному и тому же в одном и том же отношении. A ⋀ ¬A=0
-
ИСКЛЮЧЕННОГО ЛИШНЕГО - из 2х противоречивых высказываний одно истинно, другое - ложно, а третьего не дано. A ⋁ ¬A=1
-
Понятие и структура аксиоматических систем.
Аксиоматическая система — любой набор аксиом, из которого некоторые или все аксиомы могут быть в совокупности использованы для логического вывода теорем данной теории.
В них, в явном, не явном или, даже, скрытом виде всегда содержатся три компонента: аксиомы (постулаты) - утверждения, которые предлагается принять без доказательств; теоремы - строгие определения объектов исключительно для целей этой теории (рассуждения, высказывания); правила вывода формул (теорем) - обычно - это всем привычные, часто бессознательно употребляемые логические конструкции.
Это должен быть набор аксиом (постулатов), принимаемых нами без доказательств, удовлетворяющих следующим трем условиям:
1. Независимость (любую из принятых аксиом нельзя вывести из остальных, так, что выведенная из других аксиома является не аксиомой, а теоремой)
2. Непротиворечивость (система аксиом не порождает противоречащих друг другу утверждений, то есть, ни из какой аксиомы не следует утверждение и его отрицание)
3. Полнота (систему нельзя дополнить независимым от уже принятых аксиом утверждением, то есть никакая дополнительная аксиома не может быть выведена из уже имеющихся).
-
Понятие и структура формальных систем.

ТЕОРЕМА ФС:
-
аксиома ФС - теорема ФС.
-
если все посылки некоторого правила ФС яв-ся теоремами ФС, то заключение этого правила яв-ся теорема системы.
-
Основные логические операции алгебры высказываний (АВ). Пропозиционная переменная. Постоянные и переменные высказывания АВ.
Для обозначения простых высказываний используют большие латинские буквы A, B, …, а для их значений – 1 (истина) и 0 (ложь). Переменные A, B,… называют ПОПОЗИЦИОННЫМИ ПЕРЕМЕННЫМИ (propositio – предложение-высказывание).
Символы 0 и 1 - логические константы (ПОСТОЯННЫЕ ВЫСКАЗЫВАНИЯ АВ), латинские буквы A, B, C, … – логические переменные (ПЕРЕМЕННЫЕ ВЫСКАЗЫВАНИЯ АВ).
ЛОГИЧЕСКОЙ ОПЕРАЦИЕЙ называется способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Основные логические операции:
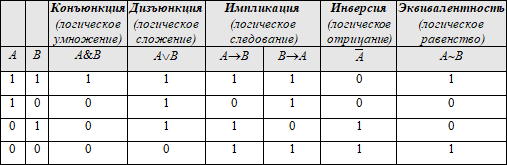
Порядок приоритетности логических операций: 1) инверсия, 2) конъюнкция; 3) дизъюнкция; 4) импликация и эквивалентность. Для изменения порядка действий, используются скобки.
-
Определение формулы АВ. Равносильность формул. Важнейшие примеры равносильных формул.
ФОРМУЛОЙ АВ называется выражение, составленное по определенным правилам из пропозиционных переменных, логических связок и скобок.
-
Пропозициональная переменная является формулой.
-
Если А формула, то
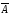 тоже формула.
тоже формула. -
Если A и B формулы, то (AB), (AB), (AB) тоже формулы.
-
Никаких других формул нет.
Две
формулы и
называются равносильными
(=),
если при любых значениях
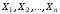 ,
где
,
где
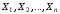 – совокупность всех переменных, входящих
в и ,
эти формулы принимают одинаковые
значения.
– совокупность всех переменных, входящих
в и ,
эти формулы принимают одинаковые
значения.

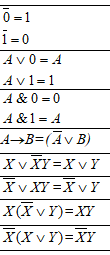
-
Двойственные операции и двойственные формулы АВ. Закон двойственности.
Будем говорить, что операция & двойственная операции и наоборот.
Формулы
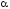 и
и
![]() называются двойственными,
если одна получается из другой заменой
каждой операции на двойственную.
называются двойственными,
если одна получается из другой заменой
каждой операции на двойственную.
Закон
двойственности.
Если
формулы
и
равносильны, то двойственные им формулы
 и
и
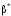 также равносильны.
также равносильны.
Пример.
Найти
формулу двойственную формуле
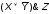 .
.
Решение.
Для этого по определению следует заменить
операции на двойственные. Тогда получим,
что двойственной будет формула
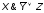
-
Тождественно истинные, выполнимые и невыполнимые формулы АВ.
ТОЖДЕСТВЕННО ИСТИННАЯ формула - если она при всех значениях входимых в нее переменных высказываний принимает значение 1. пример: X\/(¬X).
ВЫПОЛНИМАЯ формула - если она принимает значение 1 при некоторых значениях входящих в нее переменных высказываний. пример: X.
НЕВЫПОЛНИМАЯ формула (тождественно ложная) - если она при всех значениях входящих в нее переменных высказываний принимает значение 0. пример: X\/(¬X).
-
Проблема разрешения в алгебре высказываний. Элементарные произведения и суммы. Теорема о тождественной истинности элементарной суммы. Теорема о тождественной ложности элементарного произведения.
Проблемой разрешения для алгебры высказываний называют следующую проблему: существует ли алгоритм, позволяющий для произвольной логической формулы в конечное число шагов выяснить, является ли она тождественно истинной (или тождественно ложной)?
Элементарной
дизъюнкцией (суммой)
называется дизъюнкция (сумма) логических
переменных и их отрицаний. Например,
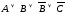 – элементарная дизъюнкция.
– элементарная дизъюнкция.
Элементарной
конъюнкцией (произведений)
называется конъюнкция (произведение)
логических переменных и их отрицаний.
Например,
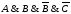 .
.
ТЕОРЕМА о тождественной истинности элемент. суммы: чтобы элементарная сумма была истинной, необходимо чтобы в ней содержалась хотя бы одна пара слагаемых, из которых одно есть некоторая переменная, а другое - ее отрицание.
ТЕОРЕМА о тождественной ложности элементарного произведения: чтобы элементарное произведение было тождественно ложным необходимо, чтобы в нем содержалось хотя бы одна пара множителей, из которых один является отрицанием другого.
-
КНФ и ДНФ. Преобразования формул алгебры высказываний к КНФ и ДНФ. Теорема о существовании КНФ и ДНФ формулы алгебры высказываний.
КНФ (конъюнктивная нормальная форма) - формула, представляющая собой произведение элементарных сумм (или конъюнкция элементарных дизъюнкций). пример: (X\/(¬X))&(Y\/Z\/W)
ДНФ (дизъюнктивная нормальная форма) - формула, представляющая собой сумму элементарных произведений (или дизъюнкцию элементарных конъюкций). пример: (X&(¬X))\/(Y&Z&W).
-
Критерии тождественной истинности и ложности формул алгебры высказываний.
Критерий тождественной истинности формулы
Для того, чтобы формула была тождественно истинной, необходимо и достаточно, чтобы каждый множитель ее КНФ имел по крайней мере два слагаемых, из которых одно является какой-нибудь переменной, а другое – ее отрицанием.
Критерий тождественной ложности формулы
Для того, чтобы формула была тождественно ложной, необходимо и достаточно, чтобы каждое слагаемое ее ДНФ имел по крайней мере два множителя, из которых один является какой-нибудь переменной, а другой – ее отрицанием.
-
СКНФ и СДНФ. Преобразование формул алгебры высказываний к СКНФ и СДНФ, используя равносильности алгебры высказываний.
Совершенной
ДНФ
(СДНФ) формулы
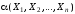 ,
содержащей
n
различных переменных, называется ДНФ,
обладающая следующими свойствами:
,
содержащей
n
различных переменных, называется ДНФ,
обладающая следующими свойствами:
-
в ней нет двух одинаковых слагаемых;
-
ни одно слагаемое не содержит двух одинаковых множителей;
-
никакое слагаемое не содержит переменной вместе с ее отрицанием;
-
в каждом слагаемом содержится в качестве множителей либо переменная
 ,
либо ее отрицание, где
,
либо ее отрицание, где
 .
.
Совершенной
КНФ
(СКНФ) формулы
 ,
содержащей n
различных переменных, называется КНФ,
обладающая следующими свойствами:
,
содержащей n
различных переменных, называется КНФ,
обладающая следующими свойствами:
-
в ней нет двух одинаковых множителей;
-
ни один множитель не содержит двух одинаковых слагаемых;
-
ни один множитель не содержит переменной вместе с ее отрицанием;
-
каждый множитель содержит в качестве слагаемого либо переменную
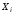 ,
либо ее отрицание, где
,
либо ее отрицание, где
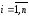 .
.
Алгоритм приведения к сднф:
-
Приводим формулу к ДНФ.
-
Если в конъюнкт входит переменная вместе со своим отрицанием, то этот конъюнкт удаляют из ДНФ.
-
Если в конъюнкт одна переменная входит несколько раз, то удаляют все такие переменные кроме одной.
-
Если в некоторый конъюнкт вида
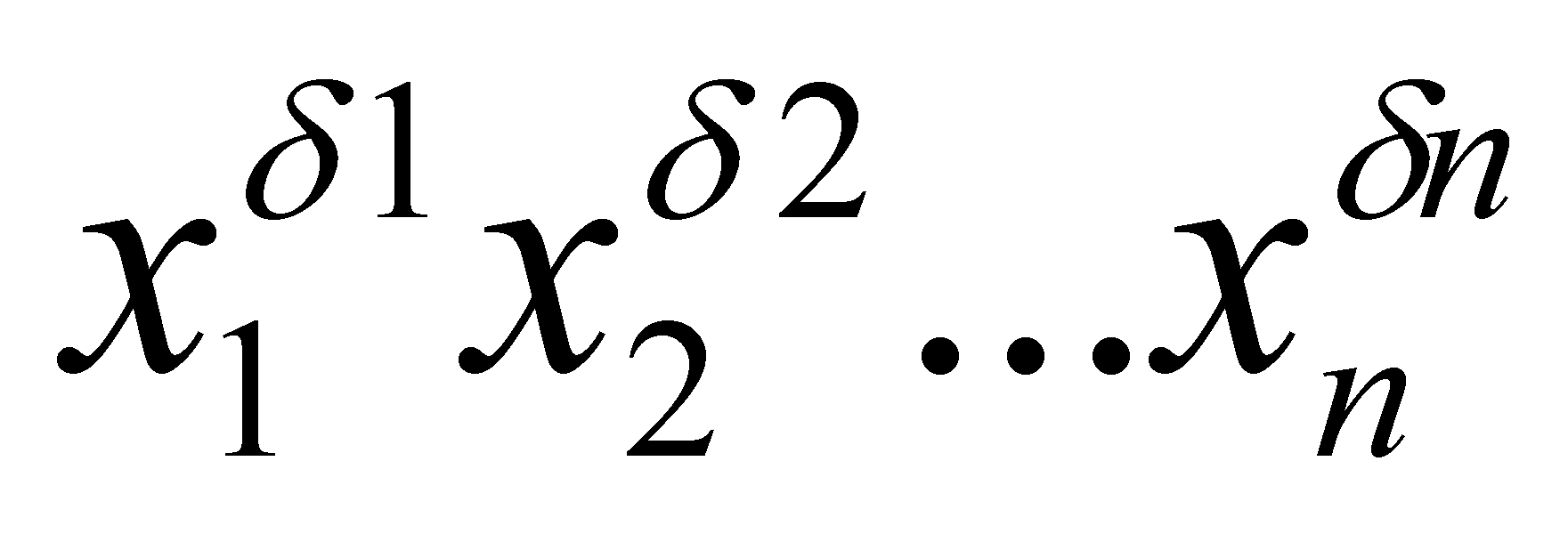 не
входит переменная y,
которая встречается в формуле, то его
заменяют конъюнктом вида
не
входит переменная y,
которая встречается в формуле, то его
заменяют конъюнктом вида  ,
затем, применяя дистрибутивность
конъюнкции относительно дизъюнкции
приводят формулу к ДНФ.
,
затем, применяя дистрибутивность
конъюнкции относительно дизъюнкции
приводят формулу к ДНФ. -
Если в полученной ДНФ имеется несколько одинаковых конституант единицы, то повторяющиеся конституанты удаляют, оставляя одну.
Аналогично построен алгоритм нахождения СКНФ.
-
СКНФ и СДНФ. Получение СКНФ и СДНФ формулы алгебры высказывания при помощи таблицы истинности.
Совершенной
ДНФ
(СДНФ) формулы
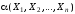 ,
содержащей
n
различных переменных, называется ДНФ,
обладающая следующими свойствами:
,
содержащей
n
различных переменных, называется ДНФ,
обладающая следующими свойствами:
-
в ней нет двух одинаковых слагаемых;
-
ни одно слагаемое не содержит двух одинаковых множителей;
-
никакое слагаемое не содержит переменной вместе с ее отрицанием;
-
в каждом слагаемом содержится в качестве множителей либо переменная
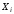 ,
либо ее отрицание, где
,
либо ее отрицание, где
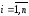 .
.
Совершенной
КНФ
(СКНФ) формулы
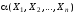 ,
содержащей n
различных переменных, называется КНФ,
обладающая следующими свойствами:
,
содержащей n
различных переменных, называется КНФ,
обладающая следующими свойствами:
-
в ней нет двух одинаковых множителей;
-
ни один множитель не содержит двух одинаковых слагаемых;
-
ни один множитель не содержит переменной вместе с ее отрицанием;
-
каждый множитель содержит в качестве слагаемого либо переменную
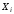 ,
либо ее отрицание, где
,
либо ее отрицание, где
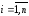 .
.
Для нахождения СДНФ по таблице истинности выбирают все встречающиеся в ней 1 и рассматривают наборы значений переменных, эквивалентные этим единицам. При этом СДНФ всегда содержит столько слагаемых, сколько единиц имеет таблица истинности. Переменная входит в конъюнкт без отрицания, если в таблице ей соответствует значение 1, иначе – 0.
Аналогично построен алгоритм нахождения СКНФ.
-
Описание исчисления высказываний (ИВ). Символы ИВ. Формулы ИВ. Элементарные формулы ИВ, части формул ИВ.
Исчисление высказываний это новая логическая система, которая адекватна алгебре высказываний, но здесь мы не будем рассматривать закон исключения третьего. Сами законы нас будут интересовать только в смысле выводимости. Т.е. мы будем себе ставить задачу обосновать тот или иной закон, показав, что пользование им не приведет к противоречию.
Символы исчисления высказываний состоят из знаков трех категорий.
-
Большие латинские буквы
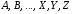 .
Эти символы мы будем называть переменными
высказываниями.
.
Эти символы мы будем называть переменными
высказываниями. -
Логические связки: & знак конъюнкции (или логического умножения);
 дизъюнкции
(или логического сложения);
дизъюнкции
(или логического сложения);
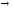 импликации
(или логического следования) и
импликации
(или логического следования) и
 знак отрицания.
знак отрицания. -
Скобки: ( ).
В исчислении высказываний определение формулы представляет собой следующую рекурсию:
-
Переменное высказывание есть формула.
-
Если
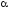 и
и
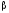 формулы, то слова
формулы, то слова
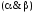 ,
,
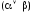 ,
,
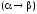 и
и
 также формулы.
также формулы.
Переменные высказывания называются также элементарными формулами.
Определение части формулы представляет собой следующую рекурсию:
-
Частью каждой элементарной формулы является только она сама.
-
Если определены все части формул
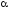 и
и
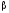 ,
то частями формулы (
,
то частями формулы (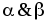 )
будут все части формул
)
будут все части формул
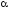 и
и
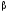 и сама формула. Аналогично определяются
части формул
и сама формула. Аналогично определяются
части формул
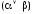 ,
,
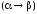 и
и
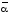 .
.
-
Выводимые формулы ИВ. Аксиомы ИВ.
В исчислении высказываний можно выделить некоторый класс формул, которые мы будем называть выводимыми в исчислении высказываний.
Правила, позволяющие из имеющихся выводимых формул получать новые, мы будем называть правилами вывода, а исходные выводимые формулы – аксиомами.
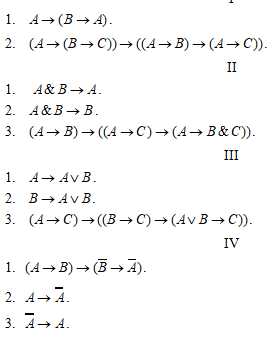
-
Правила вывода формул в ИВ (подстановки и заключения).
В ИВ можно выделить некоторый класс формул, которые мы будем называть выводимыми в ИВ. Правила, позволяющие из имеющихся выводимых формул получать новые, мы будем называть ПРАВИЛАМИ ВЫВОДА, а исходные выводимые формулы – аксиомами.
