27. Доверительные интервалы.

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Метод доверительных интервалов разработал американский статистик Ю. Нейман (Neyman J.), исходя из идей английского статистика Р. Фишера (Fisher R.).^{[ссылка 1]}

Определение

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100p%^{[примечание 1]}, порождённым выборкой (x₁,…,x_n), называется интервал с границами l(x₁,…,x_n) и u(x₁,…,x_n), которые являются реализациями случайных величин L(X₁,…,X_n) и U(X₁,…,X_n), таких, что

.

Граничные точки доверительного интервала l и u называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.^{[ссылка 2]}

[Править]Примеры

• Доверительный интервал для математического ожидания нормальной выборки;

• Доверительный интервал для дисперсии нормальной выборки.

28. Статистическая гипотеза. Статистический критерий. Уровень значимости и мощность критерия.

Статистическая гипотеза (statistical hypothesys) — это определённое предположение о распределении вероятностей, лежащем в основе наблюдаемой выборки данных.

Проверка статистической гипотезы (testing statistical hypotheses) — это процесс принятия решения о том, противоречит ли рассматриваемая статистическая гипотеза наблюдаемой выборке данных.

Статистический тест или статистический критерий — строгое математическое правило, по которому принимается или отвергаетсястатистическая гипотеза.

Методика проверки статистических гипотез

Пусть задана случайная выборка  — последовательность объектов из множества . Предполагается, что на множестве  существует некоторая неизвестная вероятностная мера .

Методика состоит в следующем.

1. Формулируется нулевая гипотеза 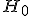 о распределении вероятностей на множестве 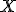. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая  и альтернативная . Иногда альтернатива не формулируется в явном виде; тогда предполагается, что  означает «не 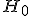». Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже.

2. Задаётся некоторая статистика (функция выборки) , для которой в условиях справедливости гипотезы 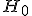 выводится функция распределения  и/или плотность распределения . Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика 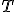. 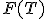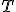Вывод функции распределения  при заданных  и  является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для ; в статистических пакетах имеются готовые вычислительные процедуры.

3. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число 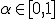. На практике часто полагают .

4. На множестве допустимых значений статистики  выделяется критическое множество  наименее вероятных значений статистики 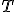, такое, что . Вычисление границ критического множества как функции от уровня значимости 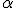 является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение.

5. Собственно статистический тест (статистический критерий) заключается в проверке условия:

• если , то делается вывод «данные противоречат нулевой гипотезе при уровне значимости ». Гипотеза отвергается.

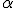• если , то делается вывод «данные не противоречат нулевой гипотезе при уровне значимости ». Гипотеза принимается.

Итак, статистический критерий определяется статистикой  и критическим множеством , которое зависит от уровня значимости .

Замечание. Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна. Тому есть две причины.

• По мере увеличения длины выборки нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия данных гипотезе, и она будет отвергнута. То есть многое зависит от объёма данных; если данных не хватает, можно принять даже самую неправдоподобную гипотезу.

• Выбранная статистика  может отражать не всю информацию, содержащуюся в гипотезе . В таком случае увеличивается вероятность ошибки второго рода — нулевая гипотеза может быть принята, хотя на самом деле она не верна. Допустим, например, что  = «распределение нормально»;  = «коэффициент асимметрии»; тогда выборка с любым симметричным распределением будет признана нормальной. Чтобы избегать таких ошибок, следует пользоваться более мощными критериями.