1. Дифференциальные уравнения 1 порядка. Основные понятия. Качественный анализ -огибающие, особые решения. Поле исправлений.

Уравнение

F(x, y, y ') = 0,

где y = y(x) — неизвестная, непрерывно дифференцируема на (a,b) функция, называется обыкновенным дифференциальным уравнением первого порядка.

 

Функция y = y(x) называется решением дифференциального уравнения F(x, y, y ') = 0, если она непрерывно дифференцируема на (a,b) и F(x, y(x), y '(x)) ≡ 0 для всех x из (a,b) .

 

График решения дифференциального уравнения называют интегральной кривой дифференциального уравнения.

 

Дифференциальное уравнение 1–го порядка имеет бесконечно много решений. Для того чтобы выделить единственное решение, нужно задать дополнительные (начальные) условия.

Задача отыскания решения y = y(x) уравнения F(x, y, y ' ) = 0 , удовлетворяющего условию y(x₀) = y₀, называется задачей Коши (или начальной задачей).

Условие y(x₀) = y₀ — начальное условие.

 

Любое конкретное решение y = y(x) (решение задачи Коши) уравнения 1–го порядка, называется частным решением уравнения.

 

Общее решение уравнения, записанное в неявной форме Φ(x, y) = C, называетсяобщим интегралом уравнения.

 

Частное решение уравнения, записанное в неявной форме Φ(x, y) = 0, называетсячастным интегралом уравнения.

 

Уравнение 1-го порядка, разрешенное относительно производной, называют уравнением, записанными в нормальной форме:

 

Уравнения первого порядка часто записывают в дифференциальной форме:

M(x, y)dx + N(x, y)dy = 0.

Решение такого уравнения можно искать как в виде y = y(x) , так и в виде x = x(y) .

2. Задача Коши. Теорема существования и единственности.

Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений(обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемымначальным условиям (начальным данным).

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t = 0, а решение отыскивается при t > 0.

От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.

Говорят, что задача Коши имеет единственное решение, если она имеет решение y =f(x) и никакое другое решение не отвечает интегральной кривой, которая в сколь угодно малой выколотой окрестности точки (x0,y0) имеет поле направлений, совпадающее с полем направлений y = f(x). Точка (x0,y0) задаёт начальные условия.

Различные постановки задачи Коши

ОДУ первого порядка, разрешённая относительно старшей производной

Система n ОДУ первого порядка, разрешённая относительно старших производных

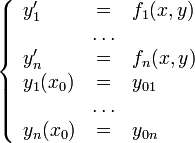
ОДУ n-го порядка, разрешённая относительно старшей производной

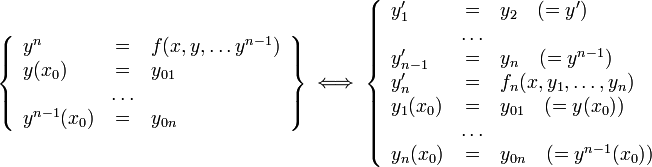
Теоремы о разрешимости задачи Коши

Пусть в области   рассматривается задача Коши:

y(x0) = y0,

где  . Пусть правая часть является непрерывной функцией в  . В этих предположениях имеет место теорема Пеано, устанавливающая локальную разрешимость задачи Коши: Пусть a>0 и b>0 таковы, что замкнутый прямоугольник

принадлежит области D, тогда на отрезке [x0 − α,x0 + α], где α = min{a,b / M},  , существует решение задачи Коши.

Указанный отрезок называется отрезком Пеано. Заметим, что, локальный характер теоремы Пеано не зависит от гладкости правой части. Например, для f(x,y) = y2 + 1 и для x0 = 0,y0 = 0 решение y(x) = tan(x) существует лишь на интервале ( − π,π). Также отметим, что без дополнительных предположений относительно гладкости правой части, нельзя гарантировать единственность решения задачи Коши. Например, для   возможно более одного решения.

Чтобы сформулировать теорему о единственности решения задачи Коши небоходимо наложить дополнительные ограничения на правую часть. Будем говорить, что функция f(x,y) удоволетворяет условию Липшица на D относительно y, если существует постоянная L такая, что

для всех  , i=1,2.

Пусть правая часть f(x,y) дополнительно удовлетворяет условию Липшица на D относительно y, тогда задача Коши не может иметь в D более одного решения.

Также отметим, что хотя эта теорема имеет глобальный характер, тем не менее она не устанавливает существование глобального решения.

Для существовования глобального решения необходимо наложить условия на рост правой части по y: пусть функция f удовлетворяет условию

где A>0 - константа не зависящая ни от x, ни от y, тогда задача Коши имеет решение в D. В частности, из этой теоремы следует, что задача Коши для линейных уравнений (с непрерывными по x коэффициентами) имеет глобальное решение.

Обыкновенное дифференциальное уравнение 1-го порядка в общем случае имеет вид .

 

Если его удаётся разрешить относительно  , то будем иметь УДО вида

 

.

Иная форма записи последнего .

Простейшим обыкновенным дифференциальным уравнением 1-го порядка является  , решение которого выглядит как , где   — производная постоянная, то есть уравнение имеет бесчисленное множество решений.

 

О: Задача нахождения решения обыкновенного дифференциального уравнения, которое удовлетворяет начальному условию   (такая запись эквивалентна ) именуется задачей Коши.

 

Т. (о существовании и единственности задачи Коши): Если функция  и её частная производная   непрерывны в окрестности т.  , то в окрестностях т. имеется единственное решение   задачи Коши  ■

 

О: Общим решением обыкновенного дифференциального уравнения 1-го порядка называется функция  , которая удовлетворяет следующим условиям:

 

функция  является решением  ;

при любом начальном условии , имеется такое значение  , при котором   удовлетворяет имеющемуся начальному условию. Точка   — области, где выполняются условия существования и единственности решения.

Пример:  — общее решение обыкновенного дифференциального уравнения. Пользуясь начальным условием  , определяем  , то есть — решение задачи Коши в области

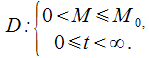
Примечание: Иногда общее решение обыкновенного дифференциального уравнения существует в неявном виде , тогда оно именуется общим интегралом.