21. Основные законы распределения случайной величины. Равномерное биноминальное распределение пуассона показательное . Нормальный закон распределения.

Основные законы распределения целочисленных случайных величин

Определение целочисленной случайной величины. Производящая функции и её свойства. Биномиальный, пуассоновский, геометрический и равномерный законы распределения, производящие функции для этих законов распределения и их числовые характеристики. Гипергеометрический закон распределения.

Производящие функции

Среди дискретных случайных величин особенно важны величины, принимающие только целые значения 0, 1, 2, … Такие случайные величины называются целочисленными. Для изучения таких величин вводится понятие производящей функции. Пусть – целочисленная случайная величина с распределением вероятности 

Функция комплексного аргумента 

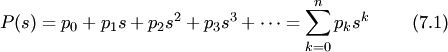
называется производящей функцией данного распределения. Ряд (7.1) сходится по крайней мере в единичном круге . Укажем основные свойства производящей функции.

Свойство 1. .

Свойство 2. Математическое ожидание случайной величины выражается формулой

Свойство 3. Дисперсия случайной величины выражается формулой

Таким образом, производящую функцию можно использовать для нахождения числовых характеристик целочисленных случайных величин. Более того, она полностью задаёт закон распределения этих величин.

Рассмотрим наиболее часто встречающиеся законы распределения целочисленных случайных величин.

Биномиальный закон (распределение Бернулли)

В общей форме биномиальный закон описывает осуществление признака в  испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей  белых и  чёрных шаров. Если  — число появления белых шаров в выборке из  шаров, то

где  — вероятность появления при одном извлечении соответственно белого и чёрного,

Производящая функция биномиального распределения задаётся формулой

Основные характеристики биномиального распределения (математическое ожидание и дисперсия):

Закон распределения Пуассона (закон редких событий)

Случайная величина  называется распределённой по закону Пуассона с параметром , если

Производящая функции распределения Пуассона задаётся формулой

Характерной особенностью распределения Пуассона являются совпадения математического ожидания и дисперсии, причём

Распределение Пуассона можно получить из биномиального распределения путёмпредельного перехода при  при условии  и в этом случае интерпретируется как закон “редких” явлений. Если  достаточно велико, a  мало, то формулу Пуассона (7.3) часто используют в качестве приближения вместо точных биномиальных формул для вероятностей  успехов в  испытаниях (подробнее см. часть 3).

Геометрический закон распределения

Последовательно проводится несколько независимых испытаний до появления некоторого события , вероятность которого в каждом испытании одна и та же и равна . Тогда число  произведённых испытаний есть дискретная случайная величина с геометрическим распределением вероятности. Примером может служить стрельба по некоторой цели до первого попадания, причём вероятность попадания при каждом выстреле не зависит от результатов предыдущих выстрелов и сохраняет постоянное значение . Число  произведённых выстрелов будет случайной величиной, возможные значения которой являются все натуральные числа. Геометрический закон распределения задаётся формулой

 где 

Характеристическая функция геометрического закона распределения задаётся формулой

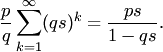
Основные характеристики геометрического закона распределения (математическое ожидание и дисперсия):

Равномерный закон распределения

Равномерное распределение задаётся следующим законом:

Этот закон имеет место в случае, когда  возможных исходов испытания равновероятны. Примером целочисленной случайной величины, распределённой по равномерному закону, может служить число очков, выпадающих при бросании симметричной кости (любое из значений  выпадает с одинаковой вероятностью ). Характеристическая функция равномерного закона задаётся формулой

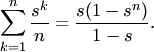
Числовые характеристики геометрического закона распределения (математическое ожидание и дисперсия):

Гипергеометрический закон распределения

Основные законы распределения непрерывных случайных величин

Определение характеристической функции и её использование в теории вероятностей. Нормальный закон распределения и его значение в теории вероятностей. Логарифмически нормальный закон. Гамма-распределение. Экспоненциальный закон и его использование в теории надёжности, теории очередей. Равномерный закон. Распределения хи-квадрат, Вейбула, Стьюдента, Фишера.

Характеристическая функция

Во многих задачах полезной характеристикой случайной величины является её характеристическая функция. Характеристической функцией случайной величины  называется математическое ожидание комплексной случайной величины , рассматриваемое как функции параметра  (здесь и далее в этой части – мнимая единица). Таким образом, характеристичская функция непрерывной случайной величины  задаётся формулой

, где – плотность вероятности.

Отметим следующие свойства характеристической функции:

1) при любом действительном значении  характеристическая функция по модулю не превосходит единицы, то есть

2) характеристическая функция равна единицы при , то есть .

Плотность вероятности случайной величины  можно выразить через её характеристическую функцию:

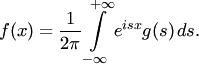
Таким образом, характеристическая функция случайной величины является её полной вероятностной характеристикой. Зная характеристическую функцию случайной величины, можно найти её плотность вероятности, а следовательно, и функцию распределения, то есть полностью определить закон распределения случайной величины. Через характеристическую функцию можно выразить также числовые характеристики случайной величины, в частности её математическое ожидание и дисперсию:

Нормальный закон распределения (закон Гаусса)

Плотность вероятности нормально распределённой случайной величины  выражается формулой

(8.1)

Кривая распределения изображена на рис. 16. Она симметрична относительно точки (точка максимума). При уменьшении  ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис. 17).

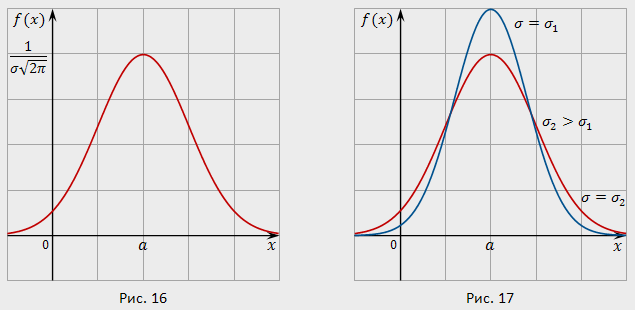
Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения (подробнее об этом [url]см. часть 9[/url]). Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия):

Таким образом, параметры  и  в выражении (8.1) нормального закона распределения представляют собой математическое ожидание и среднее квадратическое отклонение случайной величины. Принимая это во внимание, формулу (8.1) можно представить следующим образом:

Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину. Разумеется, что в общем случае, когда характер закона распределения неизвестен, знание математического ожидания и дисперсии недостаточно для определения этого закона распределения.

Характеристическая функция нормального распределения случайной величины задаётся формулой

Логарифмически нормальное распределение

Говорят, что случайная величина  имеет логарифмически нормальное распределение (сокращённо логнормальное распределение), если её логарифм  распределён нормально, то есть если

где величина  имеет нормальное распределение с параметрами 

Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин:

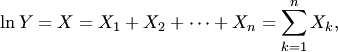 то есть 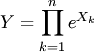, где  независимы.

Гамма-распределение

Экспоненциальный закон распределения

Экспоненциальным распределением называется частный случай гамма-распределения с параметрами , то есть то есть плотность вероятности в этом случае

Используя свойства два плотности распределения ([url]см.[/url]), можно найти функцию распределения  экспоненциального закона:

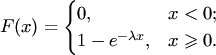
Основные характеристики (математическое ожидание и дисперсия) случайной величины , распределённой по экспоненциальному, имеют вид

Характеристическая функция экспоненциального распределения задаётся формулой

Кривая экспоненциального распределения вероятностей показана на рис. 21а, а график функции распределения  — на рис. 21б.

Статистический смысл параметра  состоит в следующем:  есть среднее число событий на единицу времени, то есть  есть средний промежуток времени между двумя последовательными событиями.

Экспоненциальное (показательное) распределение часто встречается в теории массового обслуживания (например,  — время ожидания при техническом обслуживании или  — продолжительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и теории надёжности (например,  — срок службы радиоэлектронной аппаратуры).

Пример 2. Случайная величина  — время работы радиолампы — имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 ч, если среднее время работы радиолампы 400 ч.

Решение. По условию задачи математическое ожидание случайной величины  равно 400 ч, следовательно, . Искомая вероятность есть

Распределение Вейбула

Равномерный закон распределения

Случайная величина  называется распределённой равномерно на отрезке , если её плотность распределения вероятностей постоянна на данном отрезке:

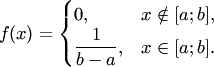
Все возможные значения равномерно распределённой случайной величины лежат в пределах некоторого интервала; кроме того. в пределах этого интервала все значения случайной величины одинаково вероятны (обладаю одной и той же плотностью вероятности). Равномерно распределение реализуется в экспериментах, где наудачу ставиться точка на отрезке  ( — абсцисса поставленной точки). Равномерно распределённая случайная величина встречается также в измерительной практике при округлении отчётов измерительных приборов до целых делений шкал. Ошибка при округлении отчёте до ближайшего целого деления является случайной величиной , которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями.

Математическое ожидание и дисперсия равномерно распределённой случайной величины

Характеристическая функция равномерного распределения задаётся формулой

График плотности равномерного распределения изображён на рис. 23.

Пример 3. Найти вероятность попадания случайной величины, имеющей равномерное распределение на отрезке , на участок , представляющий собой часть отрезка .

Решение. Используя свойство 3 плотности вероятности, получаем

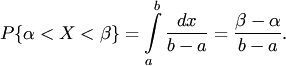
Распределение хи-квадрат 

Распределение Стьюдента

Распределение Фишера