
- •Розділ iіі Відношення
- •3.1. Основні поняття та властивості відношень
- •3.1.1. Основні означення.
- •3.1.2. Подання бінарних відношень за допомогою матриці та графа.
- •3.1.3. Композиція відношень.
- •3.1.4. Подання композиції відношень матрицями та графами.
- •3.1.5. Властивості відношень.
- •3.1.6. Багатомісні відношення. Зв’язок відношень з реляційними базами даних.
- •3.2. Функціональне відношення.
- •3.2.1. Відображення.
- •3.2.2. Типи відображень.
- •3.2.3. Композиція відображень.
- •3.2.4. Суперпозиція функцій.
- •3.3. Відношення еквівалентності
- •3.3.1. Означення відношення еквівалентності. Загальні відомості.
- •3.3.2. Матриця і граф відношення еквівалентності.
- •3.4. Відношення порядку.
- •3.4.1. Загальні властивості.
- •3.4.2. Вагові функції.
- •3.4.3. Квазіпорядок.
- •3.4.4. Структура впорядкованих множин.
- •3.4.5. Матриці відношень порядку.
- •Контрольні запитання.
Розділ iіі Відношення
3.1. Основні поняття та властивості відношень
3.1.1. Основні означення.
Ми вже
знаємо, що за Н. Бурбакі
елементи множини можуть знаходитися в
деяких відношеннях між собою або з
елементами інших множин, але означення
відношення не давалося. Загалом відношення
означає який-небудь зв'язок між предметами
або поняттями. Унарні (одномісні)
відношення віддзеркалюють наявність
деякої певної властивості (ознаки) у
елементів множини (наприклад, «бути
фахівцем» в множині співробітників
фірми). У цьому випадку всі елементи
![]() з цієї множини
з цієї множини
![]() ,
які мають цю властивість (ознаку)
,
які мають цю властивість (ознаку)
![]() ,
утворюють деяку підмножину множини
,
утворюють деяку підмножину множини
![]() ,
яке називається унарним відношенням
,
яке називається унарним відношенням
![]() ,
тобто
,
тобто
![]() .
Відношення між парами об'єктів називаються
бінарними
(двомісними). Звичайно відношення
записується у вигляді співвідношень
.
Відношення між парами об'єктів називаються
бінарними
(двомісними). Звичайно відношення
записується у вигляді співвідношень
![]() ,
де
,
де
![]() – відношення, яке встановлює зв'язок
між елементом
– відношення, яке встановлює зв'язок
між елементом
![]() і елементом
і елементом
![]() .
.
Приклад 3.1. Приклади бінарних відношень:
1. входити до складу деякого колективу;
2. відношення належності;
3. включення множин;
4. працювати в одній фірмі;
5. нерівність чисел;
6. бути братом;
7. ділитися на яке-небудь натуральне число.
Для наведених відношень запишемо відповідні їм співвідношення:
1. Розов – староста групи 1ЕК;
2.·Коцар і Степаненко вчаться в одній групі;
3.·![]() ;
;
4. Резнік і Тимошенко працюють в одній фірмі;
5.
![]() ;
;
6. Богдан брат Віктора;
7. 6 ділиться на 3.
Бінарне
відношення повністю визначається
множиною всіх пар елементів
![]() ,
для яких воно справджується. Тому
будь-яке бінарне відношення можна
розглядати як множину впорядкованих
пар
,
для яких воно справджується. Тому
будь-яке бінарне відношення можна
розглядати як множину впорядкованих
пар
![]() ,
тобто можна дати таке строго математичне
означення бінарного відношення.
,
тобто можна дати таке строго математичне
означення бінарного відношення.
Означення
3.1.
Бінарним
відношенням
![]() ,
що діє з множини
,
що діє з множини
![]() у множину
у множину
![]() ,
називається деяка підмножина декартова
добутку множин
,
називається деяка підмножина декартова
добутку множин
![]() і
і
![]()
![]() ,
тобто
,
тобто
![]() .
.
Приклад
3.2.
Нехай
множина
![]() Стеценко,
Чуйко, Козак}, є деякою множиною прізвищ,
а множина
Стеценко,
Чуйко, Козак}, є деякою множиною прізвищ,
а множина
![]() старший
менеджер, менеджер} є множиною посад
філії деякої фірми. Декартів добуток
старший
менеджер, менеджер} є множиною посад
філії деякої фірми. Декартів добуток
![]() містить 6 впорядкованих пар. Це пари
містить 6 впорядкованих пар. Це пари
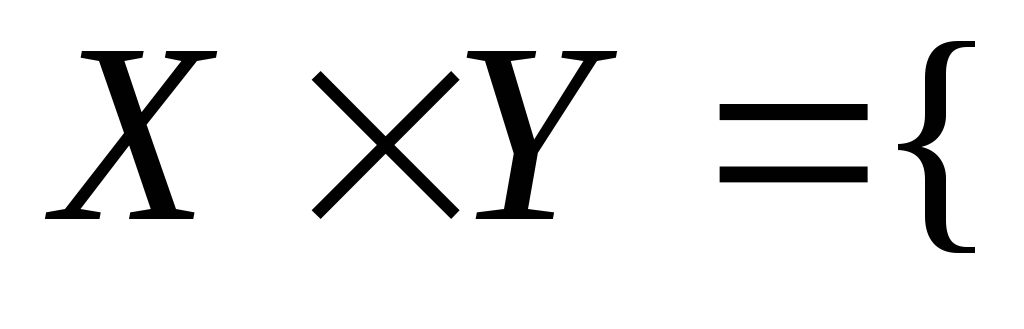 (Стеценко,
старший менеджер), (Стеценко, менеджер),
(Чуйко, старший менеджер), (Чуйко,
менеджер), (Козак, старший менеджер),
(Козак, менеджер)}.
Розглянемо бінарне відношення
(Стеценко,
старший менеджер), (Стеценко, менеджер),
(Чуйко, старший менеджер), (Чуйко,
менеджер), (Козак, старший менеджер),
(Козак, менеджер)}.
Розглянемо бінарне відношення
![]() ,
де
,
де
![]() (Чуйко,
старший менеджер), (Стеценко, менеджер),
(Козак, менеджер)}.
Це відношення встановлює відповідність
прізвищ осіб посадам, які вони займають
у філії фірми, тобто є відношенням
„займати посаду”.
(Чуйко,
старший менеджер), (Стеценко, менеджер),
(Козак, менеджер)}.
Це відношення встановлює відповідність
прізвищ осіб посадам, які вони займають
у філії фірми, тобто є відношенням
„займати посаду”.
Бінарне
відношення встановлює відповідність
елементів множини
![]() елементам множини
елементам множини
![]() .
Зрозуміло, що співвідношення
.
Зрозуміло, що співвідношення
![]() можна записати у вигляді
можна записати у вигляді
![]() ,
де
,
де
![]() .
Наприклад, Чуйко займає посаду старшого
менеджера еквівалентно (Чуйко, старший
менеджер)
.
Наприклад, Чуйко займає посаду старшого
менеджера еквівалентно (Чуйко, старший
менеджер)
![]() „займати посаду”,
„займати посаду”,
![]() еквівалентно
еквівалентно
![]() (але не можна записати
(але не можна записати
![]() ).
Елемент
).
Елемент
![]() називають першою координатою, а елемент
називають першою координатою, а елемент
![]() – другою координатою впорядкованої
пари
– другою координатою впорядкованої
пари
![]() .
Множина перших координат називається
областю визначення (лівою областю)
відношення
.
Множина перших координат називається
областю визначення (лівою областю)
відношення
![]() і позначається
і позначається
![]() .
.
Множина
других координат називається областю
значень (правою областю) відношення
![]() і позначається
і позначається
![]() .
Якщо
.
Якщо
![]() ,
,
![]() ,
тоді
,
тоді
![]() ,
,
![]() .
У таких випадках кажуть, що
.
У таких випадках кажуть, що
![]() є відношенням від
є відношенням від
![]() до
до
![]() ,
що воно ставить у відповідність елементам
множини
,
що воно ставить у відповідність елементам
множини
![]() елементи множини
елементи множини
![]() ,
тому таке відношення (див. рис.3.1) називають
також відповідністю та позначають
,
тому таке відношення (див. рис.3.1) називають
також відповідністю та позначають
![]() .
Якщо
.
Якщо
![]() ,
то будь-яке відношення
,
то будь-яке відношення
![]() :
:
![]() є підмножиною
є підмножиною
![]() і називається відношенням в
і називається відношенням в
![]() .
Тобто в цьому випадку відношення
.
Тобто в цьому випадку відношення
![]() ставить у відповідність елементу множини
ставить у відповідність елементу множини
![]() елемент множини
елемент множини
![]() (рис.3.2).
(рис.3.2).

Рис.3.1
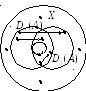
Рис.3.2
Якщо
![]() ,
то кажуть, що відношення
,
то кажуть, що відношення
![]() задано на
задано на
![]() .
.
Приклад 3.3.
Надано
дві множини
![]() ,
,
![]() .
.
Нехай
![]() – відношення «бути дільником» від
– відношення «бути дільником» від
![]() до
до
![]() .
Тоді
.
Тоді
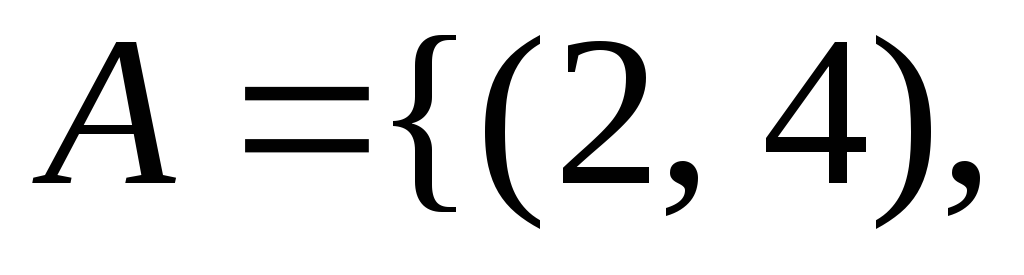
![]() .
Відношення
.
Відношення
![]() – « = » від
– « = » від
![]() до
до
![]() :
:
![]() ;
відношення
;
відношення
![]() – «>» від
– «>» від
![]() до
до
![]() :
:
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Відокремлюють
такі випадки відношень в
![]() :
:
1. Повне
(універсальне) відношення
![]() ,
яке справджується для будь-якої пари
,
яке справджується для будь-якої пари
![]() елементів з
елементів з
![]() ,
тобто
,
тобто
![]() .
Наприклад,
.
Наприклад,
![]() – відношення «вчитися в одній групі»
у множині
– відношення «вчитися в одній групі»
у множині
![]() ,
де
,
де
![]() – множина студентів групи 1ЕК.
– множина студентів групи 1ЕК.
2. Тотожне
(діагональне) відношення
![]() ,
що виконується тільки між елементом і
ним самим. Наприклад, рівність на множині
дійсних чисел.
,
що виконується тільки між елементом і
ним самим. Наприклад, рівність на множині
дійсних чисел.
3. Порожнє
відношення, якому не задовольняє жодна
пара елементів з
![]() ,
тобто
,
тобто
![]() .
Наприклад,
.
Наприклад,
![]() – відношення «бути братом» у множині
– відношення «бути братом» у множині
![]() ,
де
,
де
![]() – множина жінок.
– множина жінок.
Повне
і порожнє відношення можна визначити
і для випадку відношень від
![]() до
до
![]() .
Повним відношенням буде
.
Повним відношенням буде
![]() ,
яке справджується для будь якої пари
,
яке справджується для будь якої пари
![]() ,
де
,
де
![]() .
.
Порожнім
відношенням є відношення, якому не
задовольняє жодна пара елементів
![]() ,
де
,
де
![]() .
.
Означення
3.2.
Розглянемо
відношення
![]() .
Нехай елемент
.
Нехай елемент
![]() .
Перерізом відношення
.
Перерізом відношення
![]() за елементом
за елементом
![]() називається множина елементів
називається множина елементів
![]() з
з
![]() ,
для яких пара
,
для яких пара![]() .
.
Множину
всіх перерізів відношення
![]() називають фактором-множиною множини
називають фактором-множиною множини
![]() за відношенням
за відношенням
![]() і позначають
і позначають
![]() .
Вона повністю визначає відношення
.
Вона повністю визначає відношення
![]() .
.
Приклад 3.4.
![]() ,
,
![]() .
Відношення
.
Відношення
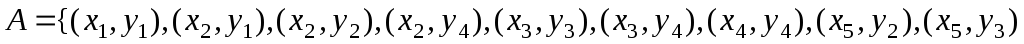 ,
,
![]() .
.
Випишемо
перерізи за всіма елементами множини
![]() у такому вигляді:
у такому вигляді:
|
Таблиця 3.1 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
Об'єднання
множин другого рядка утворять
фактор-множину
![]() .
.
