3. Элементарные преобразования матриц. Приведение матрицы к ступенчатому виду с помощью элементарных преобразований. Метод Гаусса.

3.1. Элементарные преобразования. Будем называть элементарным преобразованием типа I перестановку двух строк матрицы.

Элементарным преобразованием типа II будем называть следующую операцию: все строки матрицы, кроме одной, остаются прежними, но к этой одной строке прибавляется другая (любая), умноженная на некоторое число.

Утверждение 1. Преобразование, обратное к элементарному, является элементарным, т.е. если матрица В получена из матрицы А с помощью элементарного преобразования, то и матрица А может быть получена из матрицы В с помощью элементарного преобразования. Доказательство очевидно.

Утверждение 2. Пусть - расширенная матрица системы линейных уравнений. Элементарные преобразования этой матрицы не меняют множества решений системы.

Доказательство. Пусть - матрица, получившаяся из с помощью элементарного преобразования и пусть - решение исходной системы. Этот же набор чисел будет являться и решением системы с матрицей - в каждом из двух возможных случаев это очевидно. Значит, решений меньше не стало. А так как обратный переход от к осуществляется тоже с помощью элементарного преобразования, то каждое решение системы с матрицей будет решением системы с матрицей . Утверждение доказано.

3.2. Приведение матрицы к ступенчатому виду. С помощью элементарных преобразований можно перейти от исходной матрицы к матрице более простого вида. Алгоритм следующий: Пусть дана матрица

Рассмотрим первый столбец. Пусть в нем есть хотя бы один ненулевой элемент (если такого нет, перейдем ко второму столбцу). Поставим строку, где находится этот элемент, на первое место (элементарное преобразование первого типа). Теперь прибавим ко 2-й строке 1-ю, умноженную на подходящий коэффициент , подобрав его так, чтобы элемент стал равен 0: . Так же поступим с остальными строками: к -й строке прибавим 1-ю, умноженную на коэффициент Получим матрицу вида

Теперь на время забудем о первой строке. Повторим описанную процедуру для матрицы из элементов , . Если во втором столбце, начиная со второй строки, нет ненулевых элементов, перейдем к третьему столбцу. Если же есть ненулевой элемент, поставим его на вторую строку, поменяв строки местами. Затем к остальным строкам, начиная с третьей, прибавим вторую, умноженную на подходящий коэффициент так, чтобы элемент из второго столбца стал равен 0. Матрица примет вид:

.

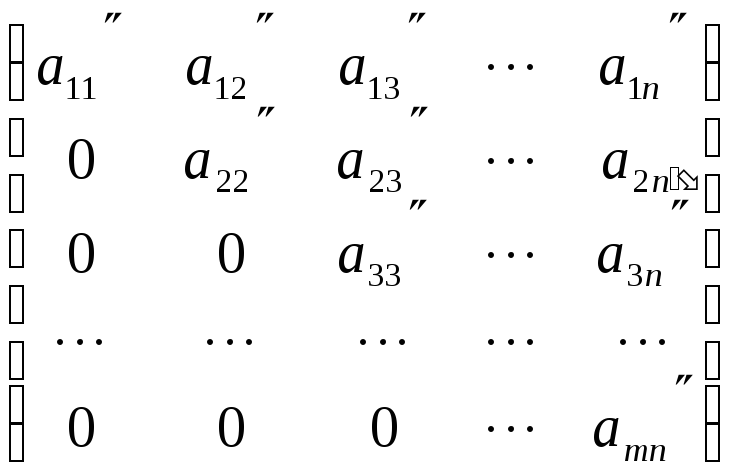Таким способом за конечное число шагов из любой матрицы мы получим матрицу следующего вида:

.

Такую матрицу называют ступенчатой (трапецевидной, квазитреугольной). В углу каждой ступеньки стоит ненулевой элемент.

4. Обратная матрица. Матричные уравнения.

4.1. Определение обратной матрицы. Мы по-прежнему будем рассматривать квадратные матрицы.

Определение. Пусть дана матрица А. Назовем матрицу правой обратной для А, если (– единичная матрица соответствующего порядка).

Аналогично, назовем левой обратной для А, если выполняется равенство .

Утверждение 1. .

Доказательство. Действительно,

Значит, можно говорить просто об обратной матрице. Будем ее обозначать А^-1. Итак,

.

Заметим, что не каждая матрица имеет обратную. Так как , то , и если (такие матрицы называются вырожденными), то матрица А не может иметь обратной матрицы.

Утверждение 2. Если обратная матрица существует, то она единственна. Иначе, если АВ = ВА = Е и АС = СА = Е, то В = С.

Доказательство:

4.2. Существование обратной матрицы. Мы уже заметили, что если определитель матрицы равен нулю, то она не имеет обратной. Оказывается, что если определитель матрицы не равен нулю, то она имеет обратную матрицу. Мы сейчас ее построим.

Составим сначала матрицу из алгебраических дополнений:

.

Затем транспонируем эту матрицу:

.

Получившаяся матрица называется присоединенной. Умножим на :

,

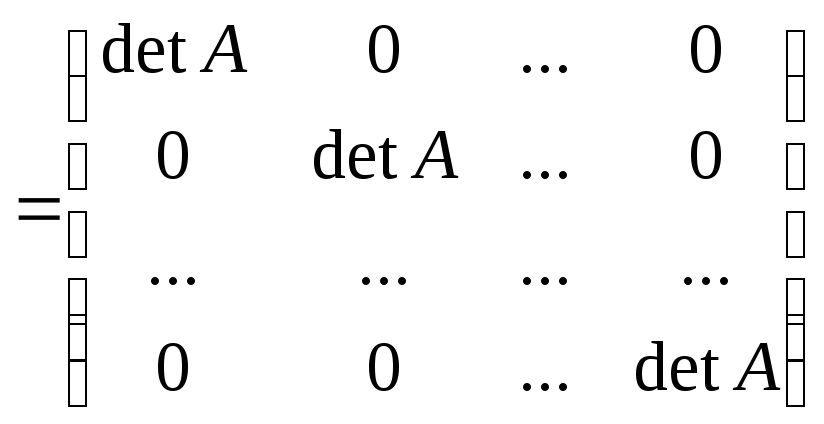так как

. Тогда .

4.3. Матричные уравнения. Умея находить обратные матрицы, можно решать матричные уравнения. Например, чтобы решить уравнение АХ = В, где А и В - квадратные матрицы одинакового размера, причем А – невырожденная, достаточно умножить обе части равенства слева на А^-1:

Аналогично, решением матричного уравнения ХА = В будет являться матрица Х = ВА^-1.

4.4. Решение систем линейных уравнений с помощью обратной матрицы. Пусть дана система линейных уравнений с квадратной матрицей, т.е. количество уравнений равно количеству неизвестных. В матричном виде эту систему можно записать . Если матрица А невырождена, т.е. ее определитель не равен нулю, то существует обратная матрица А^-1, и тогда

Мы получили решение такой системы линейных уравнений с помощью обратной матрицы и заодно показали единственность решения такой системы.

3.3. Метод Гаусса решения систем линейных уравнений (метод последовательного исключения переменных). Пусть дана система линейных уравнений

(*)

Составим расширенную матрицу системы (*):

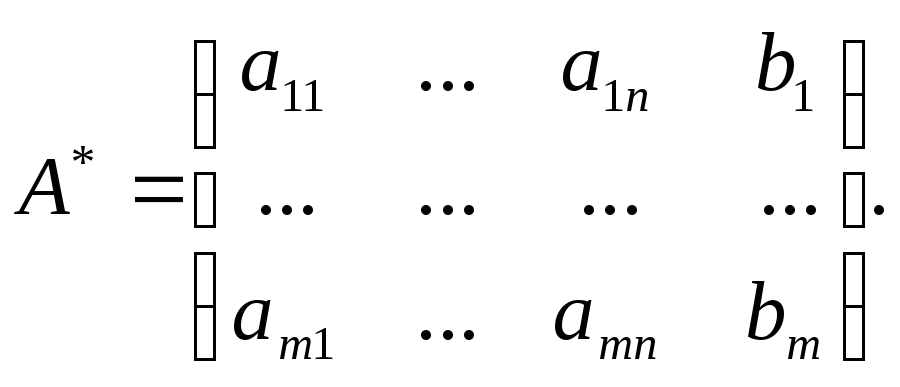
С помощью элементарных преобразований из мы можем получить другую матрицу, соответствующую другой системе уравнений, но, напомним, множество решений получившейся системы будет совпадать с множеством решений исходной системы (утверждение 2). Значит, если привести матрицу к ступенчатому виду, множество решений не изменится:

Тогда соответствующая система линейных уравнений выглядит так:

(**)

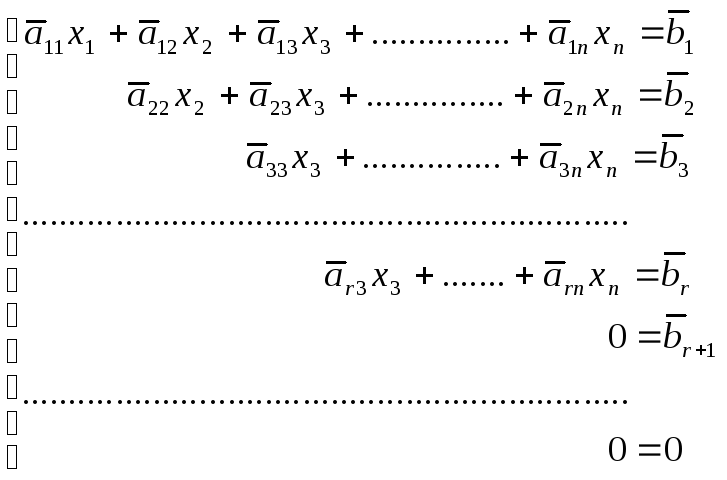Очевидно, что если в матрице оказалась строка причем то система уравнений несовместна.

Пусть таких строк нет. Тогда неизвестные назовем главными (они соответствуют нашим «ступенькам»). Количество главных неизвестных равно . Остальные неизвестные назовем свободными. Очевидно, их .

Для удобства записи будем считать, что главными оказались переменные , а свободными - (в конце концов, всегда можно переобозначить неизвестные величины). Расширенная матрица системы имеет вид:

,

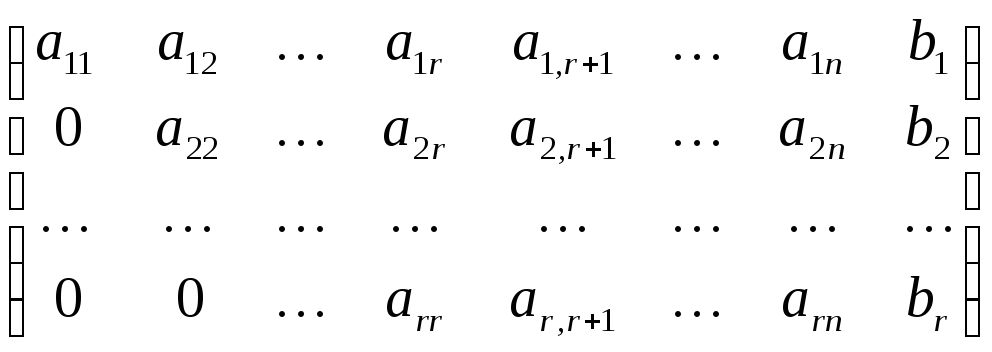причем .

До сих пор мы двигались сверху вниз – это был так называемый прямой ход метода Гаусса. Теперь начнем движение снизу вверх – обратный ход. Прибавим к -й строке -ю, умноженную на подходящий коэффициент , чтобы элемент стал равен нулю. Этот коэффициент нетрудно найти: . То же самое сделаем с остальными строками. (Заметьте: эти преобразования изменяют только элементы, стоящие в столбцах с номерами от до ). Теперь в -м столбце только элемент не равен нулю.

Поднимемся на строку выше. Так как , то можно добиться того, чтобы все элементы в -м столбце, кроме самого элемента , были равны нулю. Постепенно мы дойдем до первой строки и получим матрицу вида

.

Вспомним, что за каждой строкой матрицы стоит линейное уравнение:

Из этих уравнений сразу получаем выражения для главных неизвестных:

(***)

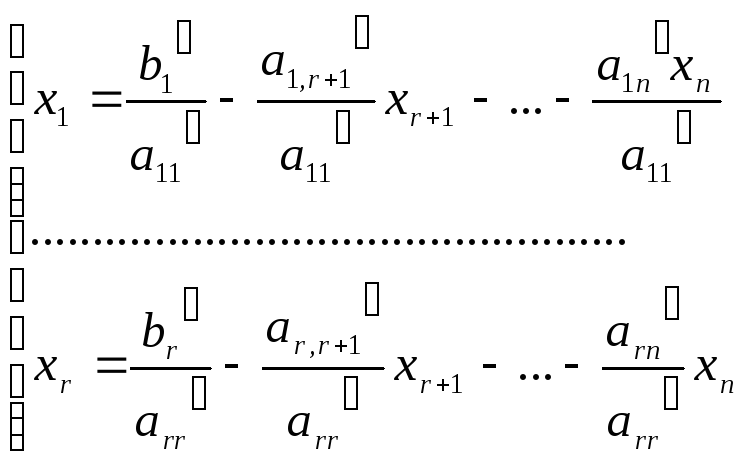Придадим свободным неизвестным произвольные значения. Тогда значения главных неизвестных будут определяться однозначно. Система (***) описывает все решения исходной системы (*).

Сформулируем некоторые, теперь уже очевидные, утверждения.

1. Система (*) совместна в получившейся ступенчатой системе (**) нет уравнений вида , где .

2. Совместная система является определенной в ступенчатой системе (**) .

3. Однородная система нетривиально совместна (т.е. имеет ненулевое решение) <.

Метод Гаусса решения систем линейных уравнений весьма удобен для небольших систем с небольшим количеством неизвестных.. Но в практических задачах, когда коэффициенты при неизвестных даны с определенной точностью и с определенной точностью ищутся решения, при использовании этого метода возникают некоторые проблемы, но это уже вопросы, которые излагаются в курсе «Численные методы».

Пока мы только описали множество решений системы линейных уравнений. О структуре этого множества мы поговорим позднее, когда будет введено понятие линейного пространства и линейной зависимости.

4.5. Правило Крамера в простейшем случае. Пусть дана система из двух линейных уравнений с двумя неизвестными:

Умножим первое уравнение на , а второе - на :

Вычитая из первого уравнения второе, получим выражение для неизвестной :

откуда, если ,

.

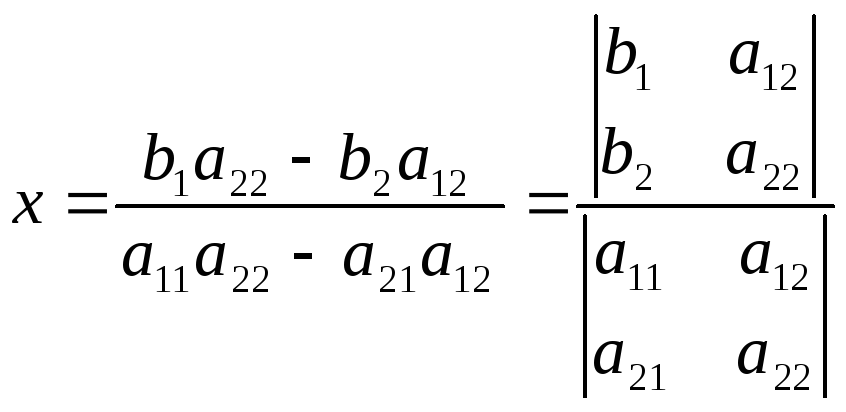Аналогично получается выражение для :

.

Заметим, что в знаменателе обоих выражений стоит определитель матрицы коэффициентов, а в числителе – определитель, получившийся из матрицы коэффициентов заменой соответствующего столбца на столбец правых частей.

Оказывается, этот симпатичный результат можно обобщить на случай произвольного числа уравнений . Напомним, речь идет только о системах линейных уравнений с квадратными матрицами коэффициентов.

4.6. Правило Крамера в общем случае. Пусть АХ = В - система линейных уравнений с квадратной матрицей коэффициентов, причем определитель матрицы не равен нулю. Тогда решением такой системы являются значения неизвестных

где , а - определитель матрицы, получившейся из матрицы заменой -го столбца на столбец правых частей.

Покажем, что набор чисел действительно является решением системы.

Так как матрица А невырождена, то существует обратная матрица А^-1. Умножим обе части равенства АХ = В слева на А^-1, получим

.

Заметим, что -я компонента получившегося вектор-столбца - это разложение определителя по -му столбцу. Значит,

.

Несмотря на привлекательность формулировки, практическое значение правила Крамера невелико: чтобы найти решение системы с неизвестными, приходится вычислять определитель -го порядка. Это оправдано при или .