2.1. Определитель матрицы 2х2.

Рассмотрим теперь систему двух линейных уравнений с двумя неизвестными:

(*)

Коэффициенты при неизвестных и для удобства обозначений имеют два индекса, первый из которых указывает, какому уравнению принадлежит коэффициент, а второй – при каком неизвестном он стоит. Таблица

,

составленная из коэффициентов при неизвестных, называется матрицей системы.

Исключим из этой системы неизвестное . Для этого умножим первое уравнение системы на , а второе – на , затем вычтем из первого уравнения второе. Получим

. (**)

Аналогично исключаем : . (***)

Если , то, разделив обе части уравнений (**) и (***) на , получим единственное решение системы (*):

, (****).

Числитель и знаменатель полученных выражений называют определителями или детерминантами второго порядка. Таким образом,

Определение. Назовем определителем или детерминантом 2-го порядка матрицы

число, равное . Обозначения: ==.

Об этом определителе говорят, что он соответствует матрице , и называют определителем системы (*). Числа называют элементами определителя (как и матрицы). Элементы образуют так называемую главную диагональ, а элементы - побочную.

Согласно этому определению формулы (****) принимают следующий вид:

, (*****).

Заметим, что определители и получаются из из определителя системы при помощи замены соответственно его первого и второго столбца столбцом свободных членов системы (*). Формулы (*****) называтся формулами Крамера.

Таким образом, если определитель (*) системы не равен нулю, то формулы Крамера дают единственное решение этой системы.

Рассмотрим другие случаи. Если определитель , но покрайней мере один из определителей или отличен от нуля, то система (*) не имеет решений (несовместна), так как покрайней мере одно из уравнений (**) или (***) является не возможным. Если , то система (*) имеет бесконечно много решений, так как или , следовательно, уравнения пропорциональны, т.е. .

Поэтому системы следующего вида решаются аналогично, с разницей только количества свободных переменных:

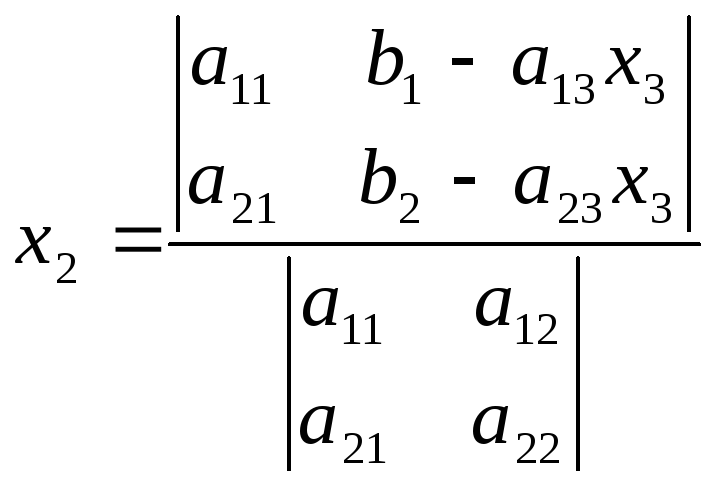, , - произвольное.

Пример:

.

Свойства определителей 2-го порядка

Свойство 1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами (транспонирование).

Доказательство:

.

Свойство 2. При перестановке двух строк (столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину.

Доказательство: Например, пусть

.

Свойство 3. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.

Доказательство: Например, пусть и , тогда

.

Свойство 4. Общий множитель всех элементов строки (или столбца) можно выносить за знак определителя.

Доказательство: Например, пусть

.

Свойство 5. Если к элементам какой-либо строки (столбца) определителя прибавит соответствующие элементы другой строки (столбца), умноженное на одно и то же число, то определитель не изменит своей величины.

Доказательство: Например, пусть

Свойство 6. Если все элементы какой-либо строки (столбца) определителя умножеть на одно и то же число , то и значение определителя умножится на это число .

Свойство 7. Определитель, у которого элементы двух строк (столбцов) соответственно пропорциональны, равен нулю.

Доказательство: Например, пусть и , тогда

.

Свойство 8. Пусть каждый элемент некоторой строки (столбца) определителя есть сумма двух слагаемых. Тогда этот определитель равен сумме двух определителей, причем в одном определителе одноименная строка (столбец) состоит из первых слагаемых, а в другом – из вторых слагаемых. Остальные элементы у определителей одинаковы.

Доказательство: Например, пусть

.

Свойство 9. Если все элементы, кроме главной диагонали, равны нулю, то определитель равен произведению элементов, стоящих на главной диагонали.

2. Определитель матрицы 3х3. Для квадратной матрицы 3-го порядка определитель или детерминант задается следующим образом:

,

называемое разложением определителя по первой строке.

Раскрывая входящие в это выражение определители второго порядка, получаем:

.

Определение. Минором называется определитель матрицы, получившейся из исходной вычеркиванием -й строки и -го столбца.

Следовательно,

Определение. Число называется алгебраическим дополнением элемента . Тогда формула (**) примет более изящный вид: .

Все свойства определителей второго порядка справедливы и для определителей третьего порядка.

Свойство 10. Теорема. Справедливы разложения определителя третьего порядка как по произвольной строке, так и по произвольному столбцу, т.е. определитель третьего порядка равен сумме парных произведений элементов какой-либо его строки (или столбца) на их алгебраические дополнения.

Это следует из перестоновочности строк и столбцов и транспонирования.

Свойство 11. Сумма парных произведений элементов какой-либо его строки (или столбца) на алгебраические дополнения соответствующих элементов какой-либо другой строки (или столбца) равна нулю.

Определение. Определителем -го порядка

называется число, равное алгебраической сумме , где - соответствующие алгебраические дополнения, т.е. являются определителями -го порядка, получаемым из исходного вычеркиванием первого столбца и -й строки и умножением полученного определителя на . Все рассмотренные свойства определителей второго и третьего порядков имеют место и для определителей -го порядка.

2.11. Системы линейных уравнений. Основные понятия. Пусть дана система линейных уравнений:

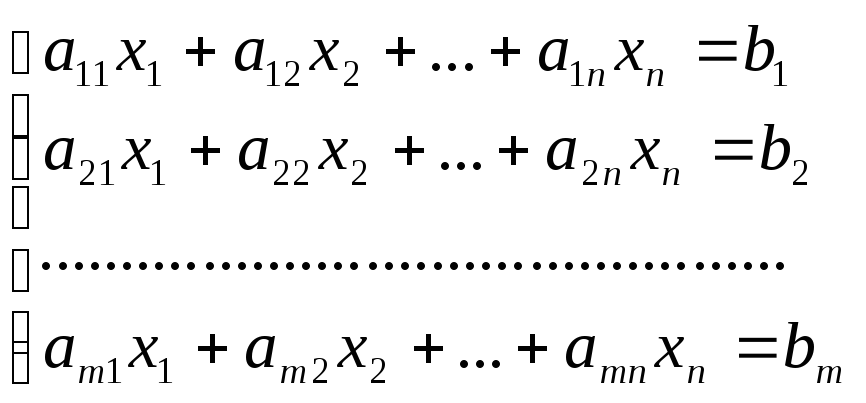
Решением системы линейных уравнений называется набор чисел , при подстановке которых в уравнения вместо соответствующих переменных получаются верные числовые равенства.

Если система имеет хотя бы одно решение, она называется совместной. Если это решение единственное, она называется определенной. Если это решение не единственное, она называется неопределенной.

Если система не имеет решений, она называется несовместной.

Система называется однородной, если все правые части равны нулю: Если хотя бы одно из чисел не равно нулю, система называется неоднородной.

Заметим, что однородная система всегда совместна, т.к. она всегда имеет нулевое решение . Это решение обычно называют тривиальным.