13. Процесс унификации измерительных шкал анализируемого набора частных критериев.

Ответ:

0< x^(j) <N ( 0- самое плохое, N –наилучшее)

1. w₁ =w₂ =…= w_p = 1/p – так как синтетические категории характеризуются 14 показателями, будем считать, что эти показатели равнозначны.

2. Прямая экспертная оценка w₁ ,w_2, …, w_p . Эксперт должен сказать, что в категории «качество жизни» имеет наибольший вес продолжительность жизни и на сколько вес данного показателя больше остальных.

Оценка весов w₁ ,w_2, …, w_p при наличии экспертного «обучения»:

1. Идеальны случай: оценка каждого веса или интегральная оценка. Наиболее информативный и наиболее трудный для экспертов – попросить экспертов оценить свойства интегральных весов по 10 бальной шкале.

Будем иметь y_{1 эксп.} , y _2эксп. , ….y _{n эксп.} при n = 79.

Бальные оценки качества населения i :

Будем строить регрессию y на по оценке МНК.

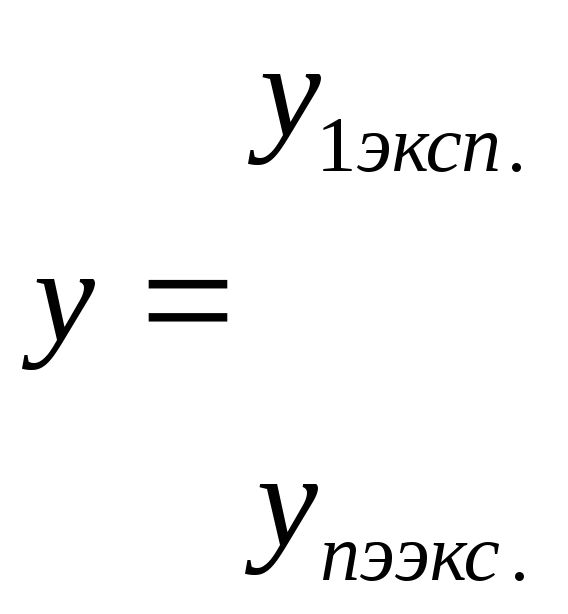
y_{i эксп.} - можно привести к унифицированной шкале.

редкий случай получить оценку от эксперта, чем получить веса по отдельным категориям.

2. Экспертная информация – не просим оценить в баллах, а просим разбить на некоторое количество групп (получаем 3 группы по анализируемым синтетическим категориям объектов).

Самая детальная информация- приписывание ранга каждому объекту (измеряем объект не в шкале, а по рангам). R_i = 2 , т.е. ставим i- объект на второе место.

Y_i : 1) 1- лидеры, i-объект попал в первую группу

2) 2 – середняки, i-объект попал во вторую группу

3. 3 – аутсайдеры, , i-объект попал в третью группу

(число групп = числу объектов)

Оценка параметров модели множественного выбора ( сводится к последовательному приведению анализа к логит- модели).

3. Для каких пар множеств есть парное сравнение. У экспертов просим узнать для каких пар множеств даны характеристики, т.е. парное сравнение. эксперт выбирает пары и по этим парам в бинарной форме дает характеристику – какой из объектов жизни по анализируемым качествам

полная матрица для γ – матрица n*n.

выбрал какие-то элементы, которые известны, остальные нам не известны

Имеем интегральный показатель y, т.е. знаем w_j w_{l = известно}

Можно сформулировать матрицу парных сравнений i,j – y_i – y_j =

Если это >0, то это лучшее качество

Вычислим

Евклидова нормальная матрица А и В (одинаковой размерности).

Подберем веса так, что веса в матрица наименьшим образом расходились.

А = а_i,j , В = b_i,j

Возьмем ту часть матрицы W, которая равна матрице γ

Тогда находим вектор , чтобы парные сравнения, полученные от экспертов, минимально отличались от весов.

Этот метод – экспертно – статистический метод. При наличии двух типов информации: 1) информация, которая статистически записывается; 2)информация от экспертов

14. В Вашем распоряжении результаты обследования стран по 3 показателям, характеризующим уровень их социально-экономического развития:

• по x⁽¹⁾$/чел. в год – ВВП на душу с учетом паритета покупательной способности местной валюты;

• по x⁽²⁾ раз – коэффициенту фондов;

• по x⁽³⁾ тяжких преступлений/100 тыс. населения в год – уровню преступности в стране.

Опишите подробно построения интегрального индикатора социально-экономического развития страна в виде линейной свертки трех унифицированных исходных показателей (под унифицированностью понимается такое его преобразование к десятибалльной шкале измерения, при котором значения 10 и 0 определяют, соответственно, наихудшее и наилучшее качество по рассматриваемому показателю).

Ответ:

Имеется x⁽¹⁾,x⁽²⁾,x⁽³⁾ – надо -> y=f(x⁽¹⁾,x⁽²⁾,x⁽³⁾), где y-скалярный интегральный показатель качества жизни. Его мультикритериальная схема выглядит следующим образом:

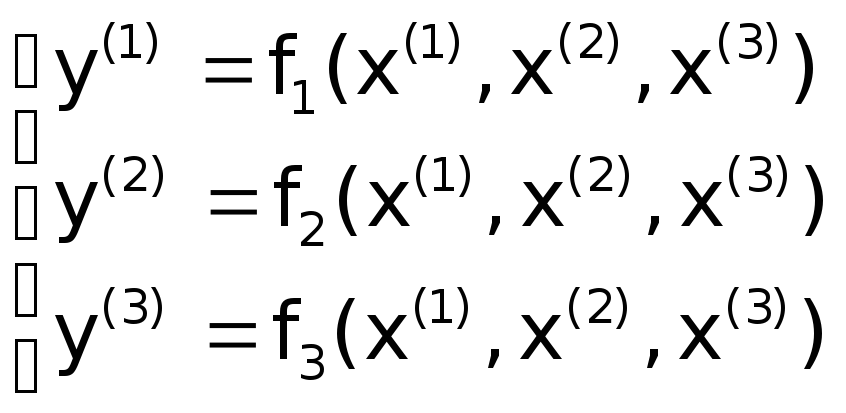
w_j (веса) необходимо определить.

Существует две возможности подсчета: исходя из того, что каждый показатель значим одинаково (1/3) и исходя из экспертных оценок. Т.к. имеется возможность бальной оценки, то будем использовать второй способ. Этот способ наиболее информативный, но и наиболее трудный.

Этапы:

1. Эксперты по 10 бальной шкале оценивают показатели социально-экономического развития. Имеем y_{1 эксп}, y_{2 эксп}… y_{N эксп} , где N – число обследуемых стран.

2. Можем определить веса, т.к. для каждого i имеем x⁽¹⁾_i x⁽²⁾_i x⁽³⁾_i для i от 1 до n

3. Можем построить регрессию y от x⁽¹⁾,x⁽²⁾,x⁽³⁾ МНК.

y_{i эксп} = β₀+β₁x⁽¹⁾_i+β₂x⁽²⁾_i+β₃x⁽³⁾_i+ε_i

Введя обозначения, имеем:

=>

y_{i эксп} можно привести к log шкале -> ввести Тогда 0<y<N.

Но вообще говоря – это довольно редкий случай, т.к. интегральную оценку получить легче, чем оценку весов.

15. Известна функция плотности f(x) распределения всего населения региона по величине среднедушевого дохода ξ (тыс. руб.). Требуется вывести (в терминах f(x)) функцию плотности распределения только бедного населения, т.е. населения, среднедушевые доходы которого не превышают x₀=2.5 тыс.руб.

Ответ:

Для бедного населения

Теперь по функции распределения перейдем к функции плотности

, где

16. Известна функция плотности f(x) распределения всего населения России по величине среднедушевого дохода. Требуется вывести в терминах f(x) функцию плотности распределения только богатого населения.

Ответ:

17. Распределение богатого населения по величине среднедушевых доходов описывается законом Парето.

Ответ:

Дано:

Доля населения с доходами > 20 тыс.руб. равна 8%.

Решение:

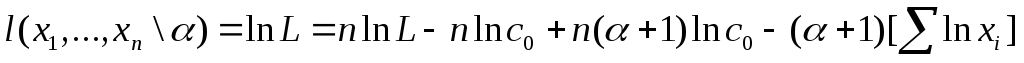
где g=32

=20

18. Что такое функция Лоренца?

Ответ:

Функция Лоренца – оценка степени концентрации доходов.

L(q) – доля доходов, которые распределены доля для беднейшего населения.

0A – полная уравниловка.

0CA – кривая Лоренца.

k – полная дифференциация, сосредоточение средств в одних руках

Функция плотности:

19. Что такое коэффициент фондов? Выведите его выражение в терминах функции плотности f(x) распределения населения анализируемой территории по среднедушевым доходам.

Вычислите значения коэффициента фондов:

1) в условиях полной уравниловки (все население с одинаковым среднедушевым доходом);

2) в условиях экстремальной дифференциации (весь доход территории сосредоточен в одних руках);

3) при равномерном (на отрезке [0;100000руб.] и на отрезке [0;10000руб.]) распределении населения по величине среднедушевого дохода.

Ответ:

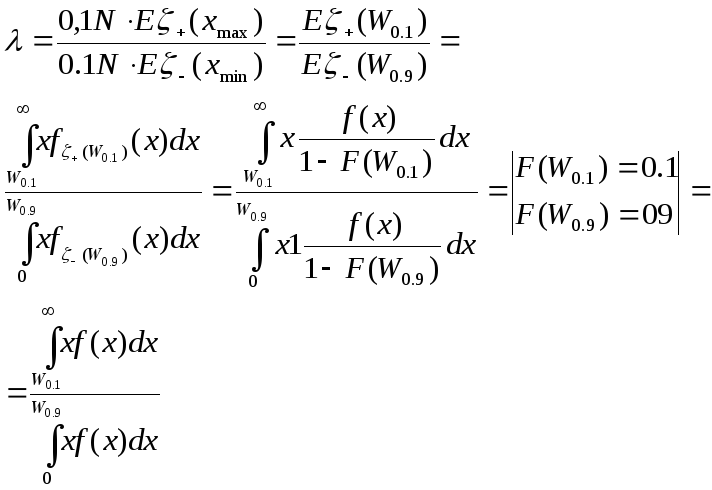
При равномерном:

для социально благополучных стран должен быть равен 8.

20. Пусть - черта бедности, N- общая численность населения региона и f(x) – функция плотности распределения населения этого региона по величине среднедушевого дохода. Вывести сумму S адресной помощи бедным, необходимую для полного устранения бедности в регионе.

Ответ:

- для помощи бедным.

Доля бедных -

Глубина бедности -

S – сумма, необходимая для полного устранения бедности. Каждому i-ому бедному с доходами должны выплатить сумму (доход станет =b)

N – общая численность.

q(b) – доля бедных.

- сумма, которую получит бедный с доходом x из общей суммы

Способ распределения социальной помощи:

- плотность распределения.

Глубина бедности -

Решение:

относ. b’