45. Можно ли определить момент инерции маятника Оберберка в лабораторной работе №4 «Изучение основного закона динамики вращательного движения» ,используя закон сохранения механической энергии?

Если Т - сила натяжения нити, .

Силу натяжения нити можно найти из уравнения движения груза:

,

тогда

Момент сил трения М_тр обычно оказывается доволь­но велик и зависит от скорости вращения, М_тр способен существенно исказить результаты опыта, однако, в первом приближении можно принять момент сопротивления постоянным и не зависящим от скорости, тогда с учетом момента силы трения уравнение можно записать в виде: М-M_тр ()

46. Дайте определение физического маятника. Физическим маятником называется твердое тело произвольной формы, укрепленное на неподвижной горизонтальной оси( не проходящей через его центр масс) и способное совершать колебания относительно этой оси.

Период колебаний физического маятника выражается по следующей формуле:

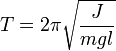
где J — момент инерции маятника относительно оси вращения, m — масса маятника, l — расстояние от оси вращения до центра масс.

47.Дайте определение математического маятника. Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен

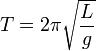
и не зависит от амплитуды и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы. При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.Математический маятник – это абстрактное представление о грузе, имеющем массу, но не имеющем объема, подвешенном на невесомой нерастяжимой нити, длина которой многократно превосходит амплитуду колебаний. Реальным приближением к этому является тяжелый шарик, подвешенный на длинной тонкой нити, совершающий колебания небольшой амплитуды. Математический маятник подчиняется законам движения, по которым можно определить период его колебаний, зная длину нити и ускорение свободного падения в данном месте. Место может быть любое – хоть Луна или Марс, главное – знать ускорение свободного падения. Интересно, что период колебаний математического маятника не зависит от его массы.

Формулы для решения: .

48. Какие колебания называются гармоническими? По какому закону изменяется смещение при гармоническом колебании ?

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса. Уравнение гармонических колебаний имеет вид:

, где A - амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия); - круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса - называется фазой колебаний. Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания. Значение начальной фазы определяется выбором начала отсчета. Величина x может принимать значения, лежащие в пределах от -A до +A. Промежуток времени T, через который повторяются определенные состояния колебательной системы, называется периодом колебаний. Косинус - периодическая функция с периодом 2π, поэтому за промежуток времени T, через который фаза колебаний получит приращение равное 2π, состояние системы, совершающей гармонические колебания, будет повторяться. Этот промежуток времени T называется периодом гармонических колебаний. Период гармонических колебаний равен: T = 2π/. Число колебаний в единицу времени называется частотой колебаний ν. Частота гармонических колебаний равна: ν = 1/T. Единица измерения частоты герц (Гц) - одно колебание в секунду. Круговая частота = 2π/T = 2πν дает число колебаний за 2π секунд. Гармонические колебания лежат в основе единого подхода при изучении колебаний различной природы, так как колебания, встречающиеся в природе и технике, часто близки к гармоническим, а периодические процессы иной формы можно представить как наложение гармонических колебаний. Простейшим видом колебаний являются гармонические колебания — колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса. Так, при равномерном вращении шарика по окружности его проекция (тень в параллельных лучах света) совершает на вертикальном экране (рис. 13.2) гармо-ническое колебательное движение. Смещение от положения равновесия при гармонических колебаниях описывается уравнением (его называют кинематическим законом гармонического движения) вида: или где х — смешение — величина, характеризующая положение колеблющейся точки в момент времени t относительно положения равновесия и измеряемая расстоянием от положение равновесия до положения точки в заданный момент времени; А — амплитуда колебаний — максимальное смещение тела из положения равновесия; Т — период колебаний — время совершения одного полного колебания; т.е. наименьший промежуток времени, по истечении которого повторяются значения физических величин, характеризующих колебание; — начальная фаза; — фаза колебании в момент времени t. Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы (смещение, скорость, ускорение) тела в любой момент времени. Если в начальный момент времени t₀= 0 колеблющаяся точка максимально смещена от положения равновесия, то , а смещение точки от положения равновесия изменяется по закону

Если колеблющаяся точка при t₀ = 0 находится в положении устойчивого равновесия, то смещение точки от положения равновесия изменяется по закону

Величину V, обратную периоду и равную числу полных колебаний, совершаемых за 1 с, называют частотой колебаний:

(в СИ единицей частоты является герц, 1Гц = 1с^-1).Если за время t тело совершает N полных колебаний то

Величину,

показывающую, сколько колебаний совершает тело за 2 с, называют циклической (круговой) частотой.

Кинематический закон гармонического движения можно записать в виде:

Графически зависимость смещения колеблющейся точки от времени изображается косинусоидой (или синусоидой).