41. Как определить направление момента силы?

Для описания динамики вращательного движения твердого тела необходимо ввести понятие момента силы. Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы. Момент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M. При этом надо различать понятия момента силы относительно точки и относительно оси. Если сила f приложена к материальной точке А, то моментом силы М относительно произвольной точки О называется векторное произведение радиуса-вектора r, проведенного из точки О к точке А, и вектора силы:  М = [ r f ] .  Модуль векторного произведения  = r f sin a, а  направление вектора М определяется правилом правого буравчика: направление первого вектора r по кратчайшему пути вращается к направлению второго вектора f, а движение оси буравчика при этом вращении показывает направление вектора М. Моментом силы относительно произвольной оси z называется векторное произведение радиуса-вектора r и составляющей f  силы f , приложенной в точке А:  М = [ r  f  ] где составляющая f   представляет собой проекцию силы f на плоскость, перпендикулярную оси z  и проходящую через точку А , а r - радиус- вектор точки А, лежащий в этой плоскости. M=Fd, т. е. момент силы равен произведению силы F на длину перпендикуляра d, опущенного из оси на направление силы. Длину перпендикуляра, опущенного из оси на направление силы, называют плечом силы. Значит, момент силы равен произведению величины силы на плечо силы. Ясно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента (рис. 120). Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси. Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. Как мы видели, для равновесия необходимо, чтобы силы стремились вращать тело в противоположных направлениях и чтобы произведения сил на их расстояния до оси были равны. Значит, при равновесии моменты обеих сил должны быть равны по величине и противоположны по знаку. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю. Так как момент силы определяется произведением величины силы на плечо, то единицу момента мы получим, взяв силу, равную единице, плечо которой также равно единице. Значит, в системе СИ единицей момента силы является момент силы в 1 н, действующей на плече в 1 м, т. е. 1 н*м, в системе СГС —1 дин*см, в системе МКСС— 1 кГ*м. Пользуясь данными § 45, найдем соотношения между этими единицами:1 дин*см = 10^-7 н*м;   1 кГ*м = 9,8 н*м.

42. Как определить направление угловой скорости?

Углова́я ско́рость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:

,

а направлен по оси вращения согласно правилу буравчика, то есть, в ту сторону, в которую ввинчивался бы буравчик с правой резьбой, если бы вращался в ту же сторону. Единица измерения угловой скорости, принятая в системах СИ и СГС) — радианы в секунду. (Примечание: радиан, как и любые единицы измерения угла, — физически безразмерен, поэтому физическая размерность угловой скорости — просто [1/секунда]).Определим угловую скорость как вектор, величина которого численно равна угловой скорости, b направленный вдоль оси вращения, причем, если смотреть с конца этого вектора, то вращение направлено против часовой стрелки. Исторически сложилось, что положительным направлением вращения считается вращение «против часовой стрелки», хотя, конечно, выбор этого направления абсолютно условен. Для определения направления вектора угловой скорости можно также воспользоваться «правилом буравчика» (которое также называется «правилом правого винта») - если направление движения ручки буравчика (или штопора) совместить с направлением вращения, то направление движения всего буравчика совпадет с направлением вектора угловой скорости.

43. Как определить направление углового ускарения? Угловое ускорение - векторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.Угловое ускорение равно первой производной от угловой скорости по времени.Формула угловой скорости:

Единица углового ускорения - радиан в секунду в квадрате.

Углово́е ускоре́ние — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно^[1]:

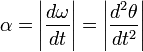
Вектор углового ускорения α направлен вдоль оси вращения (в сторону при ускоренном вращении и противоположно  — при замедленном).

При вращении вокруг неподвижной точки вектор углового ускорения определяется как первая производная от вектора угловой скорости ω по времени^[2], то есть

,

и направлен по касательной к годографу вектора в соответствующей его точке.

44. При каком условии мы имеем право считать в лабораторной работе №4 «Изучение основного закона динамики вращательного движения» линейное ускорение точек на ободе щкива равным ускорению поступательного движения груза?

Момент сил создается грузом m, привязанным к нити Н, ко­торая навита на один из шкивов. Если момент сил трения M_тр, при­ложенный к оси маятника, мал по сравнению с моментом силы натяжения нити, то проверка уравнения не представляет труда. Действи­тельно, измеряя время t, в течение которого груз из состояния покоя опустится на расстояние h, можно легко найти ускорение груза а, в проекции на координатную ось, совпадающую с направлением движения:

, которое связано с угловым ускорением  (при отсутствии проскальзывания нити относительно обода шкива) очевидным соотношением

, где r - радиус шкива.