34.Что понимают под моментом инерции тела относительно некоторой оси? Какой физический смысл имеет момент инерции?

При вращении материальной точки массы т_i по окруж­ности радиуса г_i момент ее импульса в проекции на ось враще­ния равенL_i=m_i_ir_i Линейная скорость движения _i связана с угловой скоростью  соотношением _i=r_i , поэтому L_i=m_ir_i² . Если вокруг оси 0 вращается система материаль­ных точек с одной и той же угловой скоростью , то, где суммирование производится по всем материальным точка системы. Величину , как одинаковую для всех матери­альных точек, можно вынести из под знака суммы, тогда получится

основной закон динамики вращательного движения в проекции на ось вращения можно записать:

,

где М - проекция суммарного момента внешних сил на ось вращения.

Уравнение вращения т.т. вокруг не­подвижной оси:

или

.

Произведение момента инерции твердого тела относительно неподвижной оси вращения на угловое ускорение  равно моменту внешних сил относительно той же оси

35. От чего зависит момент инерции тела? От чего он не зависит? Момент инерции тела- физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела,а также от выбора оси вращения, характеризует инертность тела при вращательном движении.

36.Как найти момент инерции материальной точки?

Пользуясь уравнением M=I dω/dt=Iβ и определив момент действующих сил и угловое ускорение, можно вычислить момент инерции тела. Часто в экспериментальных работах тело приводится во вращение или колебание с помощью груза, падающего с некоторой высоты. Потенциальная энергия падающего груза переходит в кинетическую энергию вращательного движения тела. Используя закон сохранения механической энергии при условии малых потерь на трение, можно вычислить момент инерции тела.

37.Как найти момент инерции тела, которое в данных условиях нельзя считать материальной точкой?

38. Какая формула упрощает расчёт момента инерции тела относительно оси, не проходящей через центр масс?

т.Гюйгенса - Штейнера, момент инерции груза относительно оси вращения:

, где R - расстояние между осью вращения и осью, проходящей через центр масс полого цилиндра параллельной оси вращения.

Момент инерции от-но произвольной оси = сумме от-но, оси параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между ними

39. В методе колебаний для определения момента инерции диска в лабораторной работе №3 «Определение момента инерции диска» применяется теория малых колебаний .Какие упрощения при этом допускаются?

Момент инерции тела – физическая величина, аналогичная массе при поступательном движении; она зависит от формы, размеров, массы тела и ее распределения внутри тела, а также от выбора оси вращения, и характеризует инертность тела при вращательном движении.

Определение момента инерции диска методом колебаний

В работе используется установка, на ободе которой укреплен массивный шар

Рис.3.2. Схема экспериментальной установки для определения момента инерции диска методом колебаний.

Пренебрегая моментом сил трения, можно написать уравнение движения диска с шаром в следующем виде:

, (3.5) (3.5)

где I- момент инерции диска c валом относительно оси вращения OO, I₁ - момент инерции шара относительно оси вращения OO, вычисляемый по теореме Гюйгенса – Штейнера:

, (3.6)

где R и R₁ – радиусы диска и шара соответственно, m₁ - масса шара,  – угол отклонения диска от положения равновесия.

При малых углах отклонения можно принять sin ≈  и уравнение (3.5) можно написать в виде:

. (3.7) (3.7)

Как известно, решением такого дифференциального уравнения будет периодическая функция

, (3.8) (3.8)

где α₀- угловая амплитуда колебаний,  - начальная фаза, ω₀ - циклическая частота колебаний:

. (3.9) (3.9)

Измерив период колебаний диска с шаром Т₀ и зная массу m₁ и радиус шара R₁, из формул (3.6) и (3.9) найдем момент инерции диска относительно оси вращения:

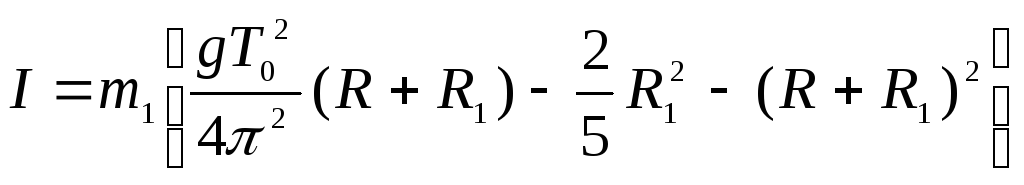. (3.10)

40.Перечислите причины, дающие погрешность в лабораторной работе №3 «Определение момента инерции диска» Скажется ли на точности измерений колебание груза при его падении, а также неуровновешенность диска?