1. Дайте определение абсолютной и относительной погрешности.

Абсолютной погрешностью приближенного значения называется модуль разности точного и приближенного значений.Относительной погрешностью приближенного значения называется отношение абсолютной погрешности к модулю приближенного значения. Е=дельта х/<x>

2)Как классифицируются погрешности по свойствам .

Систематические и случайные,грубые

Факторы,постоянные или закономерно изменяющиеся в процессе измерительного эксперимента,например,начальное отклонение стрелки прибора от нуля, являются систематическими погрешностями.Систем.погрешности делятся на приборные,методические и метода обработки данных. Методические погрешности происходят от несовершенства метода измерения, использования упрощающих предположений и допущений при выводе применяемых формул, влияния измерительного прибора на объект измерения. Например, измерение температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима объекта измерения вследствие внесения термопары. Приборные- зависят от погрешностей применяемых средств измерения. Неточность градуировки, конструктивные несовершенства, изменения характеристик прибора в процессе эксплуатации и т. д. являются причинами основных погрешностей инструмента измерения. Дополнительные погрешности, связанные с отклонением условий, в которых работает прибор, от нормальных, отличают от инструментальных т. к. они связаны скорее с внешними условиями, чем с самим прибором. Метод обработки данных-вызываются неправильными отсчетами показаний прибора человеком (оператором). Например, погрешность от параллакса, вызванная неправильным направлением взгляда при наблюдении за показаниями стрелочного прибора. Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности. Случайные погрешности-это составляющая погрешности измерения,изменяющиаяся случайным образом при повторных измерениях одной и той же величины. К ним можно отнести наряду со случайными изменениями напряжения в электросети,температуры в лаборатории и др.факторы,связанные с несовершенностью органов чувств человека и его навыковых качеств. Чтобы уменьшить случайную погрешность нужно:1)уменьшить влияние внешних факторов.2)Проводить измерения внимательно и тщательно 3)увеличить число опытов.

3,Какими свойствами обладает нормальное распределение случайных погрешностей?

Методы обработки результатов прямых измерений, содержащих случайные погрешности. Пусть в одних и тех же условиях проделано N измерений и х_i – результат i-го измерения. Наиболее вероятное значение измеряемый величины – ее среднеарифметическое значение . (1.2)

Величина <х> стремится к истинному значению х₀ измеряемой величины при N. Средней квадратичной погрешностью отдельного результата измерения называется величина

.

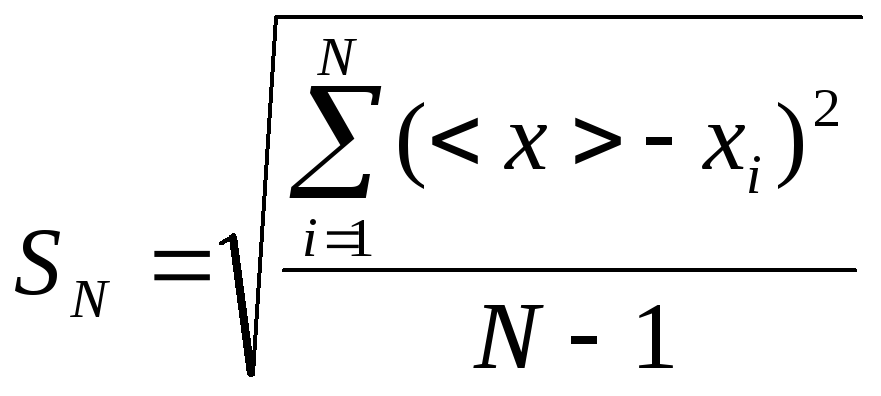При N S_N стремится к постоянному пределу :

. (1.4)

Величина ² называется дисперсией результатов измерений.

. ). При большом числе измерений отношение n_i /N характеризует вероятность появления значений измеряемой величины в данном интервале с шагом L. Если n_i /N разделить на величину шага интервала L, то значение величины будет характеризовать относительное число благоприятных случаев в единичном интервале. Диаграмма, построенная для y_i, показывает распределение плотности вероятности по интервалам и называется приведенной гистограммой

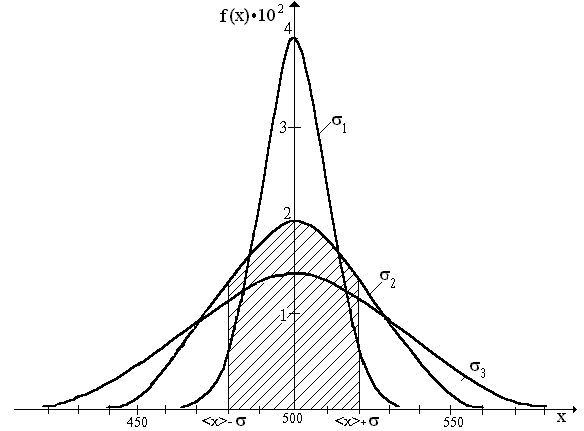
. Кривые распределения Гаусса для различных значений  ₁=10, ₂=20 и ₃=30. .

На рис. 1.3. изображены кривые распределения, соответствующие различным  . Из этого рисунка видно, что при малом  кривая уже, а максимум выше, что соответствует более доброкачественным измерениям.

Распределение, соответствующее предель-ной кривой, называют нормальным (гауссовым) распределением. Оно описывается функцией распределени , (1.5)

где ²– как уже сказано выше, является дисперсией,  - характеризует разброс измерений относительно среднеарифметического значения и называется стандартным отклонением или среднеквадратичной погрешностью.

Функция Гаусса является нормированной, т.е. f(x) удовлетворяет соотношению:

. (1.6)

Интеграл имеет бесконечные пределы. Это означает, что измеряемая величина с вероятностью 1 (или 100%) лежит в пределах от - до + , или то, что нахождение измеряемой величины в этих пределах является событием достоверным. Функция плотности вероятности обладает следующими свойствами (см. рис. 1.2.):

- симметрична относительно х,

-достигает максимального значения в точке х,

- быстро стремится к нулю, когда |х_i-х| становится большим по сравнению с  .