5.8. В чем состоит задача коммивояжера?
Пусть
имеется
пунктов,
занумерованных в некотором порядке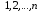
.
Для каждой пары
этих
пунктов известно “расстояние”
.
Термин “расстояние” может означать
физическое расстояние между этими
пунктами, время перехода из пункта
в пункт
,
стоимость такого перехода или количество
затраченного горючего. Значения
образуют квадратную матрицу
,
у которой элементы на главной диагонали
не определены и, например, обозначены
символом
.
В этой матрице не обязательно
,
то есть она может быть не симметричной.
Коммивояжер, начиная от некоторого начального пункта, например, пункта 1, должен обойти все остальные, побывав в каждом пункте по одному разу таким образом, чтобы его маршрут был оптимален по какому-либо критерию. Чаще всего оценкой маршрута является его “длина” как сумма “расстояний” непосредственных переходов в выбранном маршруте. Коммивояжер должен выбрать маршрут наименьшей длины.
5.9. Построить математическую модель задачи коммивояжера.
Через
обозначим переменные, такие, что
,
если коммивояжер включил в свой маршрут
переход от пункта
до пункта
,
и
,
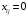в противном случае. В задаче необходимо
определить значения
,
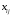при которых функция
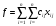(5.2.1)
принимает минимальное значение и для которых выполняются условия
,
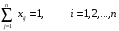(5.2.2)
,
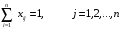(5.2.3)
,
(5.2.4)
множество
должно
определять замкнутый маршрут.
(5.2.5)
Условие
(5.2.2) говорит о том, что коммивояжер
обязан переходить из пункта
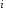только в один из остальных пунктов.
Условие (5.2.3) требует, чтобы в каждый
пункт
осуществлялся переход только из одного
пункта.
Целевая функция (5.2.1) и ограничения (5.2.2)-(5.2.4) в точности совпадают с моделью классической задачи о назначениях (§3.6). Проанализируем детально сущность дополнительного условия (5.2.5).
Условие (5.2.5) требует, чтобы любой маршрут коммивояжера был полным циклом.
5.10. В чем разница между моделями классической задачи о назначениях и задачей коммивояжера?
Разница
заключается в условии (5.2.5). Это означает,
что если на матрице расстояний
в задаче коммивояжера решить задачу о
назначениях с минимизацией целевой
функции и если это решение будет полным
циклом, то оно одновременно будет
решением задачи коммивояжера.
5.11. Сформулировать одностадийную задачу без задержек в обслуживании заявок.
Пусть
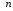заявок необходимо обслужить на одном
приборе, причем известны времена
,
продолжительностей такого обслуживания.
Кроме того, известно, что если после
обслуживания заявки
будет обслуживаться заявка
,
то необходима переналадка прибора,
которая длится
единиц времени. Эти величины образуют
матрицу
.
Задача состоит в том, чтобы найти такую очередность обслуживания всех заявок, при которой суммарное время обслуживания будет минимальным.
Если
перестановка
определяет очередность обслуживания
заявок, то общее время этого обслуживания
равно
.
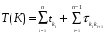Очевидно,
что первое слагаемое в этой сумме не
зависит от порядка обслуживания и
является величиной постоянной. Второе
слагаемое зависит от очередности
обслуживания и поиск оптимальной
очередности сводится к поиску перестановки,
которая минимизирует
.
Если все
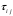представить на расширенной матрице
то, очевидно, что решение задачи коммивояжера для этой матрицы “расстояний ” определит искомое оптимальное расписание для нашей одностадийной задачи обслуживания заявок. Оно получится из оптимального маршрута коммивояжера с началом в пункте 0 формальным удалением этого пункта.