
- •35. Постановка задач оптимального управления. Фазовые и управляющие переменные. Амплитудные ограничения. Примеры
- •37. Критерии качества управления. Типы критериев качества
- •38. Классификация задач оптимального управления по типу ограничений фазовые переменные.
- •39. Распространенные задачи оптимального управления. Основные проблемы теории управляемых процессов.
- •40. Принцип максимума л.С. Понтрягина в теории оптимальных систем
- •41. Метод динамического программирования р. Беллмана
- •42. Применение принципа максимума, как проверочного условия
- •43.Применение принципа максимума для сведения задачи оптимального управления к решению двухточечной краевой задачи.
- •45. Принцип максимума л.С. Понтрягина для задач Больца, Лагранжа
- •46. Принцип максимума л.С. Понтрягина для задач терминального управления
- •48. Свойства функции Гамильтона. Достаточность принципа максимума для линейных систем
- •47.Задачи синтеза оптимального управления по быстродействию
- •24. Процесс управления и требования к нему. Итд
42. Применение принципа максимума, как проверочного условия
Пример
1. Пусть
система имеет вид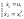
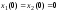 ,
,
 .
.
Ограничения
на управление имеют вид
 (модульные ограничения на
управление).J(u)=(x(1))=
–x2(1)
(модульные ограничения на
управление).J(u)=(x(1))=
–x2(1)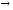 min.
min.
Допустим, задано управление u(t) ≡ 1. Исследуем это управление на оптимальность с помощью принципа максимума.
H(x,
ψ,
u,
t)
= ψ1u+ψ2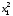 .
.
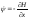 .
.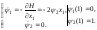
Отсюда
следует, что ψ2(t)≡1.
H(x,
ψ,
u,
t)
= ψ1u+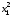 .
.
Найдем фазовую траекторию, которая соответствует выбранному управлению. При управлении u=1 получим
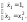
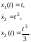
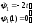 ψ1(t)=1–
t2.
ψ1(t)=1–
t2.
H(t,
u)=(1–
t2)u
+ t2,
0 t
t 1,
1,
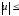 2.
2.
H(t,u) достигает своего максимального значения на управлении u(t)≡2.
Рис. 12.1. Применение принципа максимума Л.С.Понтрягина как проверочного условия
Исходное
управление u(t)≡1
не удовлетворяет принципу максимума..
Если ограничения имеют вид
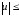 1,
то исходное управление удовлетворяет
необходимым условиям оптимальности
1,
то исходное управление удовлетворяет
необходимым условиям оптимальности
43.Применение принципа максимума для сведения задачи оптимального управления к решению двухточечной краевой задачи.
Управление
исключим из рассмотрения с помощью
условия принципа максимума функции Н.
Обозначим
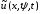 управление, которое доставляет максимум
функции H при произвольных х, ψ, t, т.е.
управление, которое доставляет максимум
функции H при произвольных х, ψ, t, т.е.
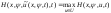 .
.
Рассмотрим
случай амплитудных ограничений. Допустим,
что эта задача решена. Подставим
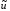 в исходную и сопряженную системы.
Получаем замкнутую систему 2n
дифференциальных уравнений:
в исходную и сопряженную системы.
Получаем замкнутую систему 2n
дифференциальных уравнений:
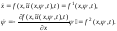 (12.4.1)
(12.4.1)
Краевые
условия:
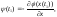
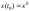 .
(12.4.2)
.
(12.4.2)
Получаем
замкнутую систему 2n
дифференциальных уравнений с 2n
краевыми условиями. Полученная задача
(12.4.1), (12.4.2) является конечномерной
задачей поиска начальных значений для
сопряженной системы ψ(t0).
Нужно найти такой вектор
 (t0),
чтобы выполнялось первое из условий
(12.4.2).
(t0),
чтобы выполнялось первое из условий
(12.4.2).
Пусть
x*(t),
ψ*(t)
решение краевой задачи (12.4.1), (12.4.2). Тогда
управление u*(t)=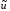 (x*(t),
ψ*(t),
t)
(x*(t),
ψ*(t),
t)
Рис. 12.2. Применение принципа максимума Л.С. Понтрягина для выявления структуры оптимального управления
удовлетворяет принципу максимума и в общем случае подозрительно на оптимальность. Если удастся показать, что решение краевой задачи (12.4.1), (12.4.2) единственно, то уп-равление u*(t) и будет оптимальным управлением.
45. Принцип максимума л.С. Понтрягина для задач Больца, Лагранжа
Рассмотрим
задачу Больца
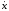 =
f(x,
u,
t),
x(t0)=x0,
=
f(x,
u,
t),
x(t0)=x0,
u(t) U,
t0
≤ t
≤ t1.
(13.1.1)
U,
t0
≤ t
≤ t1.
(13.1.1)
J(u)=g(x(t1))
+
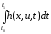
Запишем
необходимые условия оптимальности для
задачи (13.1.1), используя результат,
полученный для задачи терминального
управления. Приведем задачу (13.1.1) к
задаче терминального управления с
помощью введения новой фазовой переменной
xn+1(t)
=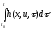 .
.
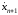 =
h(x,
u,
t),
xn+1(t0)
= 0.
=
h(x,
u,
t),
xn+1(t0)
= 0.
Получаем задачу терминального управления, но размерности (n+1)
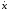 =
f(x,
u, t),
x(t0)
= x0,
=
f(x,
u, t),
x(t0)
= x0,
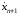 =
h(x,
u, t),
xn+1(t0)
= 0, u(t)
=
h(x,
u, t),
xn+1(t0)
= 0, u(t) U.
J(u)
= g(x(t1))
+ xn+1(t1).
U.
J(u)
= g(x(t1))
+ xn+1(t1).
Запишем необходимые условия оптимальности для полученной задачи терминального управления:
H = H(x, ψ, ψn+1, u, t) = ψ´f(x, u, t) + ψn+1h(x, u, t).
Определим
уравнение для ψn+1
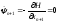 .
ψn+1(t1)
= -1.
.
ψn+1(t1)
= -1.
Отсюда следует, что ψn+1(t) ≡ -1.
Тогда H(x, ψ, u, t) = ψ´f(x, u, t) – h(x, u, t) (13.1.2)
Сопряженная
система для вектор-функции ψ имеет вид
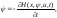
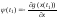 .
.
В общем случае это линейная неоднородная система. Для оптимальности управления необходимо, чтобы оно удовлетворяло принципу максимума.
Следовательно, для формулировки необходимых условий оптимальности для задачи Больца (13.7.1) надо составить функцию Гамильтона Н вида (13.1.2). Для оптимальности допустимого управления u(t) необходимо, чтобы функция Гамильтона Н достигала максимума по всем допустимым управлениям.
Аналогично формулируется принцип максимума для задачи Лагранжа. Только в этом случае
ψ(t1) = 0, (т.к. g(x(t1)) = 0).
Теорема
13.. Для линейной
задачи Больца
 =A(t)x
+ b(x,
u),
x(t0)
= x0,
u(t)
=A(t)x
+ b(x,
u),
x(t0)
= x0,
u(t) U,
t0
≤ t
≤ t1.
J(u)
= g(x(t1))
+
U,
t0
≤ t
≤ t1.
J(u)
= g(x(t1))
+
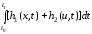 ,где
g(x)
и h1(x,
t)
выпуклые по х функции, принцип максимума
есть необходимое и достаточное условие
оптимальности.
,где
g(x)
и h1(x,
t)
выпуклые по х функции, принцип максимума
есть необходимое и достаточное условие
оптимальности.
