35. Постановка задач оптимального управления. Фазовые и управляющие переменные. Амплитудные ограничения. Примеры
динамические объекты – это такие объекты, характеристики которых меняются с течением времени t
.
Состояние
объекта в любой момент времени t
характеризуется n действительными
числами
которые называются координатами объекта.
Движение будет заключаться в том, что
эти переменные будут меняться с течением
времени, т.е. являются функциями времени
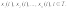
Удобно ввести в рассмотрение вектор
Этот вектор называется фазовым вектором.
Введем
пространство X, соответствующее этим
фазовым состояниям, которое назовем
фазовым пространством объекта
.
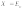Любое состояние управляемого объекта
характеризуется точкой фазового
пространства, а движение управляемого
объекта x(t) есть некоторая кривая в
фазовом пространстве.
При n=2 получим фазовую плоскость.
Мы предполагаем рассматриваемый объект управляемым, т.е. имеем возможность изменять входные величины системы, изменения которых влияет на состояние системы. Это значит, что в любой момент времени можно выбирать r управляющих воздействий
которые воздействуют на состояние объекта.
Управление
для любых
состоит
в том, что выбираются функции (управляющие
воздействия) в некоторый промежуток
времени
Удобно ввести вектор-функцию
,
u– управляющее воздействие.
Это управление можно выбирать произвольным образом при сделанных ограничениях. Фазовая же траектория х(t) зависит от выбираемого управления.
Выбор
управления
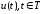однозначно определяет фазовое поведение
изучаемого объекта. Таким образом,
управление – независимый параметр.
Схематически управляемый объект может быть изображен следующим образом
На вход управляемого объекта подается управляющее воздействие
Рис. 9.1. Схема управления движением объекта.
В результате получаем фазовое поведение управляемого объекта управления.
Пример. Рассмотрим движение ракеты. Ракету можно рассматривать как точку переменной массы. Три величины определяют положение ракеты в пространстве.
–
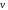скорость
(три переменные),
–
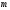масса,
(масса также изменяется).
В результате получаем семь фазовых переменных, т.е. n=7.
Амплитудные ограничения
Амплитудные ограничения связаны с ограничениями на амплитуду управляющей
функции в любой момент времени t.
Зададим
в пространстве переменных
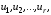некоторое ограниченное множество
U.
Это множество r-мерного евклидового
пространства:
.
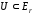Ограничение на управление состоит в том, что в любой момент времени t управление
выбираем
так, чтобы
.
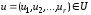Таким
образом, для любого
:
.
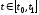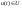(9.3.1)
Область
U задается при математическом описании
управляемого объекта. (Область управления
U – это область допустимых управлений).
Рис. 9.3. Возможный вид области допустимых управлений
для случая r=2.
и
нужно
выбирать так, чтобы в любой момент t
.
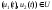Если граница принадлежит множеству U, то управление u(t) может находиться и на границе. Для многих случаев важен случай замкнутой области U.
Рассмотрим частные, наиболее важные случаи амплитудных ограничений.
а) Параллелепипедные ограничения
,
.
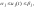
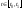Такие ограничения называются параллелепипедными ограничениями, поскольку об-
ласть
U представляет собой многомерный
параллелепипед. Если r=1, то получим
отрезок:
.
Если r=2,
то получим прямоугольник
,
.
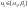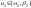Рис.
9.4. Пареллелепипедные ограничения на
управление
(случай r=2).
Параллелепипедные ограничения являются наиболее распространенными.
б) Модульные ограничения на управление
При модульных ограничениях любая компонента ограничена по модулю. Модульные
ограничения являются частным случаем первого типа ограничений.
,
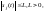
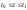
Область
управления есть r-мерный
куб с центром в начале координат, т.е.
нулевое управление удовлетворяет
ограничению. Любое управление
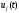ограничено независимо от остальных.
с) Ограничения типа сферы
Областью управления является r-мерная сфера с центром в начале координат.
В общем случае амплитудные ограничения могут быть описаны в виде неравенств
,
-
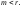
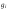произвольные заданные функции.