5 Преобразование чертежа

Решение многих задач значительно упрощается, если геометрические объекты занимают частное положение по отношению к плоскостям проекции. Существуют специальные способы преобразования чертежа к такому виду, примером может служить перемена плоскостей проекций (любое преобразование чертежа можно свести к конечному числу переносов и поворотов плоскости).

Преобразуем прямую общего положения t в прямую уровня (рисунок 15).

1) Заменим плоскость π₂ на новую плоскость π'₂ . Для этого проведем ось чертежа Х₁ параллельно проекции t₂.

2) Сохраняя значение координаты z , строим проекцию t'₁. В новой системе координат прямая t стала линией уровня.

Рисунок 15

Рисунок 16

Введение еще одной плоскости проекции взамен π₁ на плоскость перпендикулярную прямой t в положении линии уровня переводит ее в положение проецирующей прямой (рисунок 16).

Для этого введем еще одну дополнительную плоскость, представленную новой осью чертежа X₂, перпендикулярной t'₁. Для построения новой проекции линии сохраняем координаты плоскости π₁. 

Решить на комплексном чертеже самостоятельно следующие задачи по теме "Преобразование чертежа". 

5.1 Определить, используя перемену плоскостей проекций, длину отрезка прямой ν (рисунок 17).

5.2 Найти расстояние от точки A до прямой общего положения t (рисунок 17).

При необходимости определения расстояния от точки до плоскости общего положения достаточно плоскость перевести в положение проецирующей. Это может быть достигнуто за счет переориентации линий уровня плоскости, перевода их в положение проецирующих прямых.

Рисунок 17

Пример решения задачи. Для решения задачи поступаем следующим образом:

1)выделим (проведем) в плоскости линию (рисунок 18) уровня, для определенности фронталь f;

Рисунок 18 - Расстояние от точки до плоскости

2)введем новую плоскость, перпендикулярную фронтали (новая ось чертежа X₁ );

3)изобразим на новой плоскости проекций стороны треугольника и точки A . Перпендикуляр A'₁S'₂ и определит искомое расстояние от точки до плоскости.

Рассмотренный подход является наиболее общим для решения подобного рода метрических задач.

5.3 Определить расстояние от точки A до плоскости DCB, плоскости Р (рисунок 19).

5.4 Определить угол наклона плоскости DBC к фронтальной плоскости проекции и угол наклона плоскости P к горизонтальной плоскости проекции (рисунок 19).

5.5 Через точку A провести прямую перпендикулярную плоскости треугольника BCD (рисунок 19).

Рисунок 19

5.6 Через точку A провести плоскость перпендикулярную плоскости треугольника BCD (рисунок 19).

5.7 Определить площадь треугольного отсека BCD(рисунок 19).

5.8 Найти, с помощью перемены плоскостей проекции точку пересечения прямой и плоскости (задача 3.8).

5.9 Определить величину двугранного угла образованного пересечение плоскостей P и Q (задача 3.6).

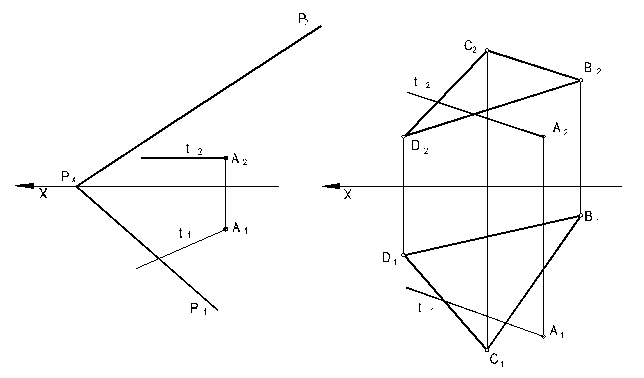
5.10 Определить угол наклона прямой t к плоскостям BCD иР (рисунок 20). 

6 Кривые линии

Кривые в трехмерном пространстве являются результатом пересечения поверхностей. Если в качестве одной из них выступает плоскость, то получается плоская кривая. Вследствие их одномерности все, что было ранее определено для прямых, может быть обобщено и на кривые.

Существенным является то, что ортогональное проецирование сохраняет положение касательной, т.е. если t касательная к кривой 1 то t₁ ( t₂ ) будут касательными к 1_l ( 1₂).

6.1 Построить эллипс по двум диаметрам ( Dгор = 80 , Dвер = 50 ).

6.2 Построить окружность R = 30, лежащую в плоскости общего положения P (задача 3.8).

6.3 По предложенным точкам построить с помощью радиусо -графического метода составную кривую (обвод).

6.4 Построить дугу параболы, заданную граничными точками A и B, и касательными в них . Построить дугу параболы, заданную тремя точками (рисунок 21).

Рисунок 21

6.5 Построить сопряжения двух окружностей ( R₁ = 40, R₂ = 20, O₁O₂ = 80 ) прямой линией, третьей окружностью (касание внешнее и внутреннее).