Пределы на бесконечности

Кроме предела в точке , можно рассматривать предел в точке, бесконечно удаленной в сторону или . В этом случае понятие предела необходимо уточнить.

Говорят, что предел функции при равен , если для существует такое, что для , удовлетворяющего условию , выполняется неравенство . Аналогично, при , если для существует такое, что для , , выполняется неравенство .

Если функция , где и есть суммы одночленов от переменной то предел отношения при или равен пределу отношения старших членов (т.е. членов с наибольшими степенями переменной функций и ).

Пример 3. , поскольку для выполнено неравенство , если только

Пример 4.

.

Пример 5.

.

Бесконечные пределы

Функция называется бесконечно малой при (или , или ) если для сколь угодно малого положительного числа найдется такое положительное число (), что для всех будет верно неравенство .

При () функция называется бесконечно малой, если для сколь угодно малого положительного числа найдется такое положительное число , что для всех будет верно неравенство .

Предел бесконечно малой величины в точке сгущения (или на бесконечности) равен нулю, т.е. .

Теорема: Если функция , определенная на множестве имеет предел в точке сгущения (или на бесконечности), то её можно представить в виде суммы этого числа и бесконечно малой величины: .

Справедлива также и обратная теорема: Если функцию , определенную на множестве , можно представить в точке сгущения (или на бесконечности) в виде суммы числа и бесконечно малой величины : то число является пределом этой функции при указанных условиях.

Свойства бесконечно малых величин:

• Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая;

• Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая;

• Частное от деления бесконечно малой на функцию, предел которой отличен от нуля, есть величина бесконечно малая.

Функция называется бесконечно большой при (или , или ) если для сколь угодно большого положительного числа найдется такое положительное число (), что для всех будет верно неравенство .

При () функция называется бесконечно большой, если для сколь угодно большого положительного числа найдется такое положительное число , что для всех будет верно неравенство .

Предел бесконечно большой величины в точке сгущения (или на бесконечности) равен бесконечности, т.е. .

Свойства бесконечно больших величин:

• Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая;

• Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая;

• Частное от деления бесконечно большой величины на функцию, имеющую предел в точке есть величина бесконечно большая.

Теорема. Если функция есть бесконечно малая величина при () то функция есть бесконечно большая величина при ().

Обратная теорема. Если функция есть бесконечно большая величина при () то функция есть бесконечно малая величина при ().

Сравнение бесконечно малых величин:

• Две бесконечно малые величины и называются бесконечно малыми одного порядка, если предел их отношения есть конечное число, отличное от нуля, т.е. ;

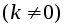• Величина называется бесконечно малой величиной высшего порядка по сравнению с , если предел отношения к равен нулю, т.е.;

• Величина называется бесконечно малой величиной низшего порядка по сравнению с , если предел отношения к является бесконечно большой величиной, т.е.;

• Две бесконечно малые величины 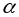и называются эквивалентными бесконечно малыми, если предел их отношения равен единице, т.е. .

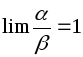Пользуясь приведенными выше теоремами, которые устанавливают взаимосвязь между бесконечно малыми и бесконечно большими величинами, можно распространить эти свойства на бесконечно большие величины.

Решение задачи сравнения бесконечно малых (бесконечно больших) величин связано с необходимостью корректно раскрыть неопределенность . Методы раскрытия этой и других неопределенностей будут подробно рассмотрены позднее.

Если и , то

Если и при а для близких к (т.е. ограничена в окрестности точки ), то .

Пример 8. , т.к. , а

Пример 9. т.к. и при .