
- •Функции Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
Понятие числовой последовательности
Числовой последовательностью называется числовая функция, определенная на множестве натуральных чисел.
Если
функцию
![]() задать на множестве натуральных чисел
задать на множестве натуральных чисел
![]() ,
то множество значений функции будет
счетным и каждому номеру
,
то множество значений функции будет
счетным и каждому номеру
![]() ставится в соответствие число
ставится в соответствие число
![]() .
В этом случае говорят, что задана числовая
последовательность.
Числа
.
В этом случае говорят, что задана числовая
последовательность.
Числа
![]() называют элементами
или членами последовательности, а число
называют элементами
или членами последовательности, а число
![]() – общим или
– общим или
![]() –м
членом последовательности. Каждый
элемент
–м
членом последовательности. Каждый
элемент
![]() имеет последующий элемент
имеет последующий элемент
![]() .
Это объясняет употребление термина
«последовательность».
.
Это объясняет употребление термина
«последовательность».
Задают
последовательность обычно либо
перечислением ее элементов
![]() ,
либо указанием закона, по которому
вычисляется элемент с номером
,
либо указанием закона, по которому
вычисляется элемент с номером
![]() ,
т.е. указанием формулы ее
,
т.е. указанием формулы ее
![]() ‑го
члена
‑го
члена
![]() .
.
Пример.
Последовательность
![]() может быть
задана формулой:
может быть
задана формулой:
![]() .
.
Обычно
последовательности обозначаются так:
![]() и т.п., где в скобках указывается формула
ее
и т.п., где в скобках указывается формула
ее
![]() -го
члена.
-го
члена.
Пример.
Последовательность
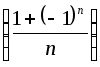 ‑ это
последовательность
‑ это
последовательность
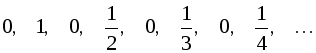
Множество
всех элементов последовательности
![]() обозначается
обозначается
![]() .
.
Пусть
![]() и
и
![]() ‑ две последовательности.
‑ две последовательности.
Суммой
последовательностей
![]() и
и
![]() называют последовательность
называют последовательность
![]() ,
где
,
где
![]() ,
т.е.
,
т.е.
![]() .
.
Разностью
этих последовательностей называют
последовательность
![]() ,
где
,
где
![]() ,
т.е.
,
т.е.
![]() .
.
Если
![]() и
и
![]() ‑ постоянные,
то последовательность
‑ постоянные,
то последовательность
![]() ,
,
![]() называют линейной
комбинацией
последовательностей
называют линейной
комбинацией
последовательностей
![]() и
и
![]() ,
т.е.
,
т.е.
![]() .
.
Произведением
последовательностей
![]() и
и
![]() называют последовательность с
называют последовательность с
![]() -м
членом
-м
членом
![]() ,
т.е.
,
т.е.
![]() .
.
Если
![]() ,
то можно определить частное
,
то можно определить частное
 .
.
Сумма,
разность, произведение и частное
последовательностей
![]() и
и
![]() называются их алгебраическими
композициями.
называются их алгебраическими
композициями.
Пример.
Рассмотрим
последовательности
![]() и
и
![]() ,
где
,
где
![]() .
Тогда
.
Тогда
![]() ,
т.е. последовательность
,
т.е. последовательность
![]() имеет все элементы, равные нулю.
имеет все элементы, равные нулю.
![]() ,
,
 ,
т.е. все элементы произведения и частного
равны
,
т.е. все элементы произведения и частного
равны
![]() .
.
Если
вычеркнуть некоторые элементы
последовательности
![]() так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемую
подпоследовательностью
последовательности
так, чтобы осталось бесконечное множество
элементов, то получим другую
последовательность, называемую
подпоследовательностью
последовательности
![]() .
Если вычеркнуть несколько первых
элементов последовательности
.
Если вычеркнуть несколько первых
элементов последовательности
![]() ,
то новую последовательность называют
остатком.
,
то новую последовательность называют
остатком.
Последовательность
![]() ограничена
сверху
(снизу),
если множество
ограничена
сверху
(снизу),
если множество
![]() ограничено сверху (снизу). Последовательность
называют ограниченной,
если она ограничена сверху и снизу.
Последовательность ограничена тогда
и только тогда, когда ограничен любой
ее остаток.
ограничено сверху (снизу). Последовательность
называют ограниченной,
если она ограничена сверху и снизу.
Последовательность ограничена тогда
и только тогда, когда ограничен любой
ее остаток.
Сходящиеся последовательности
Говорят,
что последовательность
![]() сходится, если существует число
сходится, если существует число
![]() такое, что для любого
такое, что для любого
![]() существует такое
существует такое
![]() ,
что для любого
,
что для любого
![]() ,
выполняется неравенство:
,
выполняется неравенство:
![]() .
.
Число
![]() называют пределом
последовательности
называют пределом
последовательности
![]() .
При этом записывают
.
При этом записывают
![]() или
или
![]() .
.
Пример.
 .
.
Покажем,
что
![]() .
Зададим любое число
.
Зададим любое число
![]() .
Неравенство
.
Неравенство
 выполняется для
выполняется для
![]() ,
такого, что
,
такого, что
 ,
что определение сходимости выполняется
для числа
,
что определение сходимости выполняется
для числа
![]() .
Значит,
.
Значит,
![]() .
.
Иными
словами
![]() означает, что все члены последовательности
означает, что все члены последовательности
![]() с достаточно большими номерами мало
отличается от числа
с достаточно большими номерами мало
отличается от числа
![]() ,
т.е. начиная с некоторого номера
,
т.е. начиная с некоторого номера
![]() (при
(при
![]() )
элементы последовательности находятся
в интервале
)
элементы последовательности находятся
в интервале
![]() ,
который называется
,
который называется
![]() –окрестностью
точки
–окрестностью
точки
![]() .
.
Последовательность
![]() ,
предел которой равен нулю (
,
предел которой равен нулю (![]() ,
или
,
или
![]() при
при
![]() )
называется бесконечно
малой.
)
называется бесконечно
малой.
Применительно к бесконечно малым справедливы утверждения:
-
Сумма двух бесконечно малых является бесконечно малой;
-
Произведение бесконечно малой на ограниченную величину является бесконечно малой.
Теорема.
Для того
чтобы последовательность
![]() имела предел, необходимо и достаточно
чтобы
имела предел, необходимо и достаточно
чтобы
![]() ,
где
,
где
![]() – постоянная;
– постоянная;
![]() –
бесконечно малая.
–
бесконечно малая.
Основные свойства сходящихся последовательностей:
-
Сходящаяся последовательность имеет только один предел;
-
Сходящаяся последовательность ограничена;
-
Если
 ,
то
,
то
 ;
; -
При любых постоянных
 и
и

 ;
; -
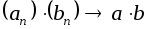 ;
; -
Если
 ,
,
 и
и
 ,
то
,
то
 ;
; -
Если
 ,
то
,
то
 ;
; -
Если
 и
и
 ,
то
,
то
 ;
; -
Если
 ,
то
,
то
 .
.
Свойства 3. и 4. обобщаются на случай любого числа сходящихся последовательностей.
Отметим,
что при вычислении предела дроби,
числитель и знаменатель которой
представляют собой линейные комбинации
степеней
![]() ,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
,
предел дроби равен пределу отношения
старших членов (т.е. членов, содержащих
наибольшие степени
![]() числителя и знаменателя).
числителя и знаменателя).
Последовательность
![]() называется:
называется:
-
возрастающей, если
 ;
; -
строго возрастающей, если
 ;
; -
убывающей, если
 ;
; -
строго убывающей, если
 .
.
Все такие последовательности называют монотонными.
Теорема.
Если
последовательность
![]() монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
монотонно возрастает и ограничена
сверху, то она сходится и ее предел равен
ее точной верхней грани; если
последовательность убывает и ограничена
снизу, то она сходится к своей точной
нижней грани.
