
- •Функции Основные понятия
- •Понятие числовой последовательности
- •Сходящиеся последовательности
- •Бесконечный предел
- •Замечательные пределы
- •Принцип сходимости
- •Предел функции. Теорема Гейне
- •Односторонние пределы
- •Пределы на бесконечности
- •Бесконечные пределы
- •Непрерывность функции
- •Непрерывность композиции
- •Точки разрыва
Размещено на http://www.allbest.ru/
Функции Основные понятия
При изучении различного рода явлений приходится иметь дело с совокупностью переменных величин, которые связаны между собой таким образом, что значения одних величин, (независимых переменных), полностью определяют значения других (зависимых переменных). В этом случае говорят о функциональной зависимости между переменными. Функция или функциональная зависимость – одно из основных математических понятий, при помощи которого моделируются взаимосвязи между различными величинами. Понятие функции, как и понятие множества, относится к числу начальных математических категорий, однако функции можно дать достаточно точное определение.
Пусть
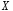 ‑ некоторое числовое множество и
пусть задан закон (правило)
‑ некоторое числовое множество и
пусть задан закон (правило)
![]() ,
по которому каждому числу
,
по которому каждому числу
![]() ставится в соответствие единственное
число
ставится в соответствие единственное
число
![]() ,
обозначаемое
,
обозначаемое
![]() .
Тогда говорят, что на множестве
.
Тогда говорят, что на множестве
![]() задана функция
задана функция
![]() и записывают:
и записывают:
![]() или
или
![]() Чаще используют более простую терминологию:
задана функция
Чаще используют более простую терминологию:
задана функция
![]() ,
,
![]() .
.
Множество
![]() называют областью
определения
функции
называют областью
определения
функции
![]() .
Множество
.
Множество
![]() называют множеством
значений
функции
называют множеством
значений
функции
![]() .
При этом
.
При этом
![]() называют независимой
переменной
или аргументом функции,
называют независимой
переменной
или аргументом функции,
![]() – зависимой
переменной
или значением функции, а
– зависимой
переменной
или значением функции, а
![]() – характеристикой
функции.
Для обозначения функциональной
зависимости можно употреблять любую
другую букву (
– характеристикой
функции.
Для обозначения функциональной
зависимости можно употреблять любую
другую букву (![]() ,
,
![]() ,
,
![]() ,
,
![]() и т.д.). Частное значение функции
и т.д.). Частное значение функции
![]() при
при
![]() записывается как
записывается как
![]() .
.
Существуют аналитический, графический, табличный и др. способы задания функции.
При
аналитическом
способе зависимость между переменными
определяется формулами. Если при этом
множество
![]() не указано, то считают, что функция
задана в естественной области определения,
т.е. на таком множестве, где эти формулы
имеют смысл.
не указано, то считают, что функция
задана в естественной области определения,
т.е. на таком множестве, где эти формулы
имеют смысл.
При
графическом
способе задания функции зависимость
между переменными отражается с помощью
графика. Графиком функции на плоскости
![]() называется геометрическое место точек
называется геометрическое место точек
![]() ,
координаты которых связаны функциональной
зависимостью.
,
координаты которых связаны функциональной
зависимостью.
При табличном способе задания функции выписываются в определенном порядке значения аргумента и соответствующие значения функции. Таблица дает не все значения функции, причем промежуточные значения функции могут быть найдены лишь приближенно при решении интерполяционной задачи. Поэтому в общем случае найти точное аналитическое выражение функции по ее табличным данным нельзя. Однако всегда можно построить интерполяционную формулу, и притом не одну (например, многочлен Лагранжа), которая для значений аргумента, имеющихся в таблице, будет давать соответствующие табличные значения функции.
Функции характеризуются рядом свойств, к важнейшим из которых относятся: четность, нули, периодичность, ограниченность, монотонность функции, а также наличие у функции асимптот и обратной функции:
-
Функция
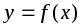 называется четной,
если для любого значения ее аргумента
из области определения выполняется
равенство
называется четной,
если для любого значения ее аргумента
из области определения выполняется
равенство
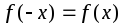 .
Сумма, разность и произведение четных
функций есть функция четная;
.
Сумма, разность и произведение четных
функций есть функция четная; -
Функция
 называется нечетной,
если для любого значения аргумента из
области ее определения выполняется
равенство
называется нечетной,
если для любого значения аргумента из
области ее определения выполняется
равенство
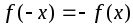 .
Сумма и разность нечетных функций есть
функция нечетная, а частное и произведение
нечетных функций – функция четная;
.
Сумма и разность нечетных функций есть
функция нечетная, а частное и произведение
нечетных функций – функция четная; -
Нулями функции
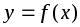 называют значения аргумента, при которых
функция обращается в ноль. Графически
нулями функции являются точки пересечения
графика функции с осью абсцисс;
называют значения аргумента, при которых
функция обращается в ноль. Графически
нулями функции являются точки пересечения
графика функции с осью абсцисс; -
Функция
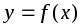 называется периодической,
если существует число
называется периодической,
если существует число
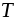 такое, что для каждого значения аргумента
такое, что для каждого значения аргумента
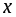 из области ее определения выполняется
равенство
из области ее определения выполняется
равенство
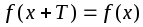 .
Число
.
Число
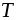 называют периодом
этой функции;
называют периодом
этой функции; -
Функция
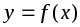 называется возрастающей
на некотором промежутке, если для любых
значений
называется возрастающей
на некотором промежутке, если для любых
значений
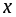 из этого промежутка, большему
значению аргумента соответствует
большее
значение функции, т.е.
из этого промежутка, большему
значению аргумента соответствует
большее
значение функции, т.е.
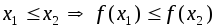 .
Функция
.
Функция
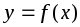 называется убывающей
на некотором промежутке, если для любых
значений
называется убывающей
на некотором промежутке, если для любых
значений
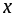 из этого промежутка, большему
значению аргумента соответствует
меньшее значение функции, т.е.
из этого промежутка, большему
значению аргумента соответствует
меньшее значение функции, т.е.
 .
Как возрастающие, так и убывающие
функции называются монотонными;
.
Как возрастающие, так и убывающие
функции называются монотонными; -
Асимптотой графика функции называется прямая, к которой сколь угодно близко приближается график данной функции при стремлении аргумента к бесконечности (горизонтальная и наклонная асимптоты), или к некоторому числу
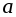 (вертикальная асимптота);
(вертикальная асимптота); -
Функция
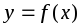 называется ограниченной
сверху
(снизу),
если существует число
называется ограниченной
сверху
(снизу),
если существует число
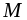 такое, что для каждого значения аргумента
такое, что для каждого значения аргумента
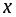 из области ее определения
из области ее определения
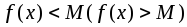 .
Функция
.
Функция
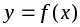 называется ограниченной,
если существует число
называется ограниченной,
если существует число
 такое, что для каждого значения аргумента
такое, что для каждого значения аргумента
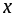 из области ее определения
из области ее определения
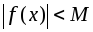 ;
; -
Функция
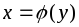 называется обратной
по отношению к
называется обратной
по отношению к
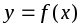 ,
если при подстановке её вместо аргумента
,
если при подстановке её вместо аргумента
 получается тождественное равенство:
получается тождественное равенство:
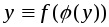 ;
; -
Если каждому значению переменной
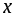 соответствует одно значение переменной
соответствует одно значение переменной
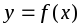 ,
то
,
то
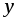 называется однозначной
функцией от
называется однозначной
функцией от
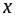 ;
если хотя бы некоторым значениям
переменной
;
если хотя бы некоторым значениям
переменной
 соответствует несколько (два, три или
бесконечное множество) значений
соответствует несколько (два, три или
бесконечное множество) значений
 ,
то
,
то
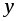 называется многозначной
(двузначной, трехзначной и т.д.) функцией
от
называется многозначной
(двузначной, трехзначной и т.д.) функцией
от
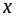 .
.
