7. Графический метод решения задачи злп

Найдем наибольшее значение линейной функции графическим методом.

L = 

x₁

- x₂

при следующих ограничениях

x₁

+ x₂

3

x₁

+ x₂

7

x₂

1

x₂

5

x₁

4

Решение :

В первую очередь, найдем область допустимых значений, т.е. точки x₁ и x₂ , которые удовлетворяют системе ограничений. По условию задачи x₁ 0, x₂ 0 ,т.е. мы рассматриваем только те точки , которые принадлежат первой четверти.

Рассмотрим неравенство 1 системы ограничений.

x₁

+ x₂

3 

Преобразуем неравенство следующим образом .

x₁

+

x₂

3

1

1

Каждый член неравенства разделим на 3 .

x₁

+

x₂

1

3

3

Теперь мысленно заменим знак неравенства на знак равенства. Получим уравнение прямой в отрезках. На оси X₁ рисуем точку с координатой 3 . На оси X₂ рисуем точку с координатой 3 . Соединяем полученные точки и получаем необходимую прямую. Теперь возникает вопрос, какие точки мы должны принять к рассмотрению, лежащие выше или ниже построенной нами прямой.

В нашем случае знаменатель второго слагаемого равный 3 - положительный и знак неравенства больше или равен нулю, то есть нас интересуют точки лежащие выше нашей построенной прямой.

Объединим полученную полуплоскость с ранее найденными ограничениями, получим рисунок приведенный ниже.

Область допустимых значений выделена штриховкой.

A ( 3 , 0 )

B ( 0 , 3 )

Рассмотрим неравенство 2 системы ограничений.

x₁

+ x₂

7 

Преобразуем неравенство следующим образом .

x₁

+

x₂

7

1

1

Каждый член неравенства разделим на 7 .

x₁

+

x₂

1

7

7

Теперь мысленно заменим знак неравенства на знак равенства. Получим уравнение прямой в отрезках. На оси X₁ рисуем точку с координатой 7 . На оси X₂ рисуем точку с координатой 7 . Соединяем полученные точки и получаем необходимую прямую. Теперь возникает вопрос, какие точки мы должны принять к рассмотрению, лежащие выше или ниже построенной нами прямой.

В нашем случае знаменатель второго слагаемого равный 7 - положительный и знак неравенства меньше или равен нулю, то есть нас интересуют точки лежащие ниже нашей построенной прямой.

Объединим полученную полуплоскость с ранее найденными ограничениями, получим рисунок приведенный ниже.

Область допустимых значений выделена штриховкой.

A ( 3 , 0 )

B ( 7 , 0 )

C ( 0 , 3 )

D ( 0 , 7 )

Рассмотрим неравенство 3 системы ограничений.

x₂

1 

Мысленно заменим знак неравенства на знак равенства. Получим уравнение прямой параллельной оси x₁.

Нас интересуют точки лежащие выше построенной нами прямой.

Объединим полученную полуплоскость с ранее найденными ограничениями, получим рисунок приведенный ниже.

Область допустимых значений выделена штриховкой.

A ( 0 , 3 )

B ( 0 , 7 )

C ( 2 , 1 )

D ( 6 , 1 )

Рассмотрим неравенство 4 системы ограничений.

x₂

5 

Мысленно заменим знак неравенства на знак равенства. Получим уравнение прямой параллельной оси x₁.

Нас интересуют точки лежащие ниже построенной нами прямой.

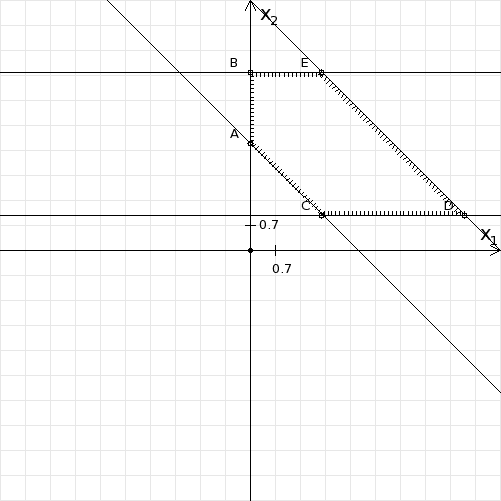
Объединим полученную полуплоскость с ранее найденными ограничениями, получим рисунок приведенный ниже.

Область допустимых значений выделена штриховкой.

A ( 0 , 3 )

B ( 0 , 5 )

C ( 2 , 1 )

D ( 6 , 1 )

E ( 2 , 5 )

Рассмотрим неравенство 5 системы ограничений.

x₁

4 

Мысленно заменим знак неравенства на знак равенства. Получим уравнение прямой параллельной оси x₂.

Нас интересуют точки лежащие левее построенной нами прямой.

Объединим полученную полуплоскость с ранее найденными ограничениями, получим рисунок приведенный ниже.

Область допустимых значений выделена штриховкой.

A ( 0 , 3 )

B ( 0 , 5 )

C ( 2 , 1 )

D ( 2 , 5 )

E ( 4 , 3 )

F ( 4 , 1 )

Вернемся к нашей исходной функции L .

L = 

x₁

- x₂

Допустим значение функции L равно 1 ( абсолютно произвольно выбранное число), тогда

1 = 

x₁

- x₂

А это выражение есть ничто иное , как уравнение прямой на плоскости. Из курса аналитической геометрии известно, что данная прямая перпендикулярна вектору , координатами которого являются коэффициенты функции, а именно вектору ON ( 1 , -1 ).

Следовательно, с геометрической точки зрения, наша исходная функция L изображается как множество прямых перпендикулярных вектору ON ( 1 , -1 ) .

Построим вектор ON ( 1 , -1 ), где координаты вектора равны коэффициентам исследуемой нами функции. В принципе, нас интересует только направление вектора ON. Поэтому, исключительно для большей наглядности, умножим координаты вектора ON на положительное число 21/5 ( взято произвольно ). При умножении координат на одно и тоже положительное число, как вы понимаете, направление вектора не меняется.

На рисунке ниже вектор ON ( 21/5 , -21/5 ) изображен красным цветом.

Причем очевидно, что значение функции будет возрастать при перемещении прямой в направлении вектора ON ( 21/5 , -21/5 ) . Это не значит , что диапазон перемещения прямой от точки O до точки N . А именно в направлении от точки O к точке N.

Будем перемещать прямую, перпендикулярную вектору ON, до тех пор, пока она полностью не пройдет область допустимых решений.

В нашем случае касание прямой , перед выходом из области допустимых решений, произойдет в точке F ( 4 , 1 ) . В данной точке значение нашей функции будет наибольшим.

Ответ :

Наибольшее значение функция достигает при x₁ = 4 x₂ = 1.

Значение функции : L = 3