§13.2 Некоторые физические свойства и параметры мембран

Измерение подвижности молекул мембраны и диффузии частиц через мембрану свидетельствует о том, что билипидный слой ведет

себя подобно жидкости. С другой стороны, мембрана есть упоря­доченная структура. Эти два фактора заставляют думать, что фос-фолипиды в мембране при ее естественном функционировании на­ходятся в жидкокристаллическом состоянии (см.§ 10.2). Жидкостные свойства мембраны подтверждаются методами ЭПР (см. § 30.3) и ЯМР (см. § 30.4).

Вязкость липидного слоя мембран приблизительно на два порядка выше вязкости воды, она равна 30-100 мПа-с, что соответствует примерно вязкости растительного масла. Поверхностное натяжение на 2-3 порядка ниже (0,03-1 мН/м), чем у воды.

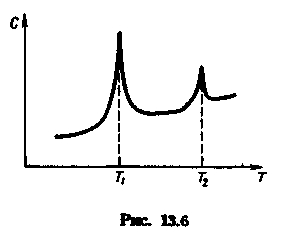
При изменении температуры в мембране можно наблюдать фазо­вые переходы: плавление липидов при нагревании и кристаллиза­цию при охлаждении. Фазовые переходы связаны с изменением энергии и поэтому могут быть обнаружены, в частности, по увели­чению теплоемкости с при изменении температуры (рис. 13.6; при температурах ti и Т₂ - фазовые переходы). Жидкокристаллическое состояние бислоя имеет меньшую вязкость и большую раствори­мость различных веществ, чем твердое состояние. Толщина жидко­кристаллического биослоя меньше, чем •^ердого.

Конформация (структура) молекул в жидком и твердом состоя­ниях различна, в чем можно убедиться при рентгеноструктурном анализе (см. § 24.7). В жидкой фазе молекулы фосфолипидов могут образовывать полоски (<кинки>), в которые способны внедряться молекулы диффундирующего вещества.

Перемещение <кинка> в этом случае будет приводить к диф­фузии молекулы поперек мембраны (рис. 13.7, а, <5).

Двойной фосфолипидный слой уподобляет мембрану конденса­тору, электроемкость 1 мм^ мембраны составляет 5-13 нФ.

53. УРАВНЕНИЕ НЕРНСТА-ПЛАНКА. ПЕРЕНОС ИОНОВ ЧЕРЕЗ МЕМБРАНЫ

На мембране существует разность потенциалов, следовательно, в мембране имеется электрическое поле. Оно оказывает влияние на диффузию заряженных частиц (ионов и электронов). Между напряженностью поля и градиентом потенциала существует соотношение: Заряд иона равен Z_e. На один ион действует сила f =сила, действующая на 1 моль ионов, равна где F—постоянная Фарадея, F = еN_A. Скорость направленного движения ионов пропорциональна действующей силе: Поток ионов где с- мо­лярная концентрация ионов

Плотность потока найдем:

В общем случае перенос ионов определяется двумя факторами: неравномерностью их распределения, т. е. градиентом концентра­ции, и воздействием электрического поля: -уравнение Нернста —Планка.

Поверхностная мембрана клетки не одинаково проницаема для разных ионов. Кроме того, концентрация каких-либо определенных ионов различна по разные стороны мембраны, внутри клетки под­держивается наиболее благоприятный состав ионов. Эти факторы приводят к появлению в нормально функционирующей клетке разности потенциалов между цитоплазмой и окружающей средой (потенциал покоя).

Основной вклад в создание и поддержание потенциала покоя вносят ионы Na⁺, K⁺ и Сl^-. Суммарная плотность потока этих ионов с учетом их знаков равна В стационарном состоянии суммарная плотность потока равна ну­лю, т. е. число различных ионов, проходящих в единицу времени через мембрану внутрь клетки, равно числу выходящих из клетки через мембрану: J = 0.

уравнение Гольдмана - Хаджтна – Катца:•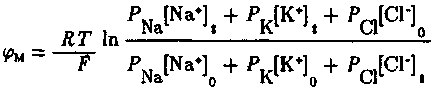

Различные концентрации ионов внутри и вне клетки созданы ионными насосами - системами активного транспорта. Можно ска­зать, что потенциал покоя обязан активному переносу. Проницаемость ионов существенно зависит от состояния организма.

Из уравнения Гольдмана-Ходжкина-Катца можно получить уравнение Нернста для равновесного состояния. При этом следует пренебречь проницаемостями всех ионов, кроме ионов одного сорта. Тогда для ионов К⁺

54. 1.2 Стационарный потенциал Гольдмана - Ходжкина

Для количественного описания потенциала в условиях проницаемости мембраны для нескольких ионов Ходжкин и Катц использовали представление о том, что потенциал покоя на равновесный, а стационарный по своей природе, то есть он отражает состояние системы, когда через мембрану непрерывно идут встречные потоки ионов K⁺, Na⁺, Cl^- и других.

Суммарный поток положительно заряженных частиц через мембраны равен сумме потоков одновалентных катионов минус сумма потоков одновалентных анионов.

Основной вклад в суммарный поток зарядов практически во всех клетках вносят ионы Na⁺, K⁺ и Cl^-, поэтому

Наличие суммарного потока приведет к изменению потенциала на мембране; скорость этого изменения зависит от емкости мембраны. Связь между плотностью тока j , удельной емкостью С и потенциалом j (В) известна из курса физики:

где - скорость изменения потенциала . При этом величина плотности тока " j " связана с плотностью потока одновалентных катионов Ф, соотношением j = Ф  F, где F - число Фарадея.

Уравнение потенциала для трех ионов имеет следующий вид:

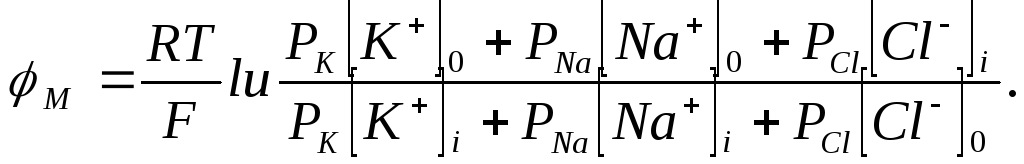
(P - проницаемость)

Это уравнение называется уравнением стационарного потенциала Гольдмана - Ходжкина - Катца.