
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
Понятие о диаграммах направленности
Из
соотношений (1.85) и (1.86) для векторов поля
в дальней зоне видно, что угловое
распределение составляющих векторов
E
и H
характеризуется функциями
![]() и
и
![]() ,
зависящими от угловых координат
,
зависящими от угловых координат
![]() и
и
![]() .
Эти функции называются диаграммами
направленности по полю для соответствующих
компонент электрического вектора,
возбуждаемого заданной системой токов.
Поскольку в общем случае
.
Эти функции называются диаграммами
направленности по полю для соответствующих
компонент электрического вектора,
возбуждаемого заданной системой токов.
Поскольку в общем случае
![]() и
и
![]() комплексны, они могут быть разбиты на
амплитудные и фазовые диаграммы
направленности. На практике обычно
используются амплитудные диаграммы
направленности
комплексны, они могут быть разбиты на
амплитудные и фазовые диаграммы
направленности. На практике обычно
используются амплитудные диаграммы
направленности
![]() и
и
![]() .
.
При наличии одновременно электрических и магнитных токов диаграммы направленности по полю определяются следующими соотношениями:
![]()
Помимо диаграмм направленности по полю, используется понятие диаграммы направленности по мощности, характеризующей угловое распределение излучаемой мощности.
Поток
мощности, излучаемый в направлении
![]() ,
,
![]() и отнесенный к единице телесного угла,
при наличии только электрических токов
пропорционален функции
и отнесенный к единице телесного угла,
при наличии только электрических токов
пропорционален функции
![]() ,
называемой диаграммой направленности
по мощности.
,
называемой диаграммой направленности
по мощности.
Поскольку парциальные мощности, вычисляемые по соответствующим компонентам векторов, аддитивны, можно считать, что
![]()
где
![]() и
и
![]() называются парциальными диаграммами
направленности по мощности.
называются парциальными диаграммами
направленности по мощности.
Для удобства графического изображения диаграмм направленности по полю и мощности их нормируют к единице, т.е. используют функции вида
![]() (1.87)
(1.87)
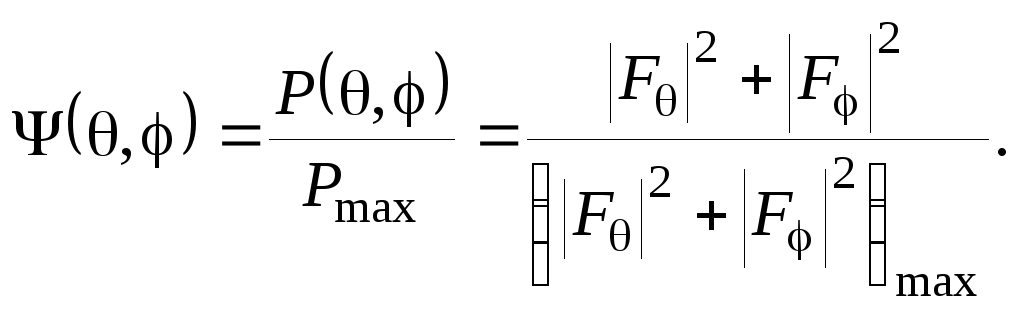 (1.88)
(1.88)
Для
оценки эффективности антенны вводится
коэффициент направленного действия
![]() ,
который показывает, во сколько раз
излучаемый в направлении
,
который показывает, во сколько раз
излучаемый в направлении
![]() ,
,
![]() поток мощности превышает поток мощности
в том же направлении от гипотетической
ненаправленной антенны, имеющей ту же
суммарную мощность излучения.
поток мощности превышает поток мощности
в том же направлении от гипотетической
ненаправленной антенны, имеющей ту же
суммарную мощность излучения.
В соответствии с определением
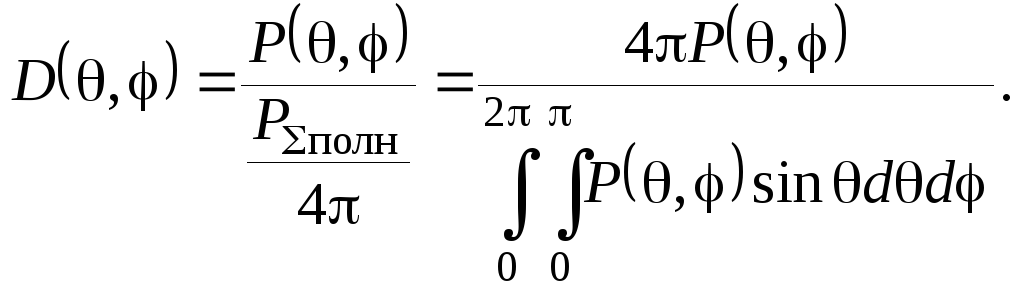 (1.89)
(1.89)
На
практике обычно представляет интерес
максимальное значение
![]()
 (1.90)
(1.90)
Поляризационные характеристики поля
Поляризационные характеристики - важнейшие характеристик излучаемого поля. Различают поля с линейной и эллиптической поляризациями.
При линейной поляризации вектор E в течение времени не изменяет своего пространственного расположения (изменяется лишь его направление на противоположное). При этом под плоскостью поляризации понимают плоскость, проходящую через вектор E и вектор Пойнтинга П, определяющий направление распространения волны (рис.1.9,а, где T – период колебания).
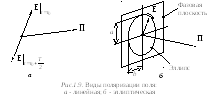 При
эллиптической поляризации (а также в
частном случае круговой) вектор E
изменяет свое направление в пространстве,
и его годограф описывает пространственную
периодическую кривую. Если спроектировать
годограф вектора на плоскость,
перпендикулярную вектору П
(фазовую
плоскость),
то получим в общем случае эллипс с
полуосями a
и b,
называемый поляризационным (рис.1.9,б).
При
эллиптической поляризации (а также в
частном случае круговой) вектор E
изменяет свое направление в пространстве,
и его годограф описывает пространственную
периодическую кривую. Если спроектировать
годограф вектора на плоскость,
перпендикулярную вектору П
(фазовую
плоскость),
то получим в общем случае эллипс с
полуосями a
и b,
называемый поляризационным (рис.1.9,б).
Эллиптическая
поляризация характеризуется коэффициентом
эллиптичности![]() ,
при этом в общем случае
,
при этом в общем случае
![]() .
В случае
.
В случае
![]() эллипс вырождается в окружность, и такая
поляризация называется круговой.
эллипс вырождается в окружность, и такая
поляризация называется круговой.
Если
направление вращения вектора E
соответствует правилу правого винта,
как показано на рис.1.9,б, эллиптически
поляризованное поле считается полем
правого вращения
![]() .
В противном случае эллиптически
поляризованное поле является полем
левого вращения
.
В противном случае эллиптически
поляризованное поле является полем
левого вращения
![]() .
.
