Часть I. Теория электромагнитного поля.

В разделе даны основные образы явлений, связанных с электромагнитным полем, в однородных средах и на границах раздела сред с разными характеристиками. Приведены основные характеристики сред, важные при проектировании высокочастотных устройств. Дана математическая форма записи указанных явлений и приведены некоторые математические приемы решения получаемых уравнений.

Все введенные в данном разделе понятия будут нами использоваться в последующих главах книги.

§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.

Все электромагнитные явления, относящиеся к макроскопической электродинамике, описываются уравнениями Максвелла, опубликованными в 1873 г. в знаменитом «Трактате об электричестве и магнетизме» [1]. Эта работа явилась обобщением всех накопленных к тому времени экспериментальных данных собранных Гауссом, Ампером, Фарадеем и многими другими. Для начинающих более пригоден исторический подход в изложении материала, т.к. он наиболее нагляден и прост. Однако, нами предполагается, что читатель уже прослушал курсы «общей физики» и «электротехники» и знаком с экспериментальными данными и их теоретической интерпретацией. В качестве хороших пособий для первоначального ознакомления можно порекомендовать следующие [4 - 6].

В данной книге уравнения Максвелла будут использоваться нами как средство для исследования электромагнитных явлений, свойства которых будут выведены из них, поэтому в начале мы постулируем эти уравнения. В международной системе Си они имеют следующий вид:

, (1.1а)

, (1.1б)

, (1.1в)

(1.1г)

При этом входящие в уравнения векторные величины имеют следующие размерности:

- напряженность электрического поля, В/м;

- напряженность магнитного поля, А/м;

- вектор электрической индукции, Кл/м²;

- вектор магнитной индукции, Вб/м² или Тл;

- объемная плотность магнитного тока (фиктивная величина), В/м²;

- объемная плотность электрического тока, А/м²;

- объемная плотность электрического заряда.

Источниками электромагнитного поля являются токи и , а также электрические заряды с объемной плотностью . Магнитный ток есть математическая абстракция, он в природе не существует, однако, его введение позволяет упростить вычисления поля при возбуждении колебаний поля в раскрывах антенн или волноводов. Поскольку ток есть движение электрических зарядов, то можно сказать, что электрические заряды являются единственными источниками электромагнитного поля (магнитные заряды пока не были обнаружены).

В вакууме существует простая связь между векторами магнитной и электрической индукции и векторами напряженностей магнитного и электрического полей соответственно:

, (1.2а)

, (1.2б)

здесь Гн/м – абсолютная магнитная проницаемость вакуума, Ф/м – абсолютная диэлектрическая проницаемость вакуума. В следующем разделе мы покажем, какое влияние вещество, в отличие от вакуума, оказывает на характер поля в нем.

Выражения (1.1а – 1.1г) не являются независимыми. Например, если взять дивергенцию от обеих частей уравнения (1.1а) и учесть, что дивергенция ротора равна нулю, можно получить:

,

а поскольку магнитные заряды отсутствуют, то , что приводит нас к выражению , т.е. к уравнению (1.1г). Если применить операцию дивергенции к уравнению (1.1б) и учесть тождество (1.1в), то можно получить уравнение непрерывности, выражающее закон сохранения заряда:

, (1.3)

т.е. поток вектора плотности электрического тока, в заданной точке пространства, определяется изменением объемной плотности электрического заряда в этой точке. Именно закон сохранения заряда навел Максвелла на мысль о необходимости введения тока смещения в уравнение (1.1б).

Как известно операция дифференцирования не может быть выполнена в областях, где параметры среды испытывают скачек, поэтому для описания подобного рода явлений применяют уравнения Максвелла в интегральной форме. Эти уравнения могут быть получены из уравнений (1.1а – 11.г), путем интегрирования последних, с применением известных тождеств векторного анализа. В частности применение теоремы Остроградского-Гаусса к уравнениям (1.1в) и (1.1г) дает

, (1.4)

, (1.5)

здесь Q – заряд, сосредоточенный в замкнутом поверхностью S объеме V. Применение же теоремы Стокса к уравнению (1.1а) приводит нас к уравнению

, (1.6)

которое без вектора представляет собой закон Фарадея и является основой для второго закона Кирхгофа. При этом в уравнении (1.6) C представляет собой замкнутый контур, охватывающий поверхность S, как показано на рис. 1.1.

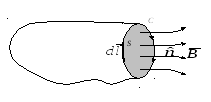
Рис.1.1. Поток магнитной индукции через поверхность S.

Закон Ампера может быть получен путем применения теоремы Стокса в уравнению (1.1б):

, (1.7)

где полный электрический ток через поверхность S.

Представленные уравнения справедливы для переменных полей любого вида, однако, в данном пособии мы будем рассматривать гармонические поля в установившемся режиме. В этом случае очень удобно использовать метод комплексных амплитуд, в котором зависимость от времени описывается множителем . Рассмотрим данный метод.

Пусть колебание электрического поля, происходящее в направлении оси x, имеет следующий вид

, (1.8)

где A действительная амплитуда сигнала,  - круговая частота,  - начальная фаза сигнала в момент времени , тогда с применением метода комплексных амплитуд можно записать:

. (1.9)

При этом

. (1.10)

Если же колебания электрического поля имеют составляющие вдоль всех осей:

, (1.11)

то с помощью комплексных амплитуд можно записать

, (1.12)

Во многих задачах требуется рассчитать среднюю мощность или энергию электромагнитного поля. Как известно эти величины пропорциональны квадрату напряженности поля и для гармонических колебаний мы можем записать:

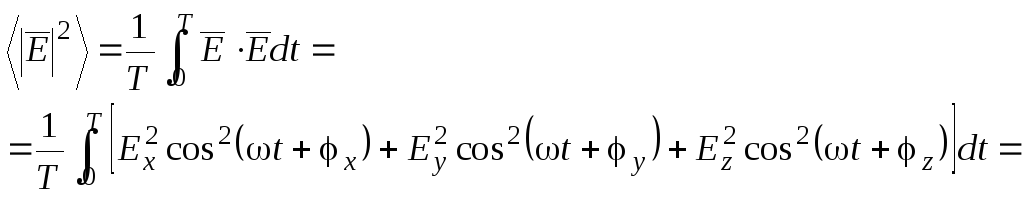
(1.13)

В результате для комплексных амплитуд уравнения Максвелла приобретут следующий вид:

, (1.14а)

, (1.14б)

, (1.14в)

(1.14г)

При этом преобразование Фурье может быть использовано для обращения решения уравнений из частотной области во временную.

Величины и в уравнениях (1.14) являются объемными плотностями электрического и магнитного токов с размерностями А/м² и В/м² соответственно. Однако во многих задачах электродинамики настоящие источники электромагнитного поля могут быть заданы в виде поверхностных или линейных плотностей тока, или в виде диполей. В этом случае исходные величины можно преобразовать к объемным плотностям посредством дельта функций Дирака, как показано на рис. 1.2.

Р ис.1.2. Заданные объемные (а), поверхностные (б), линейные (в) токи и электрический и магнитный диполи (г)