§ 1.10. Важные теоремы

В заключение первой части рассмотрим некоторые важные теоремы электродинамики, часто применяемые при изучении поведения различных устройств СВЧ.

Принцип взаимности

Принцип (или теорема) взаимности является одним из важнейших инструментов для получения матриц СВЧ устройств и дальнейшего исследования свойств этих устройств, также теорема взаимности позволяет исследовать задачи возбуждения волноводов и антенн.

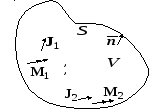
Рис. 1.20 К теореме взаимности

Итак, пусть в некотором объеме V, окруженном замкнутой поверхностью S, действуют независимые сторонние источники , и , , возбуждающие в рассматриваемом объеме поля , и , соответственно, как показано на рис.1.20. Запишем уравнения Максвелла для каждого набора источников:

, (1.170а)

, (1.170б)

, (1.171а)

. (1.171б)

Рассмотрим векторное тождество

.

Которое с учетом уравнений Максвелла (1.170) и (1.171) преобразуется к виду

. (1.172)

Интегрируя (1.172) по объему V и применяя теорему Остроградского – Гаусса, получим

. (1.173)

Уравнение (1.173) представляет собой теорему взаимности в общем виде. Однако на практике возможен ряд частных случаев, сильно упрощающих формулировку теоремы. Рассмотрим некоторые из них.

В объеме V отсутствуют сторонние источники. Тогда и поля , и , представляют собой свободные колебания электромагнитного поля. При этом правая часть равенства (1.173) обращается в ноль, и мы имеем

. (1.174)

Объем V окружен идеальным проводником. В этом случае поверхностный интеграл в (1.173) обращается в ноль, учитывая векторное тождество согласно граничные условия на поверхности идеального проводника - . В результате получим

. (1.175)

Соотношение (1.175) показывает, что поля, возбуждаемые первыми источниками, в области, занимаемой вторыми источниками, и наоборот, не изменятся, если поменять местами точки возбуждения и наблюдения. Т.е. сторонний ток возбуждает в области занимаемой током такое же поле , какое он возбуждал бы в месте своего расположения, будучи помещен на место тока , и наоборот.

Объем . В этом случае поверхностный интеграл обращается в ноль, поскольку на большом удалении от источников выполняется равенство , и можно получить

,

т.е. и в этом случае условие (1.175) выполняется. Данный результат имеет очень важное значение в теории антенн. Он позволяет утверждать, в частности, что если в радиолинии содержащей передающую и приемную антенны, приемную антенну заменить на передающую, а передающую - приемной, параметры радиолинии не изменятся.

Метод зеркальных отображений

Во многих задачах электродинамики источник электромагнитных волн расположен вблизи проводящей поверхности, размеры которой превосходят размеры источника. Метод зеркальных отображений позволяет убрать из рассмотрения проводящую плоскость посредством размещения мнимого источника электромагнитных волн с другой стороны от проводящей плоскости.

Рассмотрим в качестве источника волн поверхностный ток с плотностью расположенный параллельно проводящей поверхности, как показано на рис.1.21а.

Поскольку ток имеет бесконечные размеры и однороден в направлениях x и y, он возбуждает плоские электромагнитные волны, распространяющиеся вдоль оси z в обе стороны от него. Волна, распространяющаяся в направлении , отражается от проводящей поверхности при z = 0, и движется в противоположном направлении. Таким образом, в области образуется стоячая волна, а в области - существует бегущая волна.

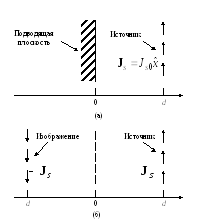
Рис.1.21. Иллюстрация применения метода зеркальных отображений: а) - поверхностный ток параллельный проводящей плоскости; б) замена проводящей плоскости мнимым источником тока.

В этом случае уравнения для полей могут быть представлены в следующем виде

, при , (1.176а)

, при , (1.176б)

, при , (1.177а)

, при . (1.177б)

Заметим, что стоячие волны в (1.176) записаны таким образом, чтобы удовлетворить граничному условию при z = 0. Кроме того, уравнения (1.176) и (1.177) должны удовлетворять условиям непрерывности электрического поля, т.к. , и неоднородности магнитного поля, связанной с наличием поверхностного электрического тока , при z = d. В результате получим

, (1.178а)

. (1.178б)

Подставляя (1.176) и (1.177) в (1.178), получим систему относительно A и B

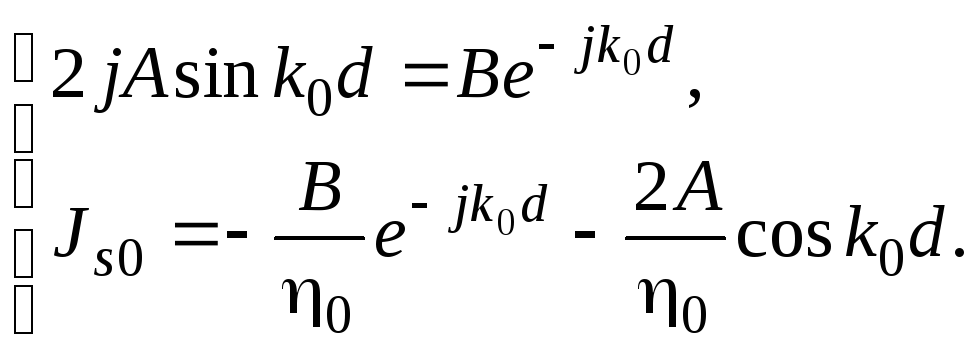
Решение данной системы дает следующие соотношения для A и B

,

.

, при , (1.179а)

, при , (1.179б)

, при , (1.180а)

, при . (1.180б)

Теперь рассмотрим решение той же задачи с применением метода зеркальных изображений. Как показано на рис.1.21 б, проводящая плоскость заменена воображаемым источником тока , помещенном при z = - d. Результирующее поле в области находится суперпозицией полей двух источников, которые могут быть найдены отдельно друг от друга:

- поля, порождаемые источником при z = d

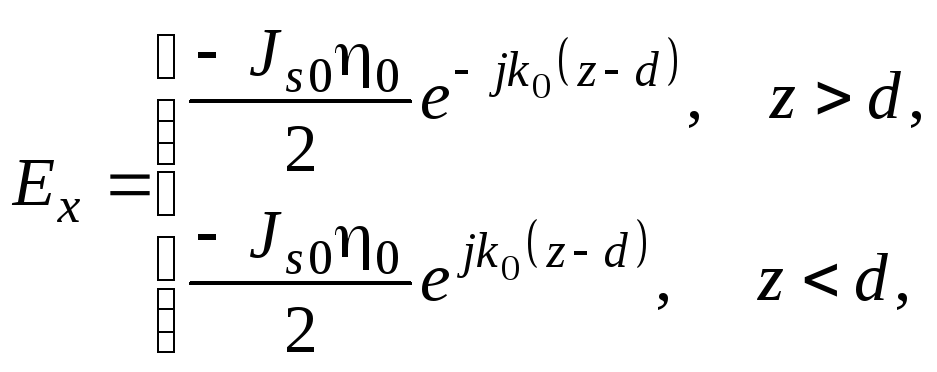(1.181а)

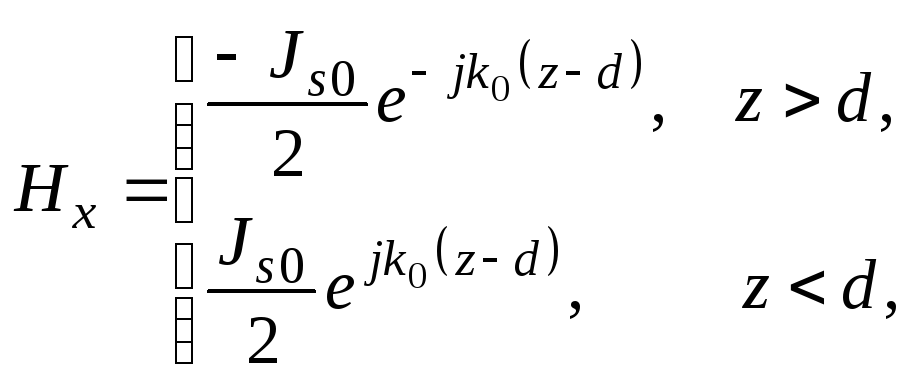(1.181б)

- поля, порождаемые источником при z = - d

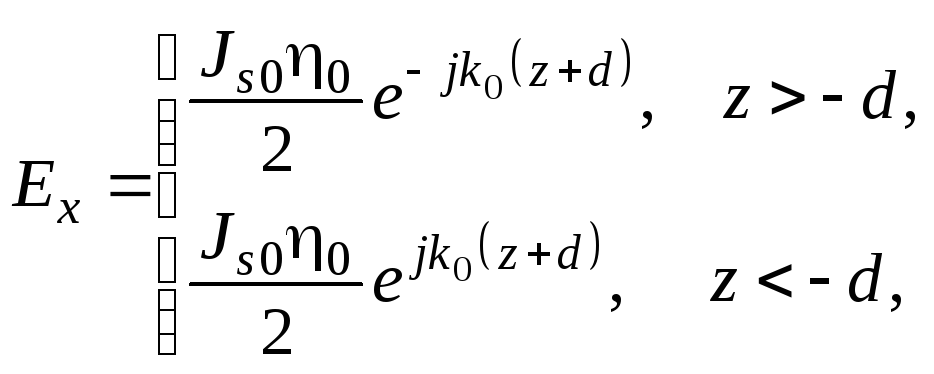(1.182а)

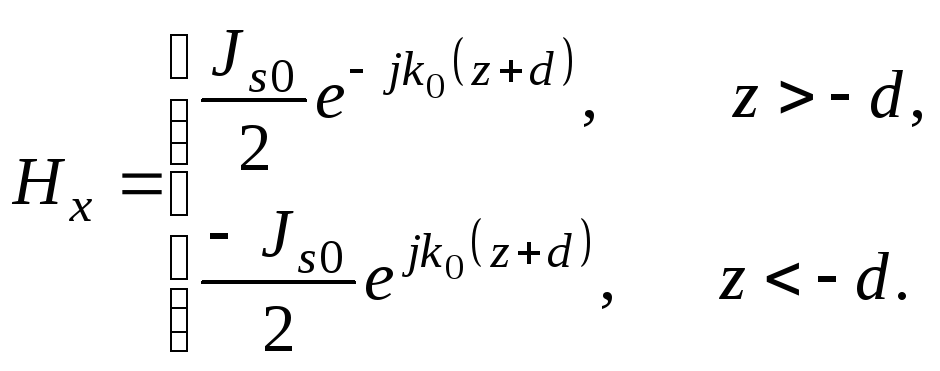(1.182б)

Суммирование (1.181) и (1.182) для каждой из компонент дает выражения (1.179) и (1.180).

На рис.1.22 представлены основные результаты применения метода зеркальных отображений для электрических и магнитных диполей.

Рис.1.22. Применение метода зеркальных изображений к электрическим (а и б) и магнитным (в и г) токам разной направленности