Понятие о поверхностном сопротивлении. Скин-эффект.

При создании многих устройств СВЧ (особенно в Ku и Ka-диапазонах частот) требуется учитывать потери в проводниках, вызываемые конечной проводимостью реальных проводников. Для расчета этих потерь очень удобно ввести понятие поверхностного сопротивления.

Как мы установили выше плоская волна, падающая на поверхность проводника с большой, но конечной проводимостью, большей частью отражается от границы раздела, а оставшаяся часть рассеивается внутри проводника на небольшом расстоянии от границы раздела сред. Рассчитаем мощность, рассеиваемую проводником. Используя вектор Пойнтинга, получим выражение

,

которое для хороших проводников, учитывая условие , преобразуется к виду

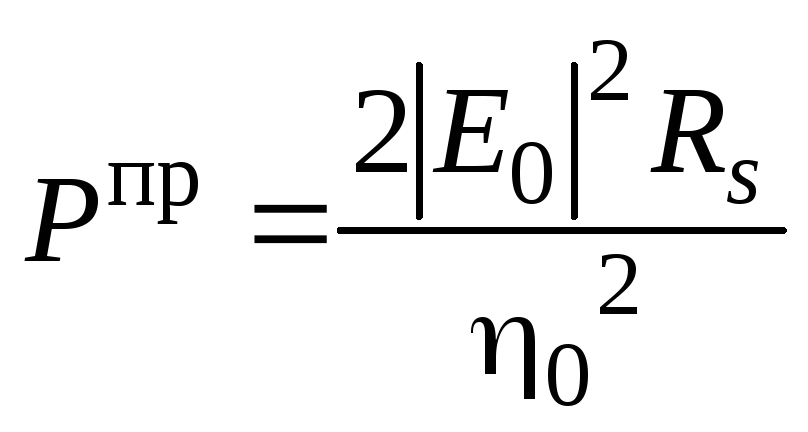, (1.148)

где - поверхностное сопротивление металла (неидеального проводника).

Применим закон Джоуля - Ленца для расчета прошедшей внутрь проводника мощности, используя понятие поверхностного сопротивления, поверхностного тока и его связи с напряженностью магнитного поля

(1.149)

Применение понятия поверхностного сопротивления для расчета потерь в проводниках вполне справедливо пока сохраняется соотношение , что для большинства металлов в СВЧ диапазоне выполняется, например, для меди на 1 ГГц , что существенно меньше .

§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения

Изучение поведения плоских волн на границе раздела продолжим рассмотрением случая падения плоской волны на границу раздела диэлектриков без потерь под произвольным углом к границе раздела, как показано на рис.1.19. Данная задача имеет два канонических решения: для вектора электрического поля, лежащего или в плоскости xz (параллельная поляризация), или перпендикулярно плоскости xz (перпендикулярная поляризация). Стоит заметить, что произвольно падающая плоская волна может иметь любую другую поляризацию по отношению к указанным, однако, ее можно представить в виде линейной комбинации упомянутых выше типов поляризации.

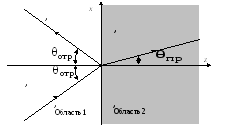
Рис.1.19. Падение плоской волны на границу раздела диэлектриков

Метод решения рассматриваемой задачи полностью аналогичен методу, примененному нами для решения задачи нормального падения волны на границу раздела сред: мы запишем выражения для падающей, отраженной и прошедшей волн в каждой области и используем граничные условия для определения неизвестных коэффициентов и углов.

Параллельная поляризация

В этом случае вектор электрического поля лежит в плоскости xz, и выражения для полей падающей плоской волны выглядят следующим образом

, (1.150а)

, (1.150б)

где и - волновое число и характеристическое сопротивление среды 1, соответственно. Отраженная и прошедшая волны описываются выражениями

, (1.151а)

, (1.151б)

, (1.152а)

. (1.152б)

В выражениях (1.151) и (1.152)  и T – коэффициенты отражения и передачи, и - волновое число и характеристическое сопротивление среды 2, соответственно. Таким образом, нам необходимо определить четыре неизвестных величины , T, и .

Согласно граничным условиям, необходимо выполнение равенства касательных составляющих и поля на границе раздела сред при z = 0. В связи с этим получим

, (1.153а)

. (1.153б)

Для того чтобы равенства (1.154) выполнялись для всех значений x на границе раздела, необходимо чтобы аргументы экспонент были одинаковы, т.е.

.

Последнее равенство, называемое иногда согласованием фаз, приводит нас к известному закону Снеллиуса для углов отражения и преломления

(1.154а)

(1.154б)

Используя соотношения (1.153) и (1.154), можно получить выражения для коэффициентов отражения и передачи

, (1.155а)

. (1.155б)

Заметим, что для нормального падения мы имеем , и формулы (1.155) переходят в соотношения (1.130). Кроме того, для рассматриваемой поляризации существует определенное значение угла падения , называемого углом Брюстера, при котором . В этом случае числитель (1.155а) обращается в ноль, т.е. и, учитывая

,

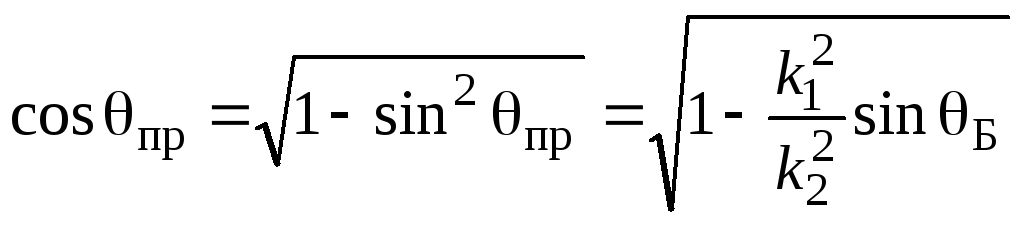получим . (1.156)