§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн

Пусть требуется найти поле в точке A, если сторонние источники заданы в некотором объеме V (B - текущая точка объема V). Задачи подобного типа, характерные для антенной техники, целесообразно решать в сферической системе координат (рис.1.8,а)

Для определения значений компонент поля в точке A необходимо, например, сначала решить уравнения (1.66) и (1.70) для компонент векторов Герца, а затем по (1.72) и (1.73) определить значения компонент поля.

Как мы установили уравнения (1.66) и (1.70) имеют наиболее простое решение в случае однородной безграничной среды с изотропными параметрами. Это решение для точки A имеет вид (1.67):

.

здесь , при этом в соответствии с рис.1.8,б выражается через радиус-векторы и , проведенные в точки A и B, и угол между ними:

(1.74)

Различают три зоны излучения.

1. Ближняя, или зона индукции. При расчете поля в этой зоне необходимо использовать точное выражение для .

2. Промежуточная, или зона френелевой дифракции. В этом случае существенно превышает . Формулу для можно преобразовать, применив разложение в ряд функции вида , где . Проведя разложение с учетом лишь членов до включительно, можно получить выражение для , соответствующее промежуточной зоне:

. (1.75)

3. Дальняя, или зона фраунгоферовой дифракции. Эта зона называется также волновой, и для нее справедливо соотношение . Вектор можно считать параллельным вектору . Модуль вектора определяется приближенной формулой

(1.76)

Деление на зоны связано с различным характером полей, присутствующих в каждой из зон. Так, в ближней зоне имеется относительно большое реактивное поле (связанное с источником) по сравнению с полем излучения. Если пренебречь полем излучения, то можно считать, что в ближней зоне среднее значение комплексного вектора Пойнтинга П равно нулю, и это соответствует колебательному движению энергии около источника.

В дальней зоне преобладает поле излучения, а реактивное поле пренебрежимо мало. Действительная компонента П направлена вдоль радиуса, определяющего направление излучения энергии.

Промежуточная зона является переходной от ближней зоны к дальней. В этой зоне поле излучения и реактивное поле соизмеримы.

Замена на в (1.67) дает выражение для электрического вектора Герца в дальней зоне:

(1.77)

где

(1.78)

Аналогичные соотношения в дальней зоне можно записать и для магнитного вектора Герца:

(1.79)

(1.80)

Введенные векторные функции и полностью определяются распределением источников, и характеризуют создаваемое источниками поле в дальней зоне излучения в зависимости от угловых координат и , поскольку

(1.81)

Штрих в формуле определяет угловые координаты источника, которые в общем случае могут занимать некоторый конечный объем V.

Рассмотрим пределы применимости приведенных выше соотношений. Фазовая ошибка, определяемая различием значений для промежуточной и дальней зон излучения, равна

(1.82)

Максимальное значение фазовой ошибки имеет место при Обозначив наибольший радиус области, занимаемой источниками, через , получим:

. (1.83)

Если принять, что (где - коэффициент, определяющий допустимую фазовую ошибку) можно получить условие дальней зоны:

, (1.84)

где D – наибольший размер излучающей системы.

На практике часто полагают , тогда условие дальней зоны принимает вид: . Это означает, что для удовлетворения условия дальней зоны приемная антенна должна находиться от передающей на расстоянии, не меньшем чем .

С учетом векторных функций и и того, что в дальней зоне отсутствуют сторонние токи (, функции и не зависят от координаты r, а радиальная составляющая оказывается обратно пропорциональной и существенно меньше поперечных компонент обратно пропорциональных r, из уравнения (1.73) получим выражения для полей в сферических координатах:

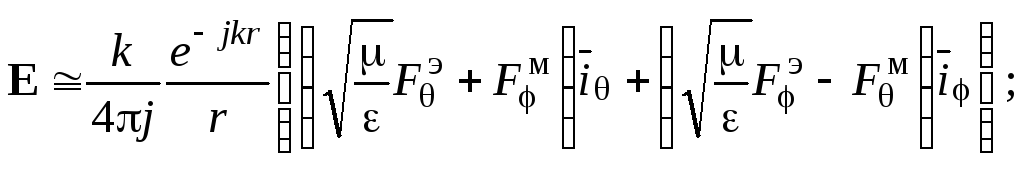(1.85)

(1.86)

Анализ формул (1.85) и (1.86) показывает, что поле в дальней зоне носит чисто поперечный характер, поскольку векторы E и H не имеют составляющих, направленных вдоль орта . В общем случае составляющие полей и сдвинуты по фазе, так что поле имеет эллиптическую поляризацию. Векторы E и H ортогональны, составляют с единичным вектором правую тройку векторов E, H, и связаны между собой множителем [Ом], который называется характеристическим сопротивлением среды и в общем случае является комплексной величиной, а для вакуума Ом.

Поле в дальней зоне подобно полю точечного источника, поскольку в соотношения (1.85) и (1.86) входит множитель . При этом в отличие от поля точечного источника поверхности равных фаз для каждой из составляющих векторов E и H не являются в общем случае сферами с центром в начале координат, поскольку составляющие и комплексны и зависят от угловых координат. В некоторых частных случаях удается найти фазовый центр, однако в общем случае излучающие системы фазового центра не имеют.