
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
§3.5. Двухпроводная линия передачи
Симметричная двухпроводная линия, как видно из рис. 3.14, состоит из двух параллельных проводников радиусом а, разнесенных на расстояние d между центрами проводников. Предполагается, что влияние предметов, окружающих линию, на структуру полей вблизи проводников пренебрежимо мало. Этот тип линии часто используется для соединения антенны, выполненной на симметричных вибраторах, с приемником. Чтобы выдержать требуемое расстояние d, в линии на рис.3.14 проводники закрепляют на тонких диэлектрических изоляторах.
Промышленностью выпускаются двухпроводные линии с волновым сопротивлением от 75 до 600 Ом. Для определения величины волнового сопротивления воспользуемся методикой, описанной в §2.2.
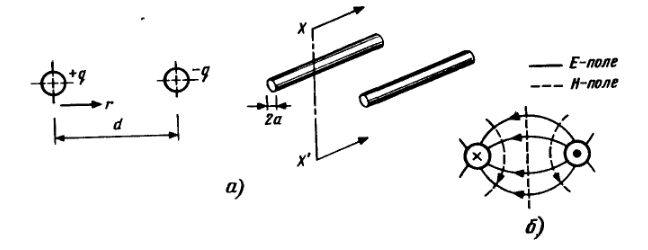
Рис.3.14. Поперечное сечение (а) и структура поля (б) в двухпроводной линии передачи
Начнем с определения погонной емкости, полагая, что величина заряда на каждом метре проводника одинакова и равна +q и –q - соответственно. Так как структура, изображенная на рис. 3.14, симметрична относительно плоскости Х – Х’, электрическая индукция в точке r, лежащей на прямой, соединяющей центры проводников, равна сумме индукций, создаваемых каждым из проводников:
![]() . (3.95)
. (3.95)
Разность потенциалов между проводниками вдвое превышает разность потенциалов между проводником и плоскостью Х - X'. Следовательно,
![]() . (3.96)
. (3.96)
Учитывая,
что
![]() ,
получим
,
получим
![]()
![]() . (3.97)
. (3.97)
При этом погонная емкость определится следующим выражением
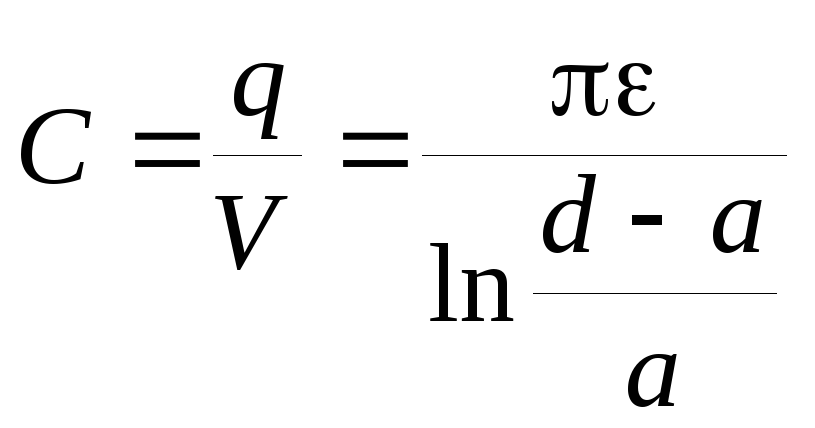 [Ф/м]. (3.98)
[Ф/м]. (3.98)
Перейдем к определению погонной индуктивности. Напряженность магнитного поля на расстоянии r от центра одиночного прямолинейного проводника бесконечной длины описывается по закону Ампера. Так как линия состоит из двух проводников, необходимо просуммировать поля от каждого из них
![]() . (3.98)
. (3.98)
Учитывая
соотношение
![]() ,
получим выражение для индукции магнитного
поля
,
получим выражение для индукции магнитного
поля
![]() . (3.99)
. (3.99)
Поток магнитной индукции, пронизывающий прямоугольник, одна из сторон которого параллельна радиусу r и равна dr, а вторая параллельна оси линии и равна единице, описывается выражением
![]() .
(3.100)
.
(3.100)
Полный
поток Ф, приходящийся на единицу длины
линии, равен интегралу
![]() .
Выполнив интегрирование, найдем погонную
индуктивность
.
Выполнив интегрирование, найдем погонную
индуктивность
![]() .
(3.101)
.
(3.101)
Откуда, можно определить характеристическое сопротивление среды
![]() .
(3.102)
.
(3.102)
§3.6. Коаксиальная линия передачи
Коаксиальная линия передачи - является линией закрытого типа, состоящей из двух соосно расположенных и изолированных друг от друга металлических проводников круглого сечения. В системах такого типа возможно существование волн TEM, E и H.
С овместим
ось z
цилиндрической системы координат r,
,
z
с осью внутреннего проводника коаксиальной
линии, ориентация других осей системы
изображена на рис.3.15.
овместим
ось z
цилиндрической системы координат r,
,
z
с осью внутреннего проводника коаксиальной
линии, ориентация других осей системы
изображена на рис.3.15.
Поперечные tem-волны
Рассмотрим
сначала низший тип волны в коаксиальной
линии, которым является TEM-волна,
поскольку у TEM-волны
![]() .
В этом случае
.
В этом случае
![]() ,
а потенциал U
удовлетворяет уравнению Лапласа:
,
а потенциал U
удовлетворяет уравнению Лапласа:
![]() .
Расписав лапласиан в цилиндрических
координатах, получим для U
уравнение вида
.
Расписав лапласиан в цилиндрических
координатах, получим для U
уравнение вида
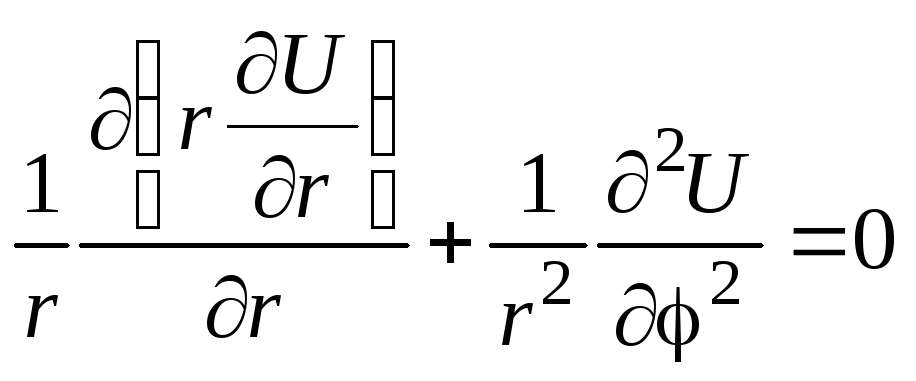 ,
(3.103)
,
(3.103)
которое может быть упрощено, поскольку система симметрична в азимутальном направлении и производная по обращается в нуль, т.е. имеем
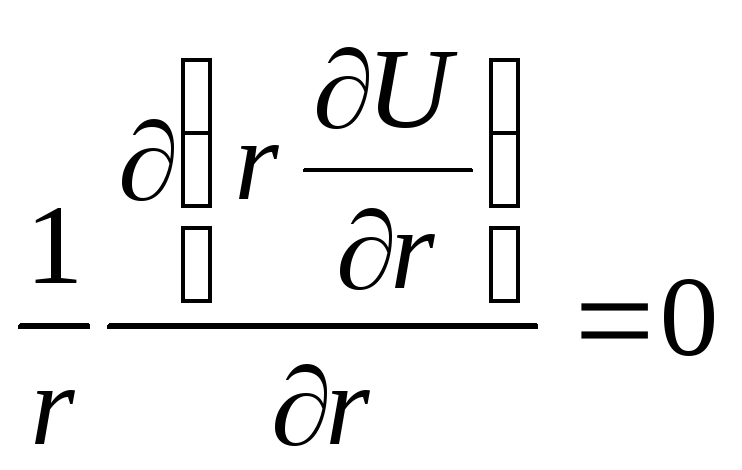 ,
(3.104)
,
(3.104)
откуда
![]() ,
,
![]() ,
,
![]() ,
,
![]() -
произвольные постоянные.
-
произвольные постоянные.
Определив U, находим функцию формы:
![]() .
(3.105)
.
(3.105)
Через функцию формы определяем все составляющие полей в коаксиальной линии в случае TEM-волны:
![]() ;
(3.106)
;
(3.106)
![]() ,
,
![]() ,
,
![]()
Структура поля TEM-волны в коаксиальной линии показана на рис.3.14.
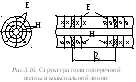
Найдем характеристическое сопротивление коаксиальной линии:
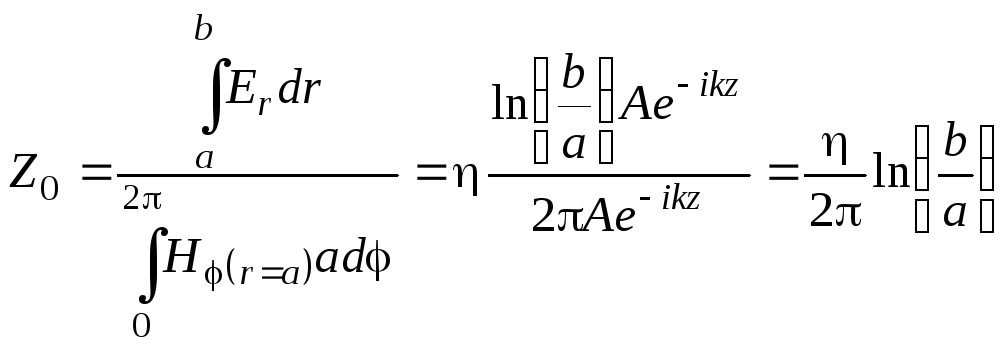 .
(3.107)
.
(3.107)
С учетом
того, что
![]() и
и
![]() ,
упростим формулу
для
,
упростим формулу
для
![]() :
:
![]() .
(3.108)
.
(3.108)
Предельная мощность, которая характеризует электрическую прочность коаксиальной линии, определяется электрическим полем у поверхности внутреннего проводника, так как оно на этой поверхности принимает максимальное значение:
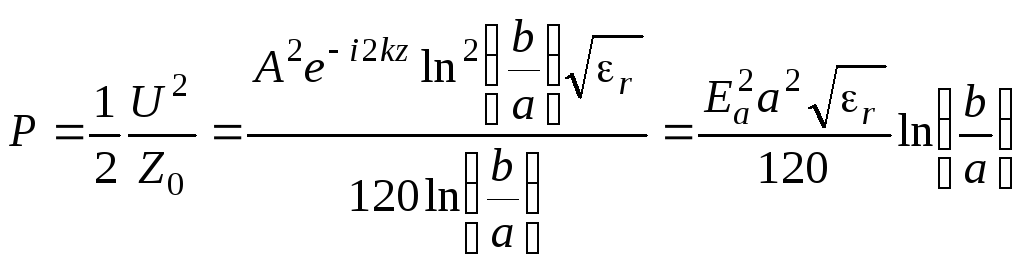 ,
(3.109)
,
(3.109)
здесь
![]() .
.
Приняв
во внимание, что для воздуха пробивная
напряженность электрического поля
составляет
![]() ,
и приравняв
,
и приравняв
![]() ,
можно найти предельную величину мощности,
передаваемой по коаксиальной линии с
воздушным заполнением. На практике
обычно пользуются понятием допустимой
мощности
,
можно найти предельную величину мощности,
передаваемой по коаксиальной линии с
воздушным заполнением. На практике
обычно пользуются понятием допустимой
мощности
![]() ,
где коэффициент
,
где коэффициент
![]() называется коэффициентом запаса.
называется коэффициентом запаса.
Постоянная затухания в коаксиальной линии, характеризующая потери в проводниках, определяется формулой
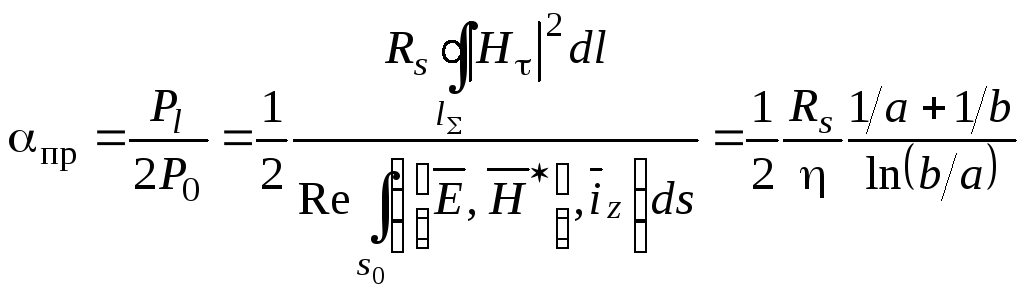 ,
(3.110)
,
(3.110)
где
![]() -
активная составляющая поверхностного
сопротивления проводника;
-
активная составляющая поверхностного
сопротивления проводника;
![]() - полный контур интегрирования (с учетом
всех металлических поверхностей);
- полный контур интегрирования (с учетом
всех металлических поверхностей);
![]() - площадь поперечного сечения линии без
сечения внутреннего проводника.
- площадь поперечного сечения линии без
сечения внутреннего проводника.
Потери в диэлектрике могут быть найдены по формуле (3.22б).
Анализ
формул (3.109) и (3.110) показывает, что если
зафиксировать внешний диаметр коаксиальной
линии, то максимум передаваемой мощности
имеет место при
![]() ,
а минимум потерь - при
,
а минимум потерь - при
![]() .
Поскольку
.
Поскольку
![]() соответствует
соответствует
![]() Ом,
а
Ом,
а
![]() отвечает
отвечает
![]() Ом,
то волновое сопротивление коаксиальной
линии в каждом случае выбирается с
учетом конкретных требований, обычно
выбирается
Ом,
то волновое сопротивление коаксиальной
линии в каждом случае выбирается с
учетом конкретных требований, обычно
выбирается
![]() или 75Ом.
или 75Ом.
