
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
§3.4. Круглый волновод
Полая металлическая труба круглого поперечного сечения также способна передавать волноводные волны E или H - типа. На рис.3.12 показано поперечное сечение круглого волновода с внутренним радиусом a.

Рис.3.12. Поперечное сечение круглого волновода
Поскольку мы имеем дело с цилиндрической геометрией, то решать уравнение (3.3) удобнее в цилиндрических координатах. При этом аналогично уравнениям (3.7) поперечные компоненты полей E или H - типа могут быть найдены через продольные:
![]() ,
(3.74а)
,
(3.74а)
![]() ,
(3.74б)
,
(3.74б)
![]() ,
(3.74в)
,
(3.74в)
![]() ,
(3.74г)
,
(3.74г)
где
![]() ,
,
![]() и предполагается существование только
прямой волны
и предполагается существование только
прямой волны
![]() .
В случае обратной волны необходимо
заменить
на - .
.
В случае обратной волны необходимо
заменить
на - .
Н-волны
Для волн
H
-
типа
![]() и уравнение (3.3) в цилиндрических
координатах принимает вид
и уравнение (3.3) в цилиндрических
координатах принимает вид
![]() . (3.75)
. (3.75)
Функция формы, являющаяся решением уравнения (3.75) имеет вид:
![]() .
(3.76)
.
(3.76)
Здесь
![]() и
и
![]() ,
функции Бесселя первого и второго рода.
Поскольку решение уравнения должно
быть периодично по ,
т.е.
,
функции Бесселя первого и второго рода.
Поскольку решение уравнения должно
быть периодично по ,
т.е.
![]() ,
то
,
то
![]() ,
должно быть целым числом, n.
Кроме этого, функция
,
должно быть целым числом, n.
Кроме этого, функция
![]() обращается в бесконечность при
обращается в бесконечность при
![]() ,
что физически невозможно, следовательно,
,
что физически невозможно, следовательно,
![]() .
Таким образом, решение уравнения для
.
Таким образом, решение уравнения для
![]() имеет вид
имеет вид
![]() ,
(3.76)
,
(3.76)
в котором
мы внесли постоянную C
в постоянные A
и B.
Определим теперь значение критического
волнового числа
![]() посредством
применения граничного условия
посредством
применения граничного условия
![]() на стенках волновода. Поскольку
на стенках волновода. Поскольку
![]() ,
то
,
то
![]() ,
при
,
при
![]() . (3.77)
. (3.77)
По
(3.74б) найдем
![]()
![]() , (3.78)
, (3.78)
здесь
![]() означает взятие производной по .
В результате для выполнения условия
означает взятие производной по .
В результате для выполнения условия
![]() при
при
![]() ,
необходимо
,
необходимо
![]() . (3.79)
. (3.79)
Если
определить решения уравнения
![]() как
как
![]() ,
то
,
то
![]() ,
можно найти в виде
,
можно найти в виде
![]() . (3.80)
. (3.80)
Значения
![]() приведены в математических таблицах,
первые несколько значений приведем в
таблице 3.1.
приведены в математических таблицах,
первые несколько значений приведем в
таблице 3.1.
Таблица
3.1.
Значения
![]() для
для
![]() - волн в круглом волноводе
- волн в круглом волноводе
|
n |
|
|
|
|
0 |
3.832 |
7.016 |
10.174 |
|
1 |
1.841 |
5.331 |
8.536 |
|
2 |
3.054 |
6.706 |
9.970 |
Таким
образом,
![]() волны, определяемые критическим волновым
числом
волны, определяемые критическим волновым
числом
![]() ,
в котором n
соответсвует вариациям по углу ,
а m - вариациям по радиусу .
Фазовая постоянная в этом случае
определяется соотношением
,
в котором n
соответсвует вариациям по углу ,
а m - вариациям по радиусу .
Фазовая постоянная в этом случае
определяется соотношением
 , (3.81)
, (3.81)
а частота отсечки
![]() . (3.82)
. (3.82)
Режиму
с наименьшей критической частотой
соответствует режим с минимальным
значением
![]() .
Из таблицы 3.1 находим, что таким режимом
будет
.
Из таблицы 3.1 находим, что таким режимом
будет
![]() ,
являющийся основным (рабочим) режимом
работы круголого волновода. Поскольку
,
являющийся основным (рабочим) режимом
работы круголого волновода. Поскольку
![]() ,
то отсутствует режим
,
то отсутствует режим
![]() ,
но присутсвуют колебания
,
но присутсвуют колебания
![]() .
.
Поперечные компоненты найдем по (3.74):
![]() ,
(3.83а)
,
(3.83а)
![]() ,
(3.83б)
,
(3.83б)
![]() ,
(3.83в)
,
(3.83в)
![]() .
(3.83г)
.
(3.83г)
В
полученных нами решениях присутствуют
две независимые постоянные A
и B.
В силу симметрии круглого волновода по
азимуту
![]() ,
оба решения
,
оба решения
![]() и
и
![]() допустимы и могут присутствовать при
любых углах. На практике, однако, значения
амплитуд слагаемых
допустимы и могут присутствовать при
любых углах. На практике, однако, значения
амплитуд слагаемых
![]() и
и
![]() зависят от способа возбуждения волновода
и могут быть обращены поочередно в ноль.
зависят от способа возбуждения волновода
и могут быть обращены поочередно в ноль.
Рассмотрим
теперь основное колебание
![]() ,
возбуждаемое таким образом, что
,
возбуждаемое таким образом, что
![]() .
Компоненты поля в этом случае имеют
вид:
.
Компоненты поля в этом случае имеют
вид:
![]() ,
(3.84а)
,
(3.84а)
![]() ,
(3.84б)
,
(3.84б)
![]() ,
(3.84в)
,
(3.84в)
![]() ,
(3.84г)
,
(3.84г)
![]() .
(3.84д)
.
(3.84д)
![]() .
(3.84е)
.
(3.84е)
Мощность, передаваемая по волноводу, может быть определена как
![]()
![]()

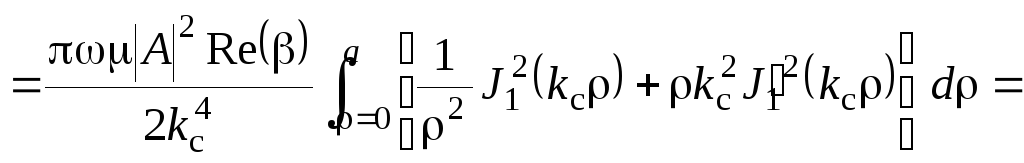
 ,
(3.85)
,
(3.85)
здесь использован табличный интеграл
 .
.
Значение мощности отлично от нуля только в случае, когда - действительная величина.
Затухание в диэлектрике, заполняющем волновод может быть найдено по (3.22а). Затухание вследствие потерь в проводнике определим, применяя метод возмущений:
![]()
![]()

 (3.86)
(3.86)
Применяя (3.85) и (3.86), получим выражение для постоянной затухания

 . (3.87)
. (3.87)
Е-волны
В случае
E-волн
решение для
![]() будет полностью аналогичным (3.76)
будет полностью аналогичным (3.76)
![]() .
(3.88)
.
(3.88)
Разница
между E
и H-типами
определяется граничными условиями: в
данном случае граничные условия
применяются непосредственно к
![]() ,
т.е.
,
т.е.
![]() ,
при
,
при
![]() . (3.89)
. (3.89)
Следовательно, имеет место уравнение
![]() , (3.90)
, (3.90)
или
![]() , (3.91)
, (3.91)
где
![]() - m-й
ноль функции
- m-й
ноль функции
![]() .
Значения
.
Значения
![]() приведены в математических таблицах,
первые несколько значений приведем в
таблице 3.2.
приведены в математических таблицах,
первые несколько значений приведем в
таблице 3.2.
Таблица
3.2.
Значения
![]() для
для
![]() - волн в круглом волноводе
- волн в круглом волноводе
|
n |
|
|
|
|
0 |
2.405 |
5.520 |
8.654 |
|
1 |
3.832 |
7.016 |
10.174 |
|
2 |
5.135 |
8.417 |
11.620 |
Фазовая постоянная в этом случае определяется соотношением
 , (3.92)
, (3.92)
а частота отсечки
![]() . (3.93)
. (3.93)
Режиму
с наименьшей критической частотой
соответствует режим с минимальным
значением
![]() .
Из таблицы 3.2 находим, что таким режимом
будет
.
Из таблицы 3.2 находим, что таким режимом
будет
![]() ,
однако, поскольку
,
однако, поскольку
![]() больше чем
больше чем
![]() ,
то данный режим не является основным
для круглого волновода. Поскольку
,
то данный режим не является основным
для круглого волновода. Поскольку
![]() ,
то отсутствует режим
,
то отсутствует режим
![]() .
.
Поперечные компоненты найдем по (3.74):
![]() ,
(3.94а)
,
(3.94а)
![]() ,
(3.94б)
,
(3.94б)
![]() ,
(3.94в)
,
(3.94в)
![]() .
(3.94г)
.
(3.94г)
Структуры полей некоторых режимов работы представлены на рис.3.13.

Рис.3.13. Структура полей в круглом волноводе
