§3.3. Прямоугольный волновод

В прямоугольном волноводе энергия распространяется внутри полой металлической трубы (рис.3.6) и существуют только волноводные волны H- и E-типов. Для определения составляющих полей необходимо найти функцию формы, удовлетворяющую волновому уравнению (3.3).

Н-волны

Рассмотрим широко используемые на практике H-волны . Для этого функцию формы  положим равной , а поперечные компоненты выразим через продольные с помощью уравнений (3.7). Функция формы, являющаяся решением волнового уравнения, имеет вид:

. (3.54)

На металлических поверхностях стенок волновода тангенциальные составляющие вектора E обращаются в нуль, поэтому граничные условия для прямоугольного волновода определяются соотношениями

Подставив функцию формы в соотношения для граничных условий, получим

откуда где

С учетом последних формул запишем в виде

, (3.55)

поскольку , а произвольная постоянная – произведение констант A и C из (3.54).

Поперечные компоненты выразим по (3.7)

; (3.56а)

; (3.56б)

; (3.56в)

. (3.56г)

Учитывая, что , находим выражение для критической длины волны любого типа колебаний (как H, так и E) в прямоугольном волноводе:

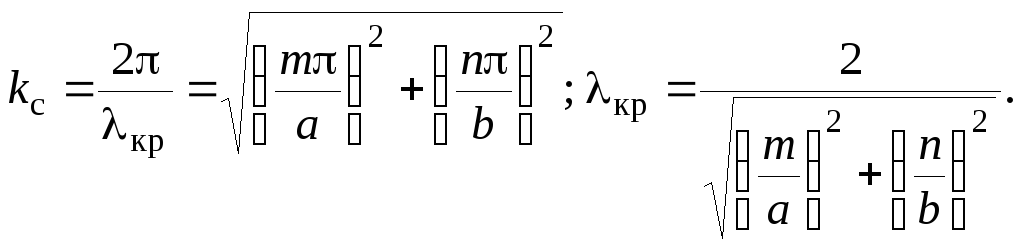(3.57)

Индексы m и n определяют число вариаций поля (число стоячих полуволн) соответственно вдоль широкой и узкой стенок волновода (обычно ).

Из формулы для видно, что каждому типу волны, отличающемуся индексами m и n, соответствует своя критическая длина волны. Однако при равных значениях m и n критические длины волн типов H и E совпадают. Типы колебаний, которые имеющие одинаковые критические частоты, но разные структуры полей, называются вырожденными.

Низшим типом волны в прямоугольном волноводе является волна , имеющая наибольшую критическую длину волны: . Волна представляет чрезвычайный практический интерес, поскольку она обеспечивает одноволновый режим работы волновода.

Выражая поперечные компоненты поля через , получаем следующие соотношения для составляющих поля волны (с точностью до постоянного множителя):

; (3.58а)

; (3.58б)

; (3.58в)

(3.58г)

Структура и эпюры электрического и магнитного полей в поперечном сечении прямоугольного волновода для волны типа представлены на рис.3.7 и 3.8. Из эпюр для магнитного поля видно, что существуют две продольные плоскости на расстоянии от узких стенок волновода (примерно на расстоянии ), где . В этих плоскостях имеет место круговая поляризация вектора H, что используется на практике при создании ферритовых устройств на базе прямоугольного волновода.

Каждой структуре поля в волноводе соответствует определенная система токов проводимости на его стенках. Вектор плотности поверхностного тока перпендикулярен вектору напряженности магнитного поля и аналитически выражается формулой , где - внутренняя нормаль (из металла).

Токи на широких стенках волновода определяются соотношениями:

(3.59а)

а на узких стенках:

. (3.59б)

На основании выражений для токов можно представить эпюры (рис.3.9) и картину распределения токов на стенках волновода для волны (рис.3.10). Из эпюр видно, что если прорезать продольную щель посредине широкой стенки волновода, то энергия не излучается, поскольку линии тока не прерываются щелью. Это свойство используется в волноводных измерительных линиях, в которых вдоль широкой стенки волновода перемещается измерительный зонд. Наоборот, если прорезать щель вдоль узкой стенки волновода, то энергия будет излучаться. Излучательные свойства щелей используются в щелевых антеннах.

Мощность, переносимая волной , определяется соотношением

. (3.60)

Заметим, что в данном случае результат отличен от нуля только когда  действительная величина и существует волноводный режим.

Затухание в волноводе определяется потерями в диэлектрике, заполняющем волновод, и в металле. Потери в диэлектрике можно учесть посредством формулы (3.22а).

Потери в проводнике определим с помощью метода возмущений:

, (3.61)

где поверхностное сопротивление стенок волновода, C периметр поперечного сечения волновода.

Подстановка значений для токов, с учетом их симметрии, из (3.59) в (3.61) приводит к следующему результату

. (3.62)

Следовательно, потери в проводниках для волны определяются как

(3.62)

Е-волны

Компоненты электромагнитного поля для E-волн определяются аналогичным образом. В этом случае функция формы  полагается равной и имеет такой же вид, что и для H-волн, а граничные условия определяются следующими выражениями:

Применив граничные условия, получим выражение для продольной компоненты электрического поля E-волн:

. (3.63)

Поперечные компоненты выражаются через также с помощью уравнений (3.7)

, (3.64а)

, (3.65б)

, (3.66в)

. (3.67г)

H_m0 - волны в волноводе, частично заполненном диэлектриком

Представленные выше результаты применимы для волноводов, полностью заполненных однородным диэлектриком, однако, во многих практически значимых задачах (таких как согласование сопротивлений или формирование требуемого сдвига фазы) применяются волноводы частично заполненные диэлектриком. В результате к уже применявшимся нами граничным условиям на поверхности металла необходимо добавить условия на границе раздела диэлектриков. Чтобы продемонстрировать подход к решению задач подобного рода рассмотрим распространение колебаний типа в волноводе, заполненном диэлектриком, как показано на рисунке 3.11.

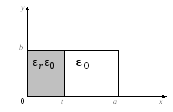
Рис.3.11. Поперечное сечение волновода, частично заполненного диэлектриком

Поскольку геометрия волновода однородна в направлении оси y и индекс , то моды не зависят от координаты y. Поэтому волновое уравнение (3.3) для может быть записано отдельно для диэлектрика и вакуума

, при , (3.68а)

, при , (3.68б)

где и критические волновые числа для диэлектрика и вакуума, определяемые следующим образом

, (3.69а)

, (3.69б)

Приведенные выражения означают, что фазовые постоянные в обеих частях волновода должны быть одинаковыми, поскольку необходимо выполнение условия согласования фаз на границе раздела сред при . В связи с этим решения выражений (3.67) получим в виде

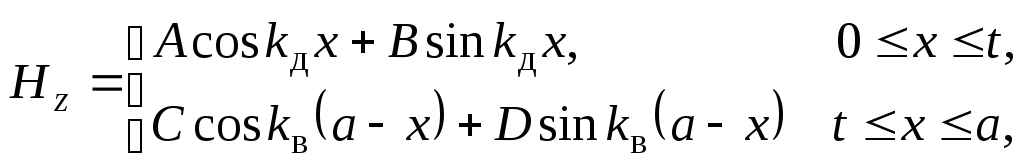(3.70)

решение для области выбрано с целью упростить применение граничных условий при .

Определим теперь и компоненты поля и применим граничные условия при . Для H - волн , а вследствие . определим из (3.7) и получим

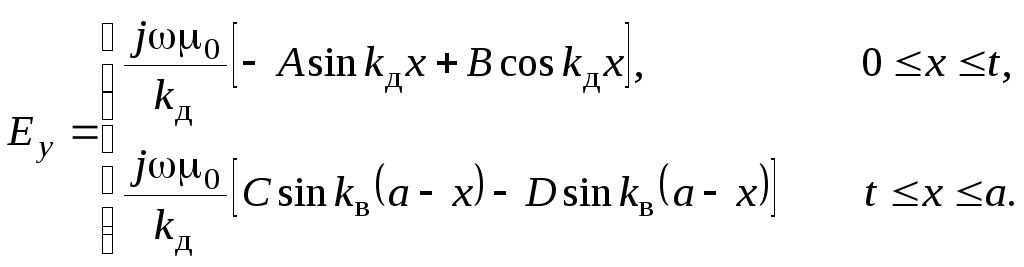(3.71)

При этом выполнение условия при требует обращения в ноль констант B и D. Далее при необходимо соблюсти условие непрерывности касательных составляющих . Из выражений (3.70) и (3.71) получим

, (3.72а)

. (3.72б)

Поскольку уравнения (3.72) однородные, то определитель матрицы коэффициентов системы должен обратиться в ноль, чтобы система имела не тривиальное решение. Следовательно,

, (3.73)

но поперечные волновые числа и выражаются через фазовую постоянную , и, значит, выражение (3.73) может быть решено относительно .

Решение (3.73) представляет собой бесконечное множество решений соответствующих модам .

Рассмотренный выше подход может быть применен ко множеству волноводов различной формы содержащих диэлектрические или магнитные неоднородности. Однако, в некоторых случаях оказывается невозможным удовлетворить граничным условиям только для одного вида колебаний E или H - типа и приходится использовать их комбинации.