Поперечные tem-волны

Поскольку у TEM-волны . В этом случае , и потенциал U(x,y) удовлетворяет уравнению Лапласа:

, для и . (3.23)

Поскольку начало отсчета потенциала может быть выбрано произвольно, предположим, что потенциал нижней пластины равен нулю (земля), а потенциал верхней пластины - , т.е. имеем

, (3.24а)

, (3.24б)

Так как поле вдоль оси x не меняется, то общее решение для (3.23) будет выглядеть следующим образом

, (3.25)

учитывая граничные условия (3.24), получим окончательно

. (3.26)

Таким образом, получим выражение для поперечной составляющей вектора E

, (3.27)

из которого следует уравнение для полного поля

, (3.28)

здесь - волновое число. В соответствии с уравнением (3.13) определим значение магнитного поля

. (3.29)

Заметим, что структура поля TEM-волн аналогична структуре поля плоской волны в бесконечной среде с параметрами  и .

Определим напряжение верхней пластины относительно нижней:

, (3.30)

как и ожидалось. Полный ток на верхней пластине может быть найден как из закона Ампера, так и с использованием выражения для поверхностной плотности тока:

. (3.31)

Используя выражения (3.30) и (3.31), определим характеристическое сопротивление TEM-волн

, (3.32)

которое является постоянной величиной и определяется геометрией линии передачи. Фазовая скорость, также является константой:

(3.33)

и равна скорости света в среде между пластинами.

Потери в диэлектрике могут быть определены по формуле (3.22б). Выражение для потерь же в проводниках определим в следующем пункте при рассмотрении E-волн.

Е-волны

Как было показано в параграфе 3.1 у E-волн , а , которая удовлетворяет уравнению (3.3), с учетом того, что получим

, (3.34)

здесь критическое волновое число. Общим решением уравнения (3.34) является выражение

. (3.35)

Для определения входящих в состав уравнения констант применим граничные условия

, при , (3.36)

откуда следует, что , а , для , или

, (3.37)

Таким образом, фазовая постоянная имеет следующий вид

, (3.38)

и мы имеем полное решение для

. (3.39)

Поперечные компоненты найдем, используя выражения (3.7)

, (3.40а)

, (3.40б)

. (3.40в)

Заметим, что для , , , а и постоянны вдоль оси y, т.е. волна типа является поперечной. Для каждого существует своя структура полей, обозначаемая и имеющая собственную постоянную распространения, задаваемую уравнением (3.38).

При этом согласно (3.16) критическая частота определяется как

. (3.41)

Самая низкая частота E-волн соответствует полю -, критическая частота поля вдвое больше и так далее.

Рассчитаем величину вектора Пойнтинга для определения направления передачи мощности. Согласно выражению (1.52) средняя за период мощность, проходящая через единичную площадку поперечного сечения двухпластинчатого волновода равна

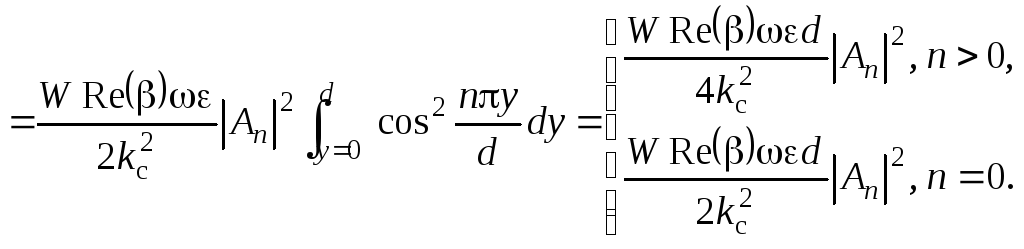(3.42)

Откуда следует, что положительна и отлична от нуля, когда  является действительной величиной, что выполняется при . В случае -  -чисто мнимая величина и .

Затухание, вызываемое потерями в диэлектрике, может быть определено по формуле (3.22а). Потери в проводниках определим, используя метод возмущений:

, (3.43)

где поток мощности, текущий через волновод в отсутствие потерь, согласно (3.42), а - потери мощности на единицу длины в двух проводниках с потерями, которые могут быть найдены по (1.149)

, (3.44)

здесь - поверхностное сопротивление проводников. Используя (3.42 – 3.44), получим выражение для потерь в проводниках

, для . (3.45)

Поскольку, как мы показали, TEM-волны эквивалентны волнам , то и для них справедливо полученное соотношение. Таким образом, для случая , получим из (3.43)

. (3.46)

Н-волны

В случае H-волн решение уравнения (3.34) имеет вид

. (3.47)

Граничные условия в данном случае: при . Откуда из (3.7) мы имеем

, (3.48)

постоянную и поперечное волновое число

, (3.49)

Окончательно для всех компонент поля получим

. (3.50)

, (3.51а)

, (3.51б)

. (3.51в)

Фазовые постоянные и критические частоты для H- и E-волн совпадают.

Мощность, переносимая по волноводу волной , может быть определена следующим образом

, для n > 0. (3.52)

Заметим, что при n = 0 - , поэтому , и отсутствует режим .

Легко показать (по аналоги с E-волнами), что затухание в проводниках определяется постоянной затухания

. (3.53)

Структура полей TEM, и в двухпластинчатом волноводе представлены на рис.3.5.

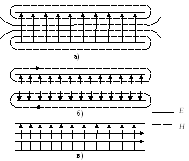
Рис.3.5. Структура полей TEM (а), (б) и (в) в двухпластинчатом волноводе