Волноводные волны h- и e-типов

Существование волноводных волн H(TE)- и E(TH)-типов определяется общим условием:

, . (3.14)

Если , то  - вещественная величина, следовательно, поле вдоль оси z экспоненциально затухает и не является волновым, так как перенос энергии вдоль z отсутствует. Такой режим работы волновода называется запредельным.

Если , то  - чисто мнимая величина. В этом случае имеет место передача энергии без затухания. Такой режим называется волновым и считается рабочим.

При - критический или предельный режим, тогда ,

. (3.15)

Таким образом, в отличие от поперечных волн, волноводные волны могут распространяться лишь начиная с критической длины волны или соответственно критической частоты

. (3.16)

Необходимо помнить, что, в отличие от частоты, критическая длина волны не зависит от свойств диэлектрика, заполняющего волновод.

Определим постоянную распространения:

,

где  - коэффициент затухания;  - фазовая постоянная.

Пусть , тогда

, (3.17)

(3.18)

где (или ) - длина волны в волноводе, а  - длина волны в неограниченной среде с параметрами  и .

Волновое сопротивление по полю для волноводов находится из отношения поперечных составляющих электрического и магнитного полей.

Для H-волны:

, (3.19а)

и для E-волны:

. (3.19б)

В данном случае волновое сопротивление оказывается частотнозависимой величиной. Волноводные волны H- и E-типов могут распространятся внутри полых металлических труб, а также в пространстве между двумя и более проводниками.

Влияние затухания в диэлектрике

Потери в линиях передачи могут возникать вследствие потерь в проводниках и диэлектриках. Если потери в диэлектриках определяются постоянной затухания , а потери в проводниках - , тогда общая постоянная затухания .

Затухание сигнала, вызванное потерями в проводниках, определяется с применением метода возмущений из параграфа 2.9. Указанные потери зависят от конфигурации поля в линии передачи и рассчитываются для каждого конкретного типа линии передачи. Расчет же потерь в диэлектрике для линий передачи, заполненных однородным диэлектриком, может быть произведен через постоянную распространения, а полученный результат применим для однородной линии передачи любого произвольного сечения.

Потери в диэлектрике учтем посредством комплексной диэлектрической проницаемости, в результате постоянную распространения запишем в виде

. (3.20)

Поскольку на практике применяют диэлектрики с весьма малыми потерями (), то уравнение (3.20) может быть заменено двумя первыми членами ряда Тейлора по :

, (3.21)

поскольку . В формуле (3.21) -действительная величина, что соответствует случаю отсутствия потерь. Выражение (3.21) показывает, что при малых потерях фазовая постоянная  остается неизменной, а постоянная затухания вследствие диэлектрических потерь определяется соотношением

(для H- и E-волн). (3.22а)

Аналогичный результат может быть получен и для TEM-волн, у которых и :

(для TEM-волн). (3.22б)

§3.3. Двухпластинчатый волновод

Двухпластинчатый волновод является одним из наиболее простых волноводов, в которых возможно существование волноводных волн H- и E-типов. Кроме того, в указанной линии передачи распространяются и поперечные волны, т.к. конструктивно данная линия состоит из двух проводников, как показано на рис.3.4.

Представление о двухпластинчатом волноводе позволяет наиболее простым способом изучать, например, явления возникновения высших типов колебаний в полосковых линиях передачи, а также исследовать поведение ускоряющих металлических линзовых антенн¹.

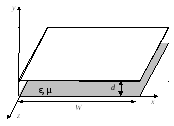
Рис.3.4. Двухпластинчатый волновод

Ширина пластин волновода W на рис.3.4 предполагается много большей расстояния между пластинами d, в связи с этим излучением с краев линии передачи и изменением поля вдоль оси x, пренебрегаем. При этом пространство между пластинами считаем заполненным диэлектриком с параметрами  и . Рассмотрим все типы колебаний.