
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
Уравнения Максвелла, приведенные в предыдущем параграфе, были записаны для вакуума. Однако на практике мы имеем дело с различными веществами и границами раздела тел, состоящих из разных веществ. С одной стороны, наличие среды усложняет уравнения электромагнитного поля, но с другой стороны позволяет использовать свойства этого вещества для создания устройств СВЧ с требуемыми качествами. При этом в веществе составляющие поля связаны между собой материальными уравнениями.
Например,
в диэлектриках внешнее электрическое
поле
![]() порождает поляризацию атомов и молекул
вещества, дипольные моменты которых
дополнительно изменяют индукцию
электрического поля
порождает поляризацию атомов и молекул
вещества, дипольные моменты которых
дополнительно изменяют индукцию
электрического поля
![]() .
Поляризационная составляющая вектора
электрической индукции называется
вектором
поляризованности
или просто поляризованностью
вещества и обозначается
.
Поляризационная составляющая вектора
электрической индукции называется
вектором
поляризованности
или просто поляризованностью
вещества и обозначается
![]() .
при этом материальное уравнение (1.2б)
приобретет следующий вид:
.
при этом материальное уравнение (1.2б)
приобретет следующий вид:
![]() . (1.15)
. (1.15)
Если рассматриваемая среда является линейной1, то поляризованность связана с напряженностью электрического поля линейным соотношением
![]() , (1.16)
, (1.16)
здесь
![]() -
электрическая восприимчивость среды,
в общем случае может быть комплексной
величиной. Тогда уравнение (1.15) может
быть записано как
-
электрическая восприимчивость среды,
в общем случае может быть комплексной
величиной. Тогда уравнение (1.15) может
быть записано как
![]() , (1.17)
, (1.17)
где ![]() (1.18)
(1.18)
есть комплексная диэлектрическая проницаемость среды. Мнимая часть определяет потери на нагрев среды, связанные с трением колеблющихся дипольных моментов (в вакууме, у которого действительная величина, потерь нет). Потери в диэлектрике могут быть представлены также в виде эквивалентных потерь проводимости, связанных с наличием отличной от нуля проводимости вещества . При этом в диэлектрике существует ток проводимости:
![]() . (1.19)
. (1.19)
Формула (1.19) выражает закон Ома с точки зрения теории электромагнитного поля. При этом второе уравнение Максвелла (1.14б) может быть записано в виде:
![]()
![]() . (1.20)
. (1.20)
Из
уравнения (1.20) видно, что потери на
переполяризацию
![]() неотделимы от потерь связанных с током
проводимости. Таким образом, выражение
неотделимы от потерь связанных с током
проводимости. Таким образом, выражение
![]() может рассматриваться как общая
эффективная
проводимость
среды. На практике для характеристики
СВЧ диэлектриков вводят понятие,
связанное с эффективной проводимостью,
называемое тангенсом
диэлектрических потерь:
может рассматриваться как общая
эффективная
проводимость
среды. На практике для характеристики
СВЧ диэлектриков вводят понятие,
связанное с эффективной проводимостью,
называемое тангенсом
диэлектрических потерь:
![]() , (1.21)
, (1.21)
который
характеризует соотношение действительной
и мнимой частей полного тока смещения.
СВЧ материалы обычно описываются
абсолютной диэлектрической проницаемостью,
являющейся действительной частью
комплексной диэлектрической проницаемости,
![]() (
(![]() - относительная диэлектрическая
проницаемость) и тангенсом потерь в
заданном частотном диапазоне. Здесь
стоит заметить, что если задача расчета
поля решена для случая среды без потерь,
то учесть потери можно, просто заменив
действительную диэлектрическую
постоянную на комплексную -
- относительная диэлектрическая
проницаемость) и тангенсом потерь в
заданном частотном диапазоне. Здесь
стоит заметить, что если задача расчета
поля решена для случая среды без потерь,
то учесть потери можно, просто заменив
действительную диэлектрическую
постоянную на комплексную -
![]() .
.
В
предшествовавших рассуждениях мы
предполагали, что
![]() совпадает
по направлению с вектором электрического
поля
совпадает
по направлению с вектором электрического
поля
![]() .
Материалы для которых выполняется
данное условие называются изотропными,
однако данное условие выполняется не
для всех материалов. В некоторых линейных
средах, называемых анизотропными,
связь между векторами поляризованности
и напряженности электрического поля
или между напряженностью и индукцией
электрического поля носит более сложный
характер и определяется в общем случае
тензором второго ранга:
.
Материалы для которых выполняется
данное условие называются изотропными,
однако данное условие выполняется не
для всех материалов. В некоторых линейных
средах, называемых анизотропными,
связь между векторами поляризованности
и напряженности электрического поля
или между напряженностью и индукцией
электрического поля носит более сложный
характер и определяется в общем случае
тензором второго ранга:
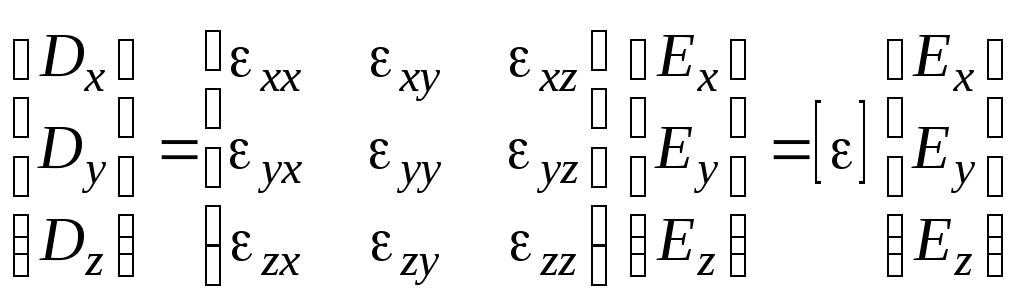 . (1.22)
. (1.22)
То есть
каждая из компонент напряженности
электрического поля влияет на все
компоненты вектора электрической
индукции. Примерами анизотропных веществ
являются некоторые кристаллы и
ионизированные газы. Для изотропных
материалов матрица
![]() станет диагональной со значениями
на главной диагонали.
станет диагональной со значениями
на главной диагонали.
Похожая
ситуация возникает и для магнетиков:
внешнее магнитное поле может повернуть
магнитные
дипольные моменты
вещества в определенном направлении,
т.е. произойдет магнитная
поляризация вещества
или намагничивание,
определяемое вектором
![]() .
При этом связь между напряженностью и
индукцией магнитного поля запишется
следующим образом
.
При этом связь между напряженностью и
индукцией магнитного поля запишется
следующим образом
![]() , (1.23)
, (1.23)
В случае
линейных магнитных материалов
![]() и
и
![]() связаны линейной зависимостью:
связаны линейной зависимостью:
![]() , (1.24)
, (1.24)
где
![]() - комплексная магнитная восприимчивость
вещества. С учетом (1.23) и (1.24) можно
получить выражение для линейных магнитных
сред:
- комплексная магнитная восприимчивость
вещества. С учетом (1.23) и (1.24) можно
получить выражение для линейных магнитных
сред:
![]() , (1.25)
, (1.25)
в котором
![]() есть комплексная магнитная проницаемость
среды, при этом мнимая часть
есть комплексная магнитная проницаемость
среды, при этом мнимая часть
![]() или
или
![]() описывает только потери трения,
возникающие при перемагничивании
вещества, поскольку магнитных токов и
зарядов в природе нет, то и потерь,
связанных с магнитной проводимостью
нет.
описывает только потери трения,
возникающие при перемагничивании
вещества, поскольку магнитных токов и
зарядов в природе нет, то и потерь,
связанных с магнитной проводимостью
нет.
Как и в случае с электрическим полем магнитные материалы также могут быть анизотропными и описываются тензором магнитной проницаемости вещества:
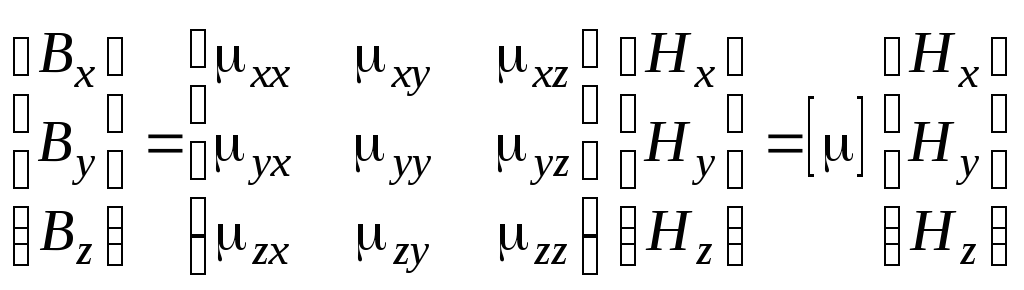 . (1.26)
. (1.26)
Одним из важнейших классов магнитных материалов, применяемых в СВЧ диапазоне частот, являются ферриты, на основе которых строятся многие СВЧ устройства, такие как фазовращатели, циркуляторы, поляризаторы и т.д.
Таким образом, в линейных средах система уравнений Максвелла для комплексных амплитуд принимает окончательный вид:
![]() ,
(1.27а)
,
(1.27а)
![]() ,
(1.27б)
,
(1.27б)
![]() ,
(1.27в)
,
(1.27в)
![]() .
(1.27г)
.
(1.27г)
Материальные уравнения же согласно (1.17) и (1.25) записываются как
![]() ,
(1.28а)
,
(1.28а)
![]() ,
(1.28б)
,
(1.28б)
при этом и , входящие в уравнения, могут быть как комплексными, так и тензорными величинами.
Заметим, что уравнения (1.27а и б) подчиняются принципу перестановочной двойственности, впервые сформулированному советским ученым А.А. Пистолькорсом в 1944г, и заключающимся в том, что замена в уравнении (1.27а)
![]() ,
,
![]() ,
,
![]() (1.29)
(1.29)
переводит его в уравнение (1.27б) и наоборот, а в целом система останется неизменной.
В общем случае уравнения Максвелла в дифференциальной форме (1.27а) – (1.27г) для свободных колебаний решаются в два этапа: на первом находятся решения в заданной области среды с неизвестными коэффициентами, а на втором определяются эти коэффициенты посредством наложения граничных условий электродинамики. Рассмотрим некоторые специальные виды граничных условий.
