
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
Биномиальный многосекционный трансформатор
Полоса
согласования биномиального трансформатора
является оптимальной в смысле минимального
отклонения величины коэффициента
отражения от значения на центральной
частоте внутри этой полосы. В связи с
этим характеристика указанного
трансформатора называется максимально
плоской.
Подобная максимально плоская характеристика
обеспечивается обращением в ноль первых
N
–
1 производных
![]() на центральной частоте
на центральной частоте
![]() .
Этим свойством обладает функция
следующего вида
.
Этим свойством обладает функция
следующего вида
![]() ,
(2.106)
,
(2.106)
для которой
![]()
![]() .
(2.107)
.
(2.107)
Здесь
![]() и
и
![]() для
для
![]() и
и
![]() (
(![]() соответствует центральной частоте
соответствует центральной частоте
![]() ,
для которой
,
для которой
![]() и
и
![]() ).
).
Определим
константу A
посредством предела
![]() .
Тогда
.
Тогда
![]() и (2.106) преобразуется к виду
и (2.106) преобразуется к виду
![]() ,
,
при
этом, поскольку
![]() ,
то все секции имеют нулевую электрическую
длину. Таким образом, постоянная A
может быть записана как
,
то все секции имеют нулевую электрическую
длину. Таким образом, постоянная A
может быть записана как
![]() .
(2.108)
.
(2.108)
С другой стороны в соответствии с формулой разложения бинома из (2.106) получим
![]() ,
(2.109)
,
(2.109)
здесь
![]() ,
(2.110)
,
(2.110)
коэффициенты
разложения бинома. Напомним, что
![]() ,
,
![]() и
и
![]() .
.
Приравняем требуемую характеристику коэффициента отражения из (2.109) и действительную характеристику отражения, приближенно описываемую выражением (2.103):
![]() .
.
Откуда
следует, что значение
![]() необходимо выбрать следующим образом
необходимо выбрать следующим образом
![]() ,
(2.111)
,
(2.111)
где A
задается посредством (2.108), а
![]() - биномиальный коэффициент.
- биномиальный коэффициент.
Характеристические
сопротивления секций могут быть найдены
из (2.102), однако, в силу малости частных
коэффициентов отражения
![]() справедлива следующая аппроксимация:
справедлива следующая аппроксимация:
![]() ,
,
т.к. для
малых x
-
![]() .
В результате с учетом (2.111) и (2.108) получим
выражение
.
В результате с учетом (2.111) и (2.108) получим
выражение
![]() ,
(2.112)
,
(2.112)
по
которому могут быть найдены все
![]() ,
начиная с n
= 0. При этом данный подход позволяет
легко провести проверку результатов
расчета – величина
,
начиная с n
= 0. При этом данный подход позволяет
легко провести проверку результатов
расчета – величина
![]() должна получиться равной
должна получиться равной
![]() .
.
Полоса
согласования биномиального трансформатора
может быть определена аналогично
односекционному четвертьволновому
трансформатору, посредством выбора
заданного уровня коэффициента отражения
![]() .
Тогда из (2.107) получим
.
Тогда из (2.107) получим
![]() ,
,
где
![]() нижняя граница полосы согласования
трансформатора (рис.2.24). Следовательно,
нижняя граница полосы согласования
трансформатора (рис.2.24). Следовательно,
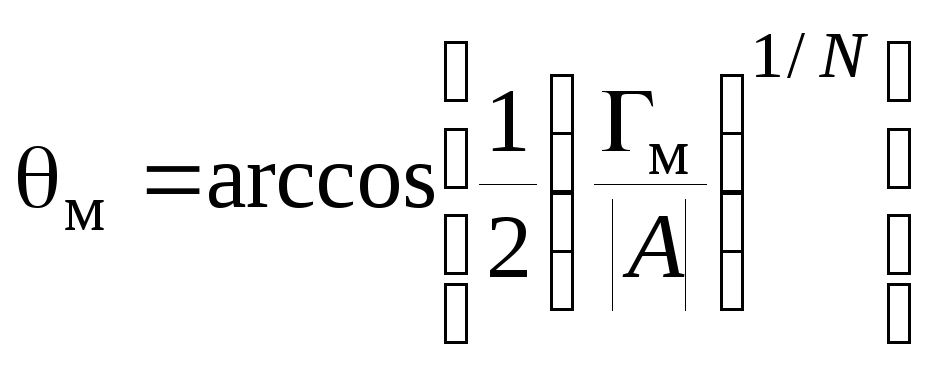 ,
(2.113)
,
(2.113)
и, применяя (2.92), найдем относительную полосу согласования
![]()
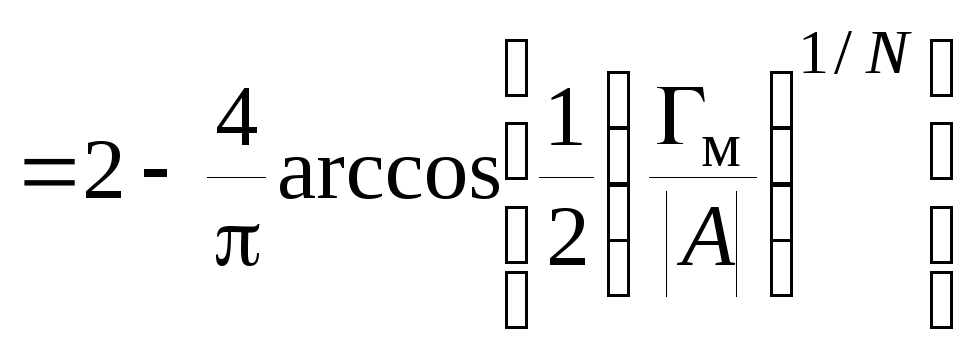 .
(2.114)
.
(2.114)
Сравнение
формул (2.92) и (2.114) показывает, что
относительная полоса согласования у
биномиального трансформатора шире чем
у односекционного в силу того, что
значение аргумента у функции
arccos в
(2.114) растет значительно медленнее при
увеличении разности между сопротивлением
нагрузки и характеристическим
сопротивлением входной линии передачи.
Графики зависимости модуля коэффициента
отражения от частоты для различного
числа секций, согласующих нагрузку
![]() и
линию с сопротивлением
и
линию с сопротивлением
![]() ,
представлены на рис. 2.28.
,
представлены на рис. 2.28.

Рис.2.28. Зависимость модуля коэффициента отражения от частоты для биномиальных трансформаторов при разном количестве секций N
Многосекционный трансформатор Чебышева
В отличии
от биномиального согласующего
трансформатора, трансформатор Чебышева
осуществляет согласование при наличии
колебаний модуля коэффициента отражения
в полосе согласования. Однако, для любого
заданного максимального значения
коэффициента отражения в полосе
трансформатор Чебышева имеет более
широкую полосу согласования, по сравнению
с биномиальным при заданном количестве
секций. Трансформатор Чебышева строится
посредством представления функции
коэффициента отражения
![]() полиномами Чебышева. Рассмотрим вначале
свойства полиномов Чебышева.
полиномами Чебышева. Рассмотрим вначале
свойства полиномов Чебышева.
Полином
Чебышева первого рода n
- го порядка обозначается
![]() .
Приведем первые четыре полинома Чебышева
.
Приведем первые четыре полинома Чебышева
![]() ,
(2.115а)
,
(2.115а)
![]() ,
(2.115б)
,
(2.115б)
![]() ,
(2.115в)
,
(2.115в)
![]() .
(2.115г)
.
(2.115г)
При этом полиномы более высоких порядков могут быть представлены рекуррентной формулой
![]() .
(2.116)
.
(2.116)
На рис.2.29 приведены первые четыре полинома Чебышева. Данный рисунок позволяет определить некоторые очень полезные свойства полиномов Чебышева:
- для
![]() ,
,
![]() ;
в этом диапазоне полиномы Чебышева
колеблются между
;
в этом диапазоне полиномы Чебышева
колеблются между
![]() ;
данный диапазон можно выбрать в качестве
полосы согласования;
;
данный диапазон можно выбрать в качестве
полосы согласования;
- для
![]() ,
,
![]() ;
в данном диапазоне получим значения
коэффициента отражения вне полосы
согласования;
;
в данном диапазоне получим значения
коэффициента отражения вне полосы
согласования;
- для
![]() ,
,
![]() растет с увеличением x
тем быстрее, чем больше n.
растет с увеличением x
тем быстрее, чем больше n.

Рис.2.29. Первые четыре полинома Чебышева
Пусть
![]() при
при
![]() ,
тогда полиномы могут быть представлены
в виде
,
тогда полиномы могут быть представлены
в виде
![]() ,
,
или в более общем виде
![]() ,
при
,
при
![]() ,
(2.117а)
,
(2.117а)
![]() ,
при
,
при
![]() .
(2.117б)
.
(2.117б)
При
проектировании трансформатора желательно,
чтобы колебания коэффициента отражения
внутри полосы согласования были
одинаковыми, для этого необходимо
сопоставить значению
![]() величину
величину
![]() ,
а
,
а
![]() -
-
![]() (см. рис.2.24). Последнее условие выполняется
путем замены в (2.117)
(см. рис.2.24). Последнее условие выполняется
путем замены в (2.117)
![]() на
на
![]() :
:
 .
(2.118)
.
(2.118)
Так как
![]() при
при
![]() ,
то
,
то
![]() для данного диапазона значений .
для данного диапазона значений .
Применяя
формулы понижения степени, приводящие
![]() к виду
к виду
![]() ,
запишем полиномы Чебышева в форме
удобной для проектирования согласующего
трансформатора:
,
запишем полиномы Чебышева в форме
удобной для проектирования согласующего
трансформатора:
![]() ,
(2.119а)
,
(2.119а)
![]() ,
(2.119б)
,
(2.119б)
![]() ,(2.119в)
,(2.119в)
![]()
![]() .
(2.119г)
.
(2.119г)
Далее обратимся вновь к разложению коэффициента отражения в ряд по частным коэффициентам (2.105), и помня о том, что мы проектируем трансформатор с Чебышевской характеристикой, составим следующее равенство
![]()
![]() ,
(2.120)
,
(2.120)
здесь
последний член в разложении равен
![]() для четного N
и
для четного N
и
![]() для нечетного. Как и в случае биномиального
трансформатора мы можем найти константу
A
посредством устремления
для нечетного. Как и в случае биномиального
трансформатора мы можем найти константу
A
посредством устремления
![]() .
Поскольку
.
Поскольку
![]() ,
,
то
имеем ![]() .
(2.121)
.
(2.121)
При этом
в связи с тем, что максимальное значение
модуля коэффициента отражения в полосе
согласования равно
![]() ,
то из (2.120) имеем равенство
,
то из (2.120) имеем равенство
![]() ,
так как величина
,
так как величина
![]() в полосе согласования не превышает
единицы. Тогда из (2.121) можем записать
в полосе согласования не превышает
единицы. Тогда из (2.121) можем записать
![]() ,
,
и, применяя (2.117б), получим

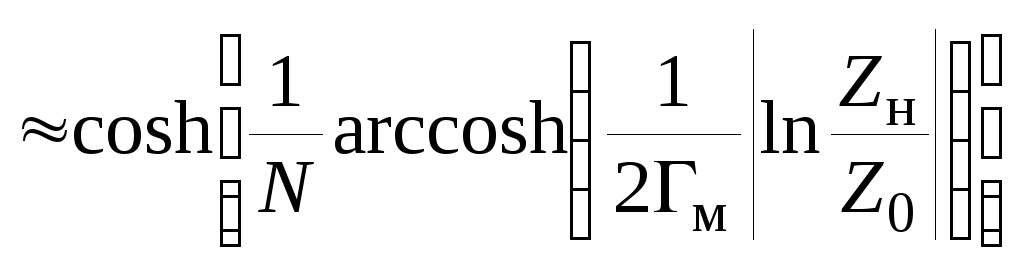 .
(2.122)
.
(2.122)
Определив
с помощью (2.122) величину
![]() ,
можно найти относительную полосу
согласования трансформатора по формуле
(2.92)
,
можно найти относительную полосу
согласования трансформатора по формуле
(2.92)
![]() .
(2.123)
.
(2.123)
Частные
коэффициенты отражения секций
![]() могут быть найдены по (2.120) путем раскрытия
полинома Чебышева соответствующего
порядка и приравнивания коэффициентов
при членах вида
могут быть найдены по (2.120) путем раскрытия
полинома Чебышева соответствующего
порядка и приравнивания коэффициентов
при членах вида
![]() .
По
.
По
![]() можно с помощью формул (2.102) определить
значения характеристических сопротивлений
можно с помощью формул (2.102) определить
значения характеристических сопротивлений
![]() секций. Однако, подход, примененный нами
при расчете сопротивлений биномиального
трансформатора, позволяет упростить
количество вычислений и осуществить
самопроверку результата и в случае
трансформатора Чебышева. Согласно
указанному подходу
секций. Однако, подход, примененный нами
при расчете сопротивлений биномиального
трансформатора, позволяет упростить
количество вычислений и осуществить
самопроверку результата и в случае
трансформатора Чебышева. Согласно
указанному подходу
![]() .
.
Графики
зависимости модуля коэффициента
отражения от частоты для различного
числа секций Чебышевского трансформатора,
согласующих нагрузку
![]() и
линию с сопротивлением
и
линию с сопротивлением
![]() ,
представлены на рис. 2.30.
,
представлены на рис. 2.30.

Рис.2.30. Зависимость модуля коэффициента отражения от частоты для трансформаторов Чебышева при разном количестве секций N
