§2.7. Четвертьволновый трансформатор сопротивлений
Применение рассмотренного выше согласования с помощью сосредоточенных элементов схемы ограничено соотношением между размерами реальных элементов и длиной волны в линии передачи. В настоящее время существующие чип компоненты (тип корпусов 0402) позволяют создавать схемы согласования на частотах до 5 – 6ГГц. В более высоком диапазоне частот применяются способы согласования, основанные на свойстве длинных линий преобразовывать сопротивление нагрузки вдоль линии передачи.
Простейшей
схемой согласования является
четвертьволновый
трансформатор,
представляющий собой отрезок линии
передачи длиной
.
Согласно (2.54)
. (2.81)
Если
сопротивление нагрузки чисто активное
или в качестве нагрузки выступает линия
с другим характеристическим сопротивлением
,
то входное сопротивление линии длиной
также является чисто активным. Это
свойство может быть использовано для
согласования двух линий передачи с
разными волновыми сопротивлениями
(рис.2.22, а), а также линии с произвольной
активной нагрузкой (рис.2.22, б).
Рис.2.22. Согласование посредством четвертьволнового трансформатора двух линий передачи с разными характеристическими сопротивлениями (а), и линии передачи с произвольной активной нагрузкой (б)
При этом для схем, представленных на рис. 2.22 легко получить условия согласования:
, (2.82)
, (2.83)
здесь
- характеристическое сопротивление
трансформатора.
С помощью четвертьволнового трансформатора можно согласовать и комплексную нагрузку. Для этого трансформатор надо включить на таком расстоянии от нагрузки, где ее входное сопротивление является чисто активным (точки А и Б на рис. 2.23).
Рис.2.23. Согласование комплексной нагрузки четвертьволновым трансформатором
Из рис.2.23 следует
(2.84)
В этом случае условия согласования имеют вид:
и
. (2.85)
Очевидно,
что идеальное согласование сопротивлений
выполняется только на рабочей частоте
,
т.е. только при условии
.
Рассмотрим теперь подробнее поведение
трансформатора в некоторой полосе
частот вблизи рабочей частоты. Такое
рассмотрение необходимо, поскольку для
передачи информации всегда, по
определенному закону, изменяется какая
либо характеристика сигнала (амплитуда,
частота или фаза), что приводит к появлению
целого спектра частот вблизи рабочей
частоты, имеющего определенную ширину
.
Подробное введение в теорию радиосигналов
можно найти в [10].
Введем
обозначение
и,
учитывая (2.81), запишем выражение для
коэффициента отражения во входном
сечении четвертьволнового трансформатора
. (2.86)
Поскольку
,
получим
. (2.87)
При этом модуль коэффициента отражения имеет следующий вид
,
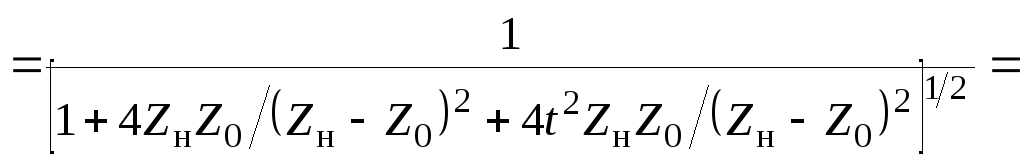
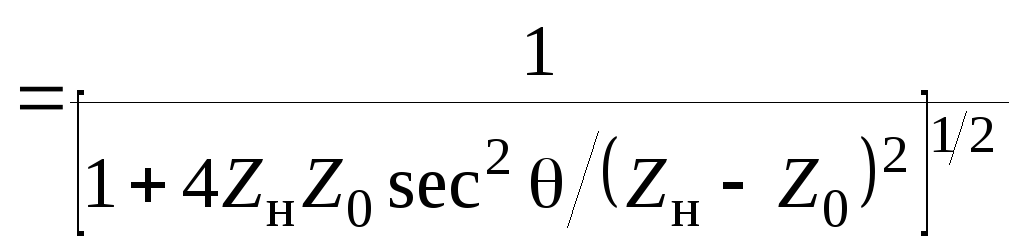(2.88)
здесь
учтено
.
Теперь
учтем наше предположение о близости
рассматриваемых частот к рабочей частоте
.
В этом случае
,
,
и (2.88) можно записать в виде
. (2.89)
Формула (2.89) дает приблизительную оценку полосы согласования в окрестности рабочей частоты, примерный вид кривой модуля коэффициента отражения показан на рис.2.24.
Рис.2.24. Поведение модуля коэффициента отражения четвертьволнового трансформатора вблизи рабочей частоты
Если
задать максимально допустимое значение
модуля коэффициента отражения
,
то можно определить полосу
согласования
трансформатора
, (2.90)
учитывая
симметрию (2.88) относительно
и
при
и при
.
Приравнивая
соответствующему значению из (2.88),
определим выражение для
:
,
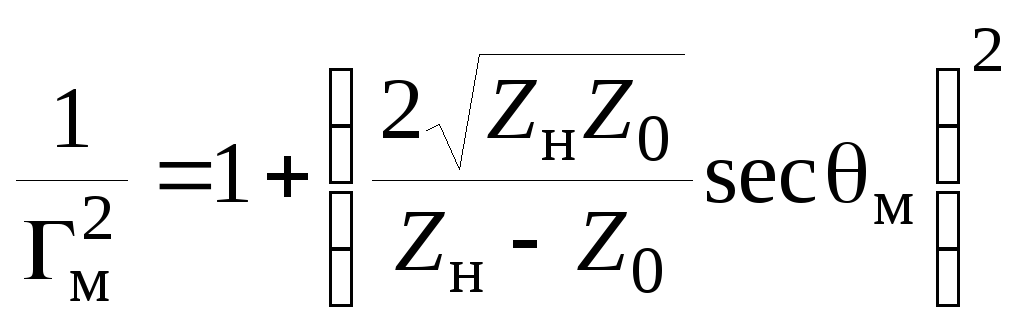или
. (2.91)
Рассчитаем диапазон частот согласования для линий передачи с поперечными TEM волнами, в которых справедливы следующие соотношения
,
откуда
следует значение нижней частоты полосы
согласования при
.
Из последнего выражения может быть найдена относительная полоса согласования трансформатора
. (2.92)
Обычно
относительная полоса частот выражается
в процентах,
.
Из (2.92)
следует, что полоса согласования
увеличивается с приближением значения
к значению
.
Полученные результаты строго справедливы только для линий с TEM-волнами. В линиях с другими типами волн (таких как волноводы) постоянная распространения не является линейной функцией частоты, а волновое сопротивление становится частотно зависимым. Эти факторы усложняют результат расчета коэффициента отражения четвертьволнового трансформатора в таких линиях передачи, однако, полоса пропускания трансформатора обычно достаточно мала и указанные сложности не сильно влияют на результат. Кроме того, другим фактором, который мы игнорировали в приведенном выше анализе, являются паразитные емкости, связанные со скачками характеристических сопротивлений на стыках линий передачи. Подобные неоднородности могут быть компенсированы путем введения небольших изменений в длину четвертьволнового трансформатора.
На рис.2.25 показан ряд зависимостей модуля коэффициента отражения от относительной частоты отстройки для разных соотношений сопротивлений линии и нагрузки.
Рис.2.25. Модуль коэффициента отражения четвертьволнового трансформатора для различного соотношения согласуемых нагрузок