
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
§2.6. Согласование посредством сосредоточенных параметров
На относительно низких частотах от единиц мегагерц до нескольких гигагерц для согласования можно применять цепи на сосредоточенных элементах. Согласующие цепи на сосредоточенных элементах могут состоять из реактивных, резистивных элементов либо из их сочетания.
Если согласующая цепь состоит из резистивных элементов, то согласование достигается посредством рассеивания части мощности поступающей в нагрузку. Этому уменьшению мощности соответствует определенное затухание, вносимое аттенюатором.
Рассмотрим самый простой аттенюатор, представляющий собой Г-образную резистивную цепь.
Г-образная резистивная согласующая цепь
Эта цепь состоит из двух резисторов и является простейшей согласующей секцией (рис. 2.17).
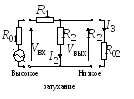
Рис.2.17. Г-образная согласующая цепь из активных сопротивлений
Она
используется для согласования
характеристических сопротивлений
![]() и
и
![]() .
Условие для согласования по входу
.
Условие для согласования по входу
![]()
Для согласования по выходу
![]() .
.
Следовательно,
![]() ,
(2.58а)
,
(2.58а)
![]() .
(2.58б)
.
(2.58б)
Складывая, получаем
![]() (2.59)
(2.59)
Поочередно
выражая из (2.59)
![]() и
и
![]() ,
и подставляя результат в (2.58 а и б),
получим выражения для
,
и подставляя результат в (2.58 а и б),
получим выражения для
![]() и
и
![]()
![]() ,
(2.60а)
,
(2.60а)
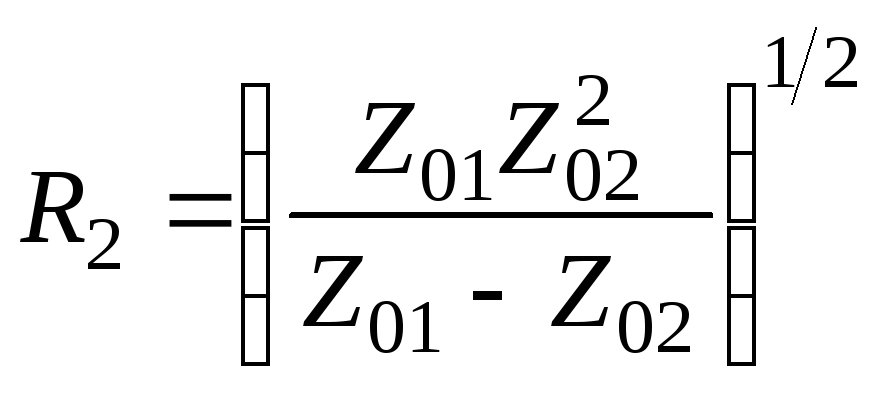 .
(2.60б)
.
(2.60б)
Если
цепь выполнена в соответствии с последними
равенствами, то падающая волна проходит
без отражений, когда согласующая цепь
включена между двумя разными волновыми
сопротивлениями. Затухание, вносимое
этой цепью, вычисляется по известным
величинам токов. Обозначив падение
напряжения на входе цепи через
![]() ,
из уравнений Кирхгофа находим
,
из уравнений Кирхгофа находим
![]() ,
,
![]() .
.
Следовательно, затухание L вносимое согласующим аттенюатором
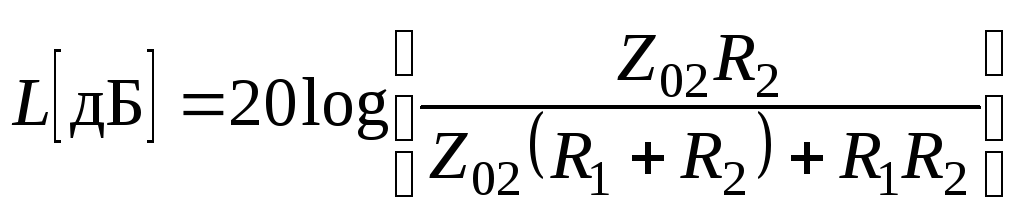 . (2.61)
. (2.61)
Согласующие цепи на реактивных элементах
Рассмотрим
согласующие Г-, Т- и П-образные цепи на
сосредоточенных реактивных элементах
и построение основано на следующем
принципе: произвольную последовательную
цепь, состоящую из последовательно
включенных активного
![]() и реактивного
и реактивного
![]() сопротивлений, можно заменить эквивалентной
цепью, состоящей из параллельно включенных
активного
сопротивлений, можно заменить эквивалентной
цепью, состоящей из параллельно включенных
активного
![]() и реактивного
и реактивного
![]() сопротивлений (рис. 2.18).
сопротивлений (рис. 2.18).

Рис.2.18. Последовательная и параллельная LR-цепи
Для
последовательной цепи
![]() ,
т.е.
,
т.е.
![]() . (2.62)
. (2.62)
Для
параллельной цепи
![]() ,
следовательно,
,
следовательно,
![]() . (2.63)
. (2.63)
Приравниваем (2.62) и (2.63):
![]() . (2.64)
. (2.64)
С целью упрощенной записи введем понятие добротности для цепей, изображенных на рис. 2.18:
![]() (энергия,
запасенная в цепи/энергия, рассеиваемая
в цепи за 1с).
(энергия,
запасенная в цепи/энергия, рассеиваемая
в цепи за 1с).
Для последовательной цепи LR (рис. 2.18)
![]() . (2.65)
. (2.65)
Для параллельной цепи LR
![]() . (2.66)
. (2.66)
Подставляя (2.65) и (2.66) в (2.64), получаем
![]() . (2.67)
. (2.67)
Из (2.67)
следует, что два произвольных активных
сопротивления
![]() и
и
![]() могут быть согласованы, если обеспечить
требуемую добротность согласующей
цепи. Вид согласующих Г-образных LC
–
цепей представлен на рис. 2.19.
могут быть согласованы, если обеспечить
требуемую добротность согласующей
цепи. Вид согласующих Г-образных LC
–
цепей представлен на рис. 2.19.
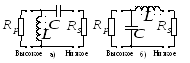
Рис.2.19. Г-образная согласующая цепь
Выбор конкретной схемы (рис. 2.19, а или б) зависит от возможности реализации рассчитанных величин элементов.
В согласующих LC-цепях добротность Q зависит только от отношения входного и выходного сопротивлений, что является их недостатком, поскольку с помощью таких цепей можно согласовывать сопротивления, величины которых заметно отличаются друг от друга. Целесообразно выбирать добротность цепи в пределах 10 … 20. При более низких Q слабо подавляются гармоники входного сигнала. Слишком высокая добротность приводит к увеличению потерь в цепи из-за больших токов в резонансе. В случае, если требуются слишком высокие Q, т.е. перепад согласуемых сопротивлений велик, используют каскадное соединение двух и более секций с более низкими значениями Q.
Применение
Т-образной схемы позволяет устранить
некоторые недостатки Г-звена. На рис.
2.20 показана такая согласующая Т-образная
цепь из реактивных элементов, которую
можно представить состоящей из двух
Г-звеньев, нагруженных на эквивалентное
активное сопротивление
![]() (рис. 2.20, б). Такое представление удобно,
поскольку позволяет для расчета
использовать свойства Г-звена. Величина
(рис. 2.20, б). Такое представление удобно,
поскольку позволяет для расчета
использовать свойства Г-звена. Величина
![]() должна быть больше каждой из величин
согласуемых сопротивлений
должна быть больше каждой из величин
согласуемых сопротивлений
![]() и
и
![]() ,
так как согласно (2.67)
,
так как согласно (2.67)
![]() .
Реактивное сопротивление
.
Реактивное сопротивление
![]() образуется параллельным соединением
образуется параллельным соединением
![]() и
и
![]() .
При расчете схемы предполагается, что
известны
.
При расчете схемы предполагается, что
известны
![]() ,
,
![]() и добротность Q1.
и добротность Q1.

Рис.2.20. Т-образная согласующая цепь: а) эквивалентная схема; б) разбиение на Г-образные секции; в) пример конкретной реализации
Для первого Г-звена (рис. 2.19, б) из (2.67) находим
![]() . (2.68)
. (2.68)
Если
рассчитанная по (2.68) величина
![]() окажется меньше
окажется меньше
![]() или
или
![]() ,
то следует увеличить
,
то следует увеличить
![]() и вычислить новое значение
и вычислить новое значение
![]() .
Из (2.65) и (2.66) определяем
.
Из (2.65) и (2.66) определяем
![]() , (2.69)
, (2.69)
![]() . (2.70)
. (2.70)
Для
второго Г-звена (2.19, б) из (2.67) находим
![]() .
Поэтому
.
Поэтому
![]() . (2.71)
. (2.71)
С помощью (2.71) из (2.65) и (2.66) определяем
![]() , (2.72)
, (2.72)
![]() . (2.73)
. (2.73)
Таким образом, для Т-образной цепи (2.20, а)
![]() . (2.74)
. (2.74)
Перейдем
к рассмотрению согласующих П-образных
цепей из реактивных элементов (рис.
2.21, а). Для анализа такой цепи, как и
ранее, представим ее в виде двух Г-звеньев,
нагруженных на активное сопротивление
![]() (рис. 2.21, б). Величина
(рис. 2.21, б). Величина
![]() должна быть меньше каждой из величин
согласуемых сопротивлений
должна быть меньше каждой из величин
согласуемых сопротивлений
![]() и
и
![]() ,
так как согласно (2.67)
,
так как согласно (2.67)
![]() ,
а реактивное сопротивление
,
а реактивное сопротивление
![]() образуется последовательным соединением
образуется последовательным соединением
![]() и
и
![]() .
.
Для
первого Г-звена (рис.2.21, б) по известным
![]() и
и
![]() и заданной добротности
и заданной добротности
![]() из (2.67) находим
из (2.67) находим
![]() .
(2.75)
.
(2.75)
Если
![]() ,
рассчитанное из (2.75), будет больше
,
рассчитанное из (2.75), будет больше
![]() или
или
![]() ,
то необходимо увеличить
,
то необходимо увеличить
![]() и вычислить новое значение
и вычислить новое значение
![]() .
Из (2.65) и (2.66) определяем
.
Из (2.65) и (2.66) определяем
![]() , (2.75)
, (2.75)
![]() . (2.76)
. (2.76)
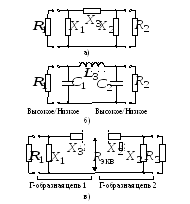
Рис.2.21. П-образная согласующая цепь: а) эквивалентная схема; б) разбиение на Г-образные секции; в) пример конкретной реализации
Для второго Г-звена из (2.67) следует
![]() (2.77)
(2.77)
С помощью (2.77) из (2.65) и (2.66) находим
![]() , (2.78)
, (2.78)
![]() . (2.79)
. (2.79)
Определяем
![]() для П-образной цепи
для П-образной цепи
![]() . (2.80)
. (2.80)
В случае
наличия реактивной составляющей у
сопротивлений источника и нагрузки,
необходимо вести расчет аналогично,
используя в качестве
![]() и
и
![]() активные составляющие согласуемых
сопротивлений, а на этапе расчета
параметров схемы (значений индуктивностей
и емкостей) учесть реактивные составляющие,
добавляя или вычитая их значения из
активные составляющие согласуемых
сопротивлений, а на этапе расчета
параметров схемы (значений индуктивностей
и емкостей) учесть реактивные составляющие,
добавляя или вычитая их значения из
![]() и
и
![]() .
.
