
- •К.С.Лялин, д.В.Приходько Электродинамика свч
- •Введение
- •Часть I. Теория электромагнитного поля.
- •§1.1. Уравнения Максвелла, как метод описания электромагнитного поля в однородных средах.
- •§1.2. Электромагнитные поля в различных средах и граничные условия электродинамики.
- •Общий случай границы раздела сред.
- •Граница раздела диэлектриков.
- •Поле на поверхности идеального электрического проводника («электрическая стенка»).
- •Поле на поверхности идеального магнитного проводника («магнитная стенка»).
- •Поле на бесконечности («условие излучения»).
- •§1.3. Энергия электромагнитного поля. Теорема Умова-Пойнтинга.
- •§1.4. Излучение электромагнитных волн. Волновые уравнения. Электродинамические потенциалы и векторы Герца.
- •§1.5. Понятие о зонах излучения и диаграмме направленности источника электромагнитных волн
- •Понятие о диаграммах направленности
- •Поляризационные характеристики поля
- •§1.6. Элементарные излучатели Электрический вибратор
- •Магнитный вибратор
- •Элемент Гюйгенса
- •§1.7. Электромагнитные волны: плоские, сферические, цилиндрические – решения волнового уравнения
- •Плоские волны
- •Сферическая волна
- •Цилиндрическая волна
- •Особенности распространения волн в различных средах
- •§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение
- •Общие соотношения
- •Среды без потерь
- •Проводник с конечной проводимостью.
- •Идеальный проводник.
- •Понятие о поверхностном сопротивлении. Скин-эффект.
- •§1.9. Отражение плоской волны от границы раздела диэлектриков при произвольном угле падения
- •Параллельная поляризация
- •Перпендикулярная поляризация
- •Полное отражение и поверхностные волны.
- •§ 1.10. Важные теоремы
- •Принцип взаимности
- •Метод зеркальных отображений
- •Часть II. Теория линий передачи
- •§ 2.1. Применение теории цепей для анализа линий передачи
- •Волны напряжений и токов в линии передач
- •Линия передачи без потерь
- •§2.2. Применение теории электромагнитного поля для анализа линий передачи
- •Параметры линии передачи
- •Вывод телеграфных уравнений из уравнений Максвелла для коаксиальной линии
- •§2.3. Обобщенная линия передачи без потерь. Трансформация полного сопротивления и коэффициента отражения вдоль линии передачи
- •Короткое замыкание на конце линии
- •Холостой ход на конце линии
- •Полуволновый повторитель и четвертьволновый трансформатор
- •Соединение линий передачи с различными характеристическими сопротивлениями
- •§ 2.4. Диаграмма Смита
- •Диаграмма полных проводимостей.
- •Методика измерения полного сопротивления
- •§2.5 Понятие о согласовании сопротивлений
- •§2.6. Согласование посредством сосредоточенных параметров
- •Согласующие цепи на реактивных элементах
- •§2.7. Четвертьволновый трансформатор сопротивлений
- •§2.7. Многосекционные трансформаторы
- •Биномиальный многосекционный трансформатор
- •Многосекционный трансформатор Чебышева
- •§2.8. Шлейфные трансформаторы сопротивлений
- •Одношлейфовый трансформатор
- •Двухшлейфовый трансформатор
- •§2.9. Обобщенная линия передачи с потерями
- •Линия с низкими потерями
- •Линия передачи сигналов без искажений
- •Параметры нагруженной линии с потерями
- •Применение метода возмущений для определения постоянной затухания
- •Часть III. Электромагнитные волны в направляющих системах
- •§3.1. Классификация линий передачи и их основные характеристики
- •§3.2. Общая теория регулярных линий передачи произвольного поперечного сечения. Поперечные и волноводные волны.
- •Поперечные (tem) электромагнитные волны
- •Волноводные волны h- и e-типов
- •Влияние затухания в диэлектрике
- •§3.3. Двухпластинчатый волновод
- •Поперечные tem-волны
- •§3.3. Прямоугольный волновод
- •§3.4. Круглый волновод
- •§3.5. Двухпроводная линия передачи
- •§3.6. Коаксиальная линия передачи
- •Поперечные tem-волны
- •Высшие типы колебаний
- •§3.7. Поверхностные волны в металлизированной с одной стороны диэлектрической подложке
- •§3.8. Полосковые и микрополосковые линии передачи
Диаграмма полных проводимостей.
При анализе сложных цепей может возникнуть необходимость использовать не только полные сопротивления, но и полные проводимости. Покажем, что круговая диаграмма полных сопротивлений может быть трансформирована в диаграмму полных проводимостей.
Коэффициент отражения можно выразить через полную проводимость
![]() , (2.53)
, (2.53)
где
![]() - полная нормированная проводимость,
- полная нормированная проводимость,
![]() ,
,
![]() .
.
Рассмотрим
входное сопротивление линии, имеющей
длину
![]() (рис.2.12).
(рис.2.12).
![]() , (2.54)
, (2.54)
или ![]() .
.
Ф ормула
(2.54) является уравнением четвертьволнового
трансформатора, используемого для
узкополосного согласования. Как видно
из (2.54), входное нормированное сопротивление
линии передачи, длиной
ормула
(2.54) является уравнением четвертьволнового
трансформатора, используемого для
узкополосного согласования. Как видно
из (2.54), входное нормированное сопротивление
линии передачи, длиной
![]() ,
равно нормированной проводимости
нагрузки. Это означает, что поворачивая
каждую точку круговой диаграммы полных
сопротивлений на 180
(что соответствует перемещению вдоль
линии передачи на
,
равно нормированной проводимости
нагрузки. Это означает, что поворачивая
каждую точку круговой диаграммы полных
сопротивлений на 180
(что соответствует перемещению вдоль
линии передачи на
![]() ),
можно получить круговую диаграмму
полных проводимостей.
),
можно получить круговую диаграмму
полных проводимостей.
Методика измерения полного сопротивления
Пусть в линии передачи без потерь существует стоячая волна, как показано на рис. 2.13, а. Для определения сопротивления нагрузки необходимо знать волновое сопротивление линии, длину волны в линии, а также модуль и фазу коэффициента отражения.
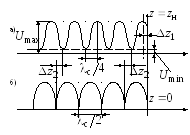
Рис.2.13. Методика измерения сопротивления нагрузки: а) стоячая волна при присоединенной измеряемой нагрузке, б) опыт короткого замыкания.
Перепишем выражения для сопротивления нагрузки и коэффициента отражения в следующем виде
![]() ;
;
![]() ;
;
![]() .
.
Длина
волны в линии
![]() и
и
![]() легко определяются из эксперимента.
Для фазовых соотношений на рис.2.13 можно
получить
легко определяются из эксперимента.
Для фазовых соотношений на рис.2.13 можно
получить
![]() ,
где
,
где
![]() - расстояние от плоскости подключения
нагрузки до пучности напряжения в линии.
Однако на практике это расстояние не
всегда удается измерить, поэтому
используется опыт короткого замыкания.
Для этого сначала подключают нагрузку
и фиксируют положение любого минимума
напряжения в линии
(рис. 2.13, а). Затем
нагрузку закорачивают и определяют
положение минимума напряжения, ближайшего
к ранее найденному со стороны генератора
(рис. 2.13, б). Расстояние между двумя
минимумами
- расстояние от плоскости подключения
нагрузки до пучности напряжения в линии.
Однако на практике это расстояние не
всегда удается измерить, поэтому
используется опыт короткого замыкания.
Для этого сначала подключают нагрузку
и фиксируют положение любого минимума
напряжения в линии
(рис. 2.13, а). Затем
нагрузку закорачивают и определяют
положение минимума напряжения, ближайшего
к ранее найденному со стороны генератора
(рис. 2.13, б). Расстояние между двумя
минимумами
![]() .
.
§2.5 Понятие о согласовании сопротивлений
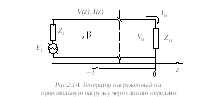


Р азличают
два вида согласования полных сопротивлений:
обычное и так называемое сопряженное.
Под обычным согласованием понимают
такое преобразование сопротивления
нагрузки, при котором в линии передачи
устанавливается режим чисто бегущей
волны. При сопряженном согласовании
под согласованной нагрузкой понимают
такую нагрузку для генератора, в которую
от генератора поступает максимальная
мощность.
азличают
два вида согласования полных сопротивлений:
обычное и так называемое сопряженное.
Под обычным согласованием понимают
такое преобразование сопротивления
нагрузки, при котором в линии передачи
устанавливается режим чисто бегущей
волны. При сопряженном согласовании
под согласованной нагрузкой понимают
такую нагрузку для генератора, в которую
от генератора поступает максимальная
мощность.
Рассмотрим СВЧ-цепь, представленную на рис.2.14, и ее эквивалентную схему в сечении А-А (рис.2.15)
Выразим величины элементов схем на рис.2.14 и рис.2.15
![]() ;
;
![]()
![]() ;
;
![]() .
.
В
эквивалентной схеме рисунка 2.15
![]() представляет собой полное сопротивление
в сечении А-А, измеренное в сторону
генератора, а
представляет собой полное сопротивление
в сечении А-А, измеренное в сторону
генератора, а
![]() - полное сопротивление, измеренное в
сторону нагрузки. Условие обычного
согласования (режим бегущей волны)
принимает вид:
- полное сопротивление, измеренное в
сторону нагрузки. Условие обычного
согласования (режим бегущей волны)
принимает вид:
![]() (2.55)
(2.55)
Для отыскания условия сопряженного согласования на основании эквивалентной схемы определим активную мощность, которая выделяется в сопротивлении нагрузки. Полный ток в эквивалентной схеме равен
![]() ,
,
а активная
составляющая мощности, выделяемая в
сопротивлении
![]() ,
имеет вид:
,
имеет вид:
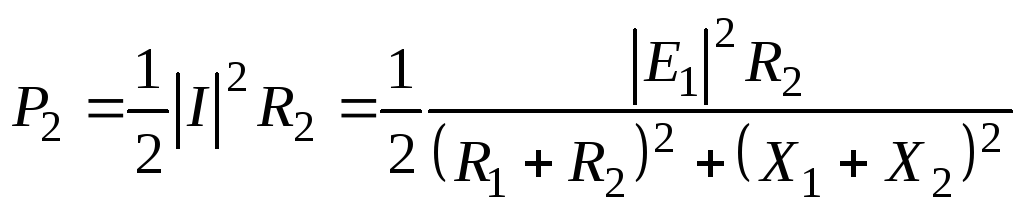 .
.
Будем
считать, что параметры генератора
фиксированы, так как они определяются
внутренним сопротивлением генератора
(![]() ).
).
В нагрузку будет поступать максимальная мощность при условии:
![]() .
.
Таким образом, условие сопряженного согласования можно записать в виде
![]() (2.56)
(2.56)
Одновременно равенства (2.55) и (2.56) могут быть выполнены лишь при условии:
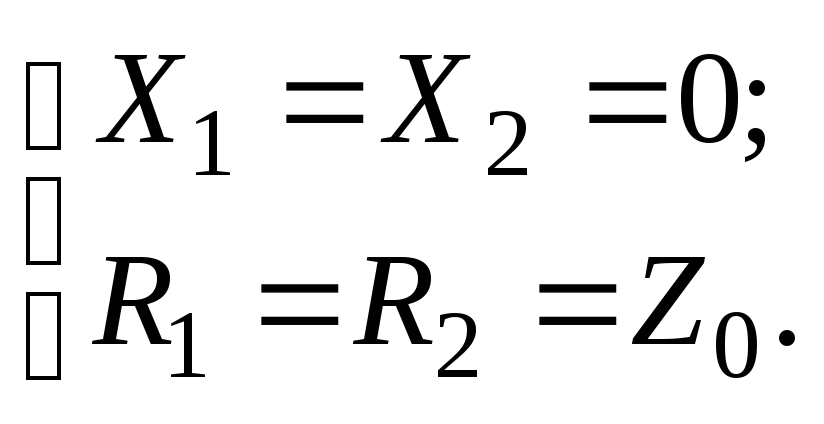 (2.57)
(2.57)
Соотношения (2.57), являющиеся условием оптимального согласования, на практике трудно реализовать. Поэтому предпочтение отдается режиму обычного согласования (2.55), т.к. рассогласование линий передачи, возникающее при условии максимальной отдачи мощности в нагрузку (2.56), возбуждает большую отраженную волну, которая может существенно изменить характеристики СВЧ-тракта.
Необходимость согласования линий передачи возникает в следующих случаях:
- к линии передачи присоединена заведомо рассогласованная нагрузка;
- при сопряжении линий передачи с разными волновыми сопротивлениями;
- в линию включаются какие-либо неоднородности.
Для получения согласования в разрыв линии должен быть включен согласующий четырехполюсник, как показано на рис.2.16.

Рис.2.16. Согласующий четырехполюсник
Согласующий четырехполюсник предназначается для устранения отраженной волны, т.е. преобразования в общем случае комплексного сопротивления нагрузки (в сечении 2 - 2) в сопротивление нагрузки в (сечении 1 - 1):
![]() ,
,
![]() .
.
На практике используют следующие типы согласующих четырехполюсников:
- поглощающие (диссипативные), или поглощающие ослабители (аттенюаторы);
- чисто реактивные, недиссипативные.
Поглощающие согласователи обеспечивают уменьшение отражения за счет рассеивания проходящей через них мощности, при этом существуют как взаимные (ослабление одинаково во обоих направлениях распространения), так и не взаимные (вентильные) аттенюаторы. Однако сам принцип действия таких схем является их главным недостатком – при прохождении через аттенюатор возникают потери мощности сигнала.
Поэтому с энергетической точки зрения более выгодно использовать реактивные четырехполюсники.
Рассмотрим теперь некоторые виды согласования, наиболее широко применяемые на практике.
