§ 2.4. Диаграмма Смита

Диаграмма Смита или круговая диаграмма полных сопротивлений, показанная на рис.2.10, является графическим приспособлением и широко применяется при расчете линий передачи. Данная диаграмма была впервые предложена сотрудником компании Белл П. Смитом в 1939г [9]. Современному читателю, однако, может показаться, что в наше время мощных компьютеров актуальность графического способа решения задач инженерных расчетов крайне мала. В ответ на это возражение стоит отметить, что изучение диаграммы Смита позволяет значительно проще и образней объяснить ряд явлений в линиях передачи, а также развить инженерную интуицию при решении задач согласования устройств СВЧ. Кроме того, диаграмма Смита является стандартным средством отображения параметров устройств в программах компьютерного проектирования и в измерительных приборах.

Рис.2.10. Диаграмма Смита

Круговая диаграмма устанавливает связь между коэффициентом отражения и полным сопротивлением в любой точке линии передачи. Они предназначены для расчетов однородных линий передач без потерь. Диаграммы строятся в комплексной плоскости коэффициента отражения.

Из формулы (2.39), учитывая (2.38), можно получить

, (2.48)

здесь - нормированное сопротивление нагрузки. Поскольку в общем случае - комплексная величина, то можно записать

,

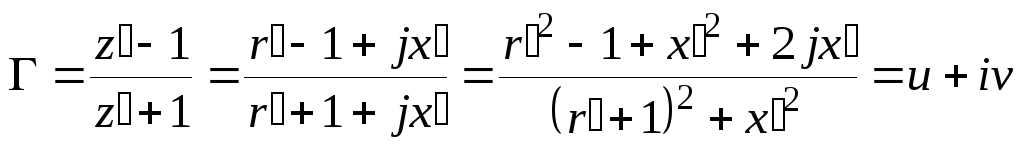где 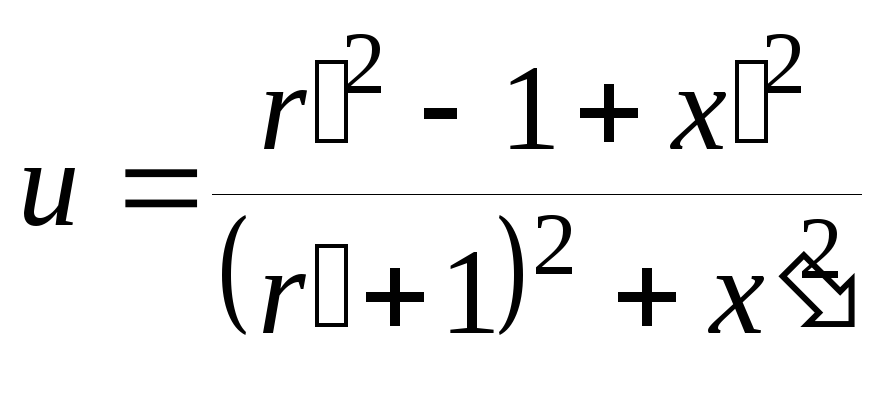, (2.49)

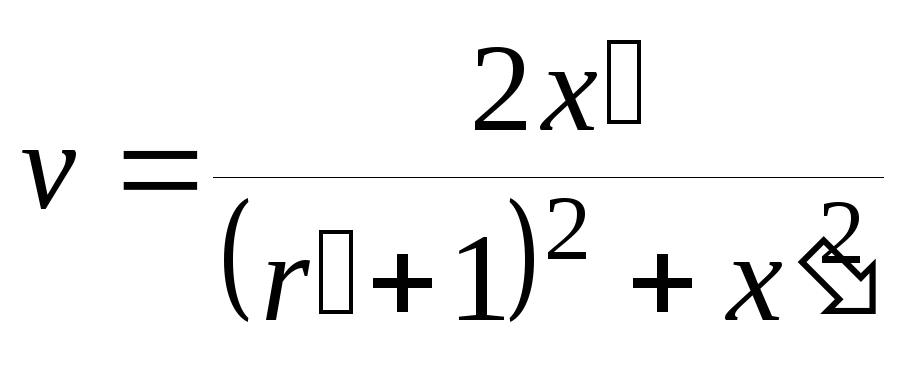. (2.50)

Поочередно исключая и из формул (2.49) и (2.50), можно получить уравнения окружностей:

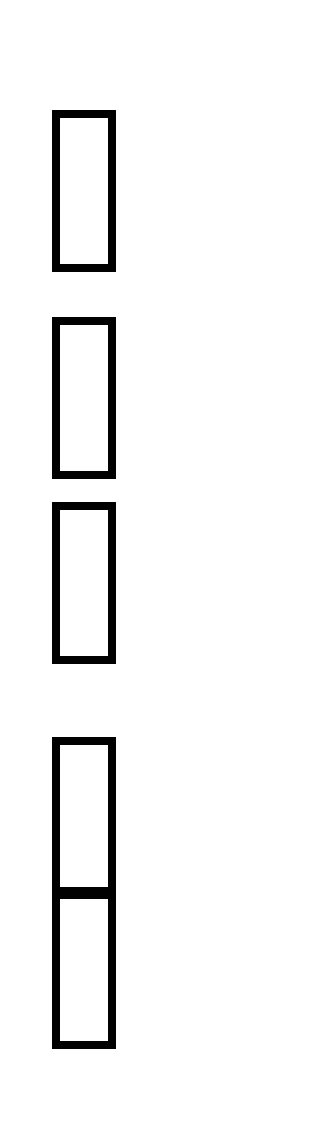
, (2.51)

(2.52)

Уравнение (2.51) дает семейство окружностей постоянных активных сопротивлений, построенное на рис.2.11,а, а уравнение (2.52) – семейство окружностей постоянных реактивных сопротивлений, показанное на рис.2.11,б.

Рис.2.11. Семейство окружностей постоянных активных (а) и реактивных (б) сопротивлений

Модуль и фаза коэффициента отражения образуют на круговой диаграмме полярную систему координат, относительно которой построены линии постоянных и . Используемой областью является область, ограниченная кругом единичного радиуса. Поскольку модуль коэффициента отражения вдоль линии передачи остается постоянным, то полное сопротивление при движении вдоль линии передачи преобразуется вдоль окружности с центром в начале координат. Семейство таких окружностей представляет собой линии постоянных .

Диаграмма Смита получается наложением диаграмм на рис.2.11, а и б. На периферии круга наносят шкалу углов. За начало отсчета углов принимают точку и . Углы выражают в виде отношения длины линии l к длине волны в данной линии . Для удобства применяются две шкалы углов: “К генератору” и “К нагрузке”.

Вертикальная прямая на круговой диаграмме является линией чисто активных сопротивлений. Учитывая, что в каждой точке этой прямой , а , то легко показать, что КСВН равен при и равен при . Таким образом, линии постоянных значений КСВН совпадают с линиями постоянных значений и являются окружностями с центром в середине диаграммы. Графически КСВН определяется в точке пересечения указанных окружностей и прямой чисто активных сопротивлений.