Особенности распространения волн в различных средах

Рассмотрим теперь особенности распространения волн в средах без потерь, в среде с потерями и в проводнике.

Указанные особенности определяются видом волнового числа и характеристическим сопротивлением сред.

Рассмотрим среду без потерь. В данной среде  и  являются чисто действительными величинами, следовательно, волновое число и характеристическое сопротивление , также чисто действительные величины.

В среде с потерями волновое число становиться комплексной величиной. Ограничимся рассмотрением сред с диэлектрическими потерями, поскольку в СВЧ технике разработчикам аппаратуры в подавляющем большинстве случаев приходится иметь дело именно с ними.

В этом случае ¹. Введем понятие комплексной постоянной распространения

(1.119)

Предположим для простоты, что плоская волна, имеющая только компоненту электрического поля вдоль оси х, распространяется вдоль оси z. В этом случае уравнение (1.61) представляется в виде

(1.120)

и имеет решение

. (1.121)

При этом первое слагаемое определяет волну, бегущую в положительном направлении оси z., и с учетом времени может быть представлено в виде

.

Таким образом, последнее выражение определяет волну бегущую в положительном направлении оси z, с фазовой скоростью , имеющую длину волны , и затухающую с вдоль направления распространения с постоянной затухания . Волна бегущая в противоположном направлении затухает вдоль координаты с – z. В случае, когда потерь нет , т.е. , .

Определим соответствующую компоненту вектора H, применяя второе уравнение Максвелла или формулу (1.109), с учетом наличия двух волн, бегущих в противоположных направлениях

. (1.121)

При этом характеристическое сопротивление среды определяется как

, (1.122)

а выражение (1.121) можно переписать в виде

. (1.123)

Во многих практически важных задачах требуется оценивать потери в металлических проводниках, имеющих очень большую, но все же конечную проводимость. В металле токи проводимости существенно превосходят токи смещения и поляризации, т.е. . Тогда

. (1.124)

Определим глубину проникновения поля внутрь металла как, расстояние вдоль, которого напряженность поля уменьшается в . Поскольку множитель затухания , имеем

(1.125)

Величина называется толщиной скин-слоя¹, а эффект концентрации поля в скин-слое – скин-эффектом, имеющим большое практическое значение поскольку позволяет изготавливать очень тонкие проводники для миниатюрных устройств СВЧ.

Характеристическое сопротивление в металле

. (1.126)

Стоит заметить, что фаза характеристического сопротивления металлов равна 45, фаза материала без потерь 0. Следовательно, фаза характеристического сопротивления произвольного материала с диэлектрическими потерями лежит между 0 и 45.

§1.8. Отражение плоской волны от границы раздела сред. Нормальное падение

Расчет многих устройств СВЧ, а также радиотрасс, требует рассмотрения поведения волн на границе раздела сред с различными параметрами, при этом описание строится с применением понятий комплексных коэффициентов отражения и прохождения. Исследование указанных понятий начнем с рассмотрения вопроса нормального падения плоской волны на границу раздела свободного пространства и среды с потерями, занимающей полупространство z > 0 и описывающейся параметрами ,  и  (рис.1.18).

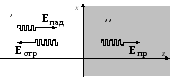
Рис. 1.18. Отражение плоской волны от среды с потерями при нормальном падении на границу раздела