1.3. Частные случаи движения точки

1. Равнопеременное движение.

Если т.е. ускорение не меняется как по величине, так и по направлению, то движение называют равнопеременным. В этом случае

(вывод)

(3.1)

где - начальная скорость, а - начальное перемещение. В этом случае

_ср.

Отметим, что при решении задач начальное перемещение всегда можно сделать равным нулю, поместив начало отсчета в начало движения.

2. Прямолинейное равномерное движение.

Если = const, то движение называют равномерным.

В случае прямолинейного равномерного движения не меняется и направление скорости, т.е. ==_ср (). Тогда уравнения (3.1) упрощаются и принимают вид

(3.2)

После проектирования на ось ОХ сонаправленную с перемещением получим

v_x=v_ox,

. (3.3)

3. Прямолинейное равнопеременное движение.

a_x=const.

В этом случае справедливы общие уравнения равнопеременного движения (3.1). После проектирования на ось ОХ сонаправленную с перемещением и начальной скоростью они принимают вид

На рис.4.2 изображены графики зависимостей а_х(t), v_х(t), х(t) при равноускоренном (а_х>0, случай а), равномерном (а_х=0, случай б) и равнозамедленном (а_х<0, случай в) движении при х₀=0, v₀=0.

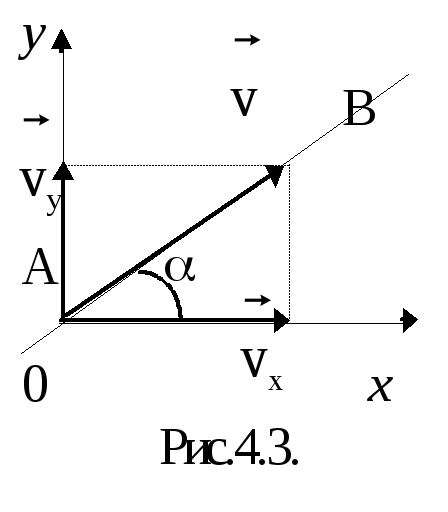
Любое равномерное движение, происходящее с постоянной скоростью вдоль произвольной прямой АВ (рис.4.3), можно разложить на два независимых равномерных и прямолинейных движения вдоль осей ОХ и ОY со скоростями v_x и v_y: х= х_оv_xt, y= y_ov_yt, где v_x=v cos , v_y=v sin .

Скорость тела в любой точке траектории и направлена вдоль траектории движения. И наоборот, если движение состоит из нескольких движений со скоростями

Последнее выражение называют правилом сложения скоростей.

1.4. Криволинейное движение точки

Криволинейное движение – движение, при котором траектория – кривая линия. Если материальная точка движется по произвольной кривой, то эту кривую можно разбить на малые дуги и каждую из них совместить с дугой некоторой окружности. Каждая такая окружность называется окружностью кривизны, а радиус называется радиусом кривизны траектории в данной точке.

Поэтому достаточно рассмотреть движение материальной точки по окружности.

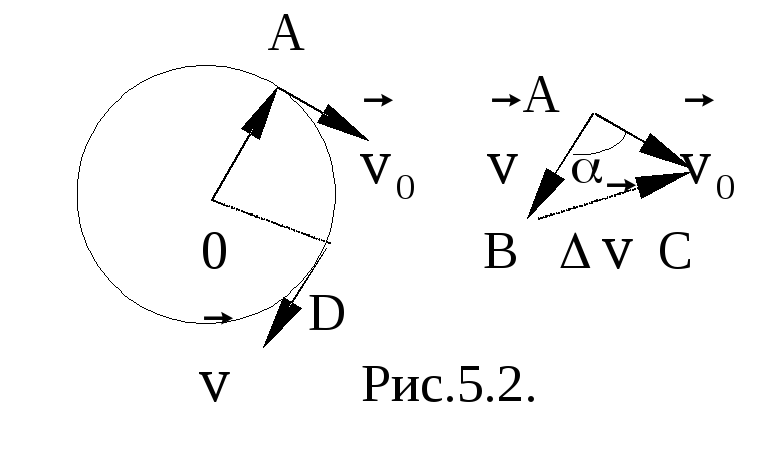
1 случай: равномерное движение по окружности, когда скорость по величине является постоянной ||=const, но изменяется по направлению (см. рис.5.2). В этом случае 0, поэтому материальная точка движется с ускорением (т.к. ). Рассмотрим треугольник АВС. Он равнобедренный со стороной ||=v и основанием v, причем . Если точка D стремится к точке А, то угол в вершине АВС 0. Но углы при основании АВС равны (равнобедренный). Так как сумма всех углов АВС равна 180⁰, то углы при основании будут стремиться к 90⁰ каждый, то есть в пределе , тогда и ускорение будет перпендикулярно вектору скорости () и направлено к центру окружности. Длина вектора ||=. Длина дуги DA=, а время, за которое точка пройдет этот путь . Тогда модуль среднего ускорения . Используя первый замечательный предел , определим мгновенное ускорение: , то есть .

Нормальное (центростремительное) ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения направлен по радиусу к центру окружности.

2 случай. Скорость движущейся по окружности материальной точки изменяется по величине и направлению: .

–полное изменение скорости; – изменение скорости по направлению, – изменение скорости по величине. Из CED  . Поделим обе части этого равенства на перейдем к пределу: .

 .

Первое слагаемое является нормальным ускорением, второе – тангенциальное ускорение, направленное по касательной к траектории. Его величина

.

– если движение ускоренное; – если движение замедленное (рис.5.4).

Итак, при любом криволинейном движении полное ускорение можно представить в виде двух составляющих:

1. нормальное ускорение – характеризуется изменением скорости по направлению;

2. тангенциальное ускорение характеризуется изменением скорости по величине. Так как компоненты и взаимно перпендикулярны, то

ρ – кривизна траектории в данной точке.

Найти полное ускорение – это значит найти не только его величину, но и его направление в пространстве: , или .