Теорема 13 (Лагранжа).

Пусть функция непрерывна на отрезке и имеет производную на интервале . Тогда существует на интервале точка , для которой выполняется равенство

Доказательство. Теорема Лагранжа имеет простой геометрический смысл, если ее записать в виде

То есть теорема Лагранжа утверждает, что на графике всегда найдется точка , что касательная к ней параллельна хорде, стягивающей концы кривой .

Правило Лопиталя.

Пусть и определены и дифференцируемы в окрестности точки , за исключением, быть может, самой точки , , и в этой окрестности. Тогда, если существует , то существует и имеет место равенство

Доказательство. Будем считать, что конечное число. Доопределим функции и в точке , полагая . Тогда эти функции непрерывны в точке . Рассмотрим отрезок , где , или . На функции и непрерывны, а на дифференцируемы, поэтому по теореме Коши существует точка такая, что

Когда , то и , поэтому, в силу условия теоремы имеем

при условии, что предел в правой части равенства существует.

Этим теорема доказана.

Если выражение снова представляет собой неопределенность , то можно

Это относится и к неопределенности типа .

14. Применение дифференциального исчисления к исследованию функций. Локальный экстремум функции

Необходимое и достаточное условие постоянства функции выражается равенством , т.е.

Е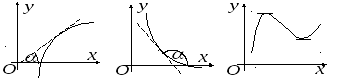 сли в данном промежутке производная функции положительна, то функция возрастает в этом промежутке; если производная отрицательна, то функция убывает в соответствующем промежутке.

Функция достигает в точке локального максимума (минимума), если можно указать такое , что ее приращение в точке удовлетворяет неравенству

(соответственно ).

По теореме Ферма, если функция достигает в точке локального экстремума и в этой точке производная существует, то она равна нулю

По определению такая точка называется стационарной. Это условие является необходимым для того, чтобы дифференцируемая функция имела локальный экстремум, но не достаточным.

Достаточные критерии локального экстремума.

Теорема. Пусть - стационарная точка функции (т.е. ) и имеет вторую непрерывную производную в окрестности . Тогда:

если , то есть точка локального максимума ;

если , то есть точка локального минимума .

Теорема. Пусть и и непрерывна в окрестности точки , тогда:

если - четное и , то имеет в локальный максимум;

если - четное и , то имеет в локальный минимум;

если - нечетное и , то заведомо не имеет в локального экстремума.

Кроме того. Если первая производная функции при переходе через точку меняет знак, то имеет в точке минимум, если знак меняется (при возрастании ) с «-» на «+», и максимум, если знак меняется с «+» на «-».

Вогнутость, выпуклость, точки перегиба.

К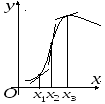ривая обращена в точке выпуклостью кверху (книзу), если существует окрестность такая, что для всех точек этой окрестности касательная к кривой в точке расположена выше (ниже) самой кривой (см. рис.).

Точка есть точка перегиба кривой , если при переходе через точка кривой переходит с одной стороны касательной на другую.

Теорема. Если функция имеет в точке вторую непрерывную производную и (), то кривая обращена в выпуклостью книзу (кверху).

Доказательство вытекает из понятия локального максимума, минимума.

Если функция такова, что производная непрерывна в , а и , то кривая имеет в точку перегиба.

Асимптоты графика функции.

Прямая называется вертикальной асимптотой , если (см. рис.).

Прямая называется наклонной асимптотой непрерывной функции , если .

Линия называется асимптотической кривой для , если .

Пример. Построить график функции . Составим таблицу

	возрастает асимптота		убывает	вертикальная асимптота	убывает		возрастает асимптота
	выпукла кверху		выпукла кверху		выпукла книзу		выпукла книзу

График имеет вид.

FVB