Обратная функция

Итак, каждому по определенному закону ставится в соответствие единственное значение . С другой стороны, каждому соответствует одно, или несколько значений .

В случае, когда каждому по некоторому закону соответствует только одно значение , получаем функцию

заданную на множестве со значениями во множестве . Эту функцию называют обратной функцией, по отношению к функции . Эти функции называются взаимно обратными. Для них выполняются тождества

Например. .

Некоторые свойства функций

1. Функция называется четной, если

.

2. Функция называется нечетной, если

.

3. Функция называется периодической если и (существует такое число "М" больше нуля, что для любого "х" принадлежащего множеству "А" выполняется равенство ).

4. Функция возрастает, если .

5. Функция неубывающая, если .

6. Функция убывает, если .

7. Функция невозрастающая, если .

8. Функция ограничена сверху на множестве , если .

9. Функция ограничена снизу на множестве , если .

Определение. Функция – ограничена, если она ограничена сверху и снизу.

Основные элементарные функции

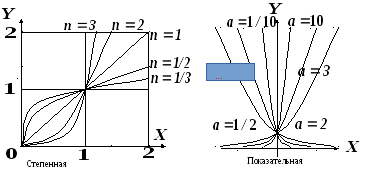
Элементарные функциями называют все функции, которые можно получить из основных элементарных с помощью алгебраических действий и образования сложных функций.

3. Предел числовой последовательности

Пусть каждому натуральному числу по некоторому закону поставлено в соответствие действительное или комплексное число . Тогда этим задана последовательность

Отдельные числа последовательности называются ее элементами.

Надо иметь ввиду, что и при считаются отличными как элементы последовательности, хотя не исключено, что как числа они равны между собой.

Определение. Число называется пределом последовательности , если для всякого найдется (зависящее от ) число такое, что выполняется неравенство

для всех (натуральных) .

В этом случае пишут

и говорят, что переменная или последовательность имеет предел, равный числу , или стремится к . Говорят также, что переменная или последовательность сходится к числу .

Геометрический смысл предела

О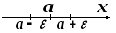пределение предела имеет следующий геометрический смысл: число является пределом последовательности , если в любой его - окрестности содержатся почти все члены , или вне этой окрестности находится лишь конечное число членов данной последовательности.

Пример 1. Дана последовательность . Предел этой последовательности , т.е. . Действительно, зададим произвольное число и решим неравенство

Этим для всякого найдено число такое, что неравенство выполняется для всех .

Пример 2. Дана последовательность . Предел этой последовательности , т.е. . В самом деле, составим неравенство . Оно, как мы видели, выполняется для любого , если .

Свойства пределов числовых последовательностей

1. Предел постоянной равен самой постоянной - .

2. Последовательность не может иметь двух различных пределов, если предел существует, то он единственный.

Доказательство от противного. Допустим, что имеет два различных предела и . Покроем точки и соответственно интервалами и настолько малой длины, чтобы эти интервалы не пересекались.

Т ак как , то в интервале находятся все элементы , за исключением конечного их числа. Но тогда интервал не может содержать в себе бесконечное число элементов и не может стремиться к . Мы пришли к противоречию, теорема доказана.

3. Если последовательность сходится (имеет предел), то она ограничена.

Доказательство. Пусть . Зададим и подберем натуральное число так, чтобы

Но тогда и выполняется неравенство

для всех . Пусть наибольшее из чисел

Тогда, очевидно,

Теорема доказана.