Односторонние пределы

По определению число называется пределом функции в точке справа (слева), если она определена на некотором полуинтервале () и для нее существует

для любой указанной последовательности .

Предел справа (слева) функции в точке принято обозначать так:

Если определена на интервале , то в точке может иметь смысл только число , а в точке - только число .

Равенства эквивалентны существованию предела .

6. Бесконечно большие и бесконечно малые функции

Функцию, для которой называется бесконечно большой при .

Функцию, для которой называется бесконечно малой при .

Свойства бесконечно малых величин.

1. Сумма бесконечно малых величин есть бесконечно малая величина.

2. Произведение двух бесконечно малых величин есть бесконечно малая величина.

3. Произведение бесконечно малой величины на константу есть бесконечно малая величина.

Будем рассматривать две функции и , заданные в некоторой окрестности точки , за исключением, быть может, самой точки . Будем считать, что на . Если то этот факт записывают так: , и говорят, есть от при .

Например

Выражение , обозначает бесконечно малую при .

Свойство отражает тот факт, что функцию можно записать в виде , где при .

Если функции и сами бесконечно малые, то символ (по старинной терминологии) означает бесконечно малую, более высокого порядка .

Если функции и суть бесконечно большие, то символ (по старинной терминологии), означает бесконечно большую более высокого порядка .

Кроме того, пишут

и называют функции и эквивалентными (асимптотически равными) при , если выполняется свойство:

Например.

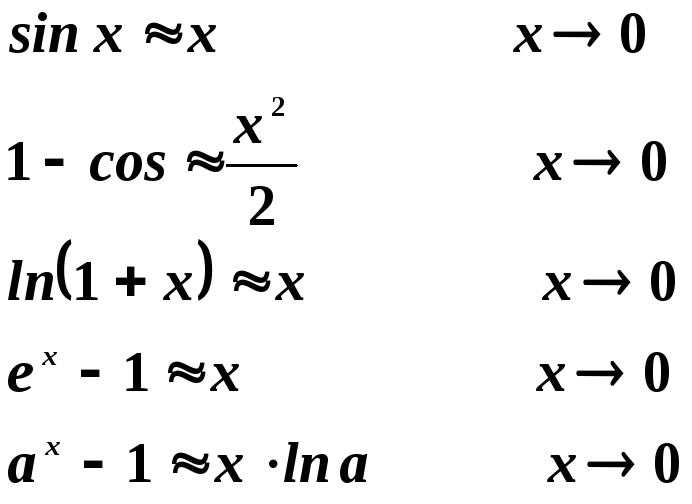
Теорема. Если

то

Доказательство. Если на и выполняется условие теоремы, то, очевидно, и . Но тогда

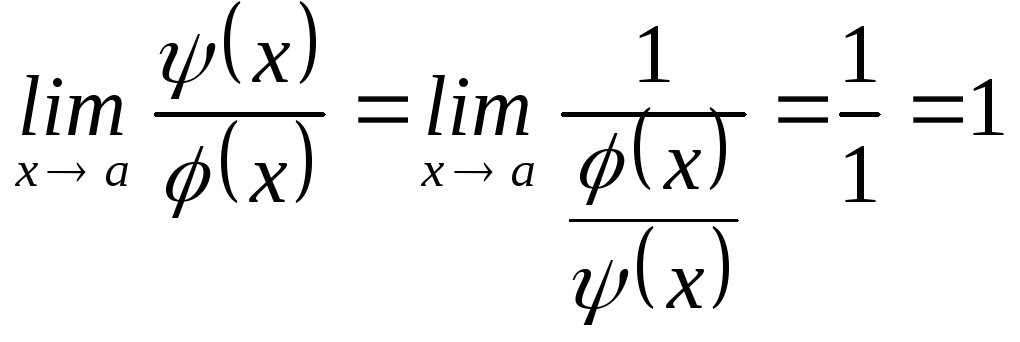
Теорема. Если

то

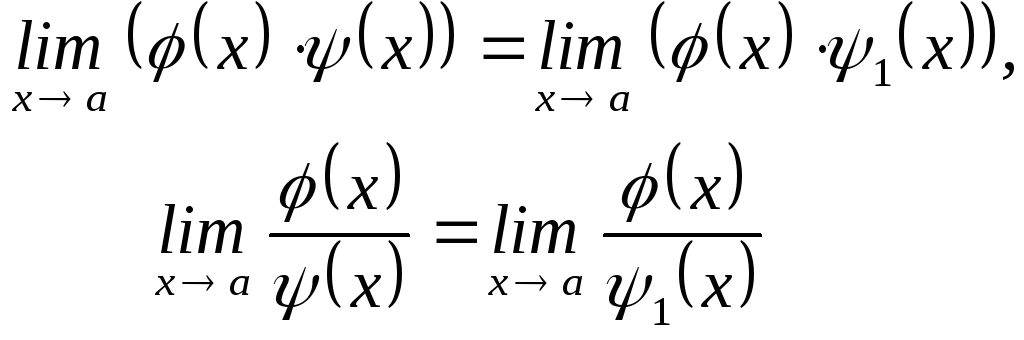
Эти равенства надо понимать в том смысле, что если существует в них предел справа, то существует предел и слева, и они равны, и обратно.

Отсюда следует, что если какой-либо из этих пределов не существует, то не существует и второй.

Пример. , потому, что

Пример.

7. Замечательные пределы

1.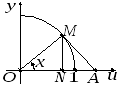

Доказательство. Так как функция является непрерывной, то при . Поэтому выражение представляет собой неопределенность типа . Раскроем эту неопределенность. Согласно рисунку можно записать

при

так как из рисунка вытекает , , , . Отсюда, разделив на , получим

или

Функция непрерывная, поэтому

И, следовательно, .

2.

Рассмотрим вначале вспомогательную последовательность

Эта последовательность возрастающая, и ограничена сверху. Действительно, на основании формулы бинома Ньютона имеем:

Отсюда

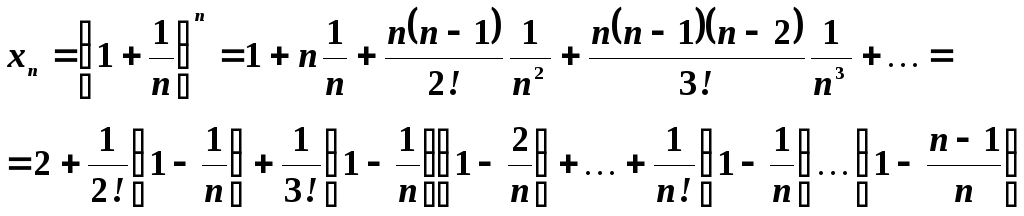
Из данного равенства видно, что последовательность . Докажем, что последовательность ограничена сверху. Из предыдущего следует, что

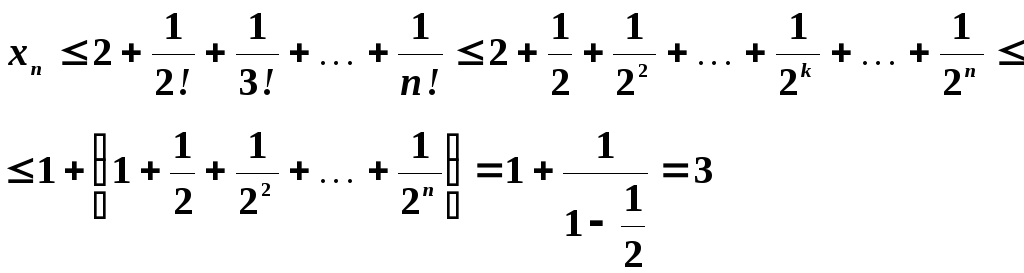
Так как в скобках стоит геометрическая прогрессия с показателем , а сумма геометрической прогрессии равна .

Покажем теперь, что последовательность возрастающая. Можно записать

Сравнивая и , видим, что , так как каждое слагаемое в больше слагаемого в и, кроме того, в имеется на одно положительное слагаемое больше.

Следовательно, последовательность сходится. Обозначим предел этой последовательности буквой , как это впервые предложил Л.Эйлер

Доказательство. Мы должны показать, что

Это равенство справедливо, если - натуральное число. Пусть теперь - произвольное число, стремящееся к бесконечности. Пусть - целая часть числа . Тогда . В этом случае

При , , следовательно, первый и последний член цепочки неравенств стремятся к . Поэтому

Так как при этом , то мы доказали исходное при .

Если теперь , то введем новую переменную и

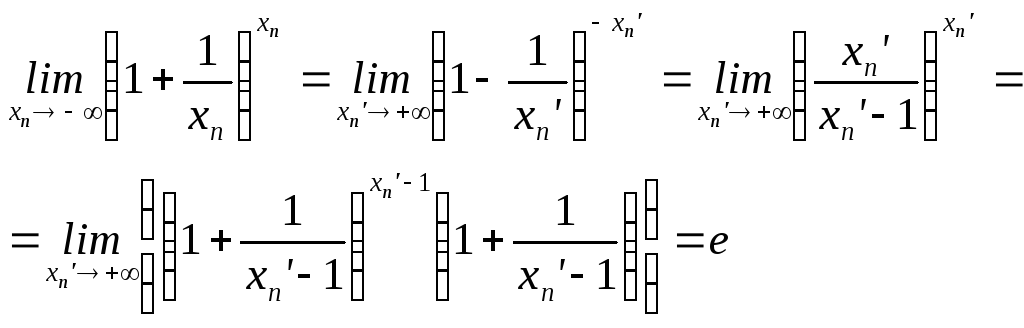
Тем самым теорема доказана.

Пример. . Получается из второго замечательного предела заменой .

Пример.

Если , то и

Пример. , .

Доказательство.

Пример. , .

Доказательство. Положим . Тогда