5.3. Квадратурная формула Ньютона – Котеса
Простой (но в то же
время универсальный) прием построения
квадратурных формул состоит в том, что
подынтегральная функция
аппроксимируется на отрезке
интерполяционным многочленом, например
многочленом Лагранжа
,
т.е. получается приближенное равенство:
,
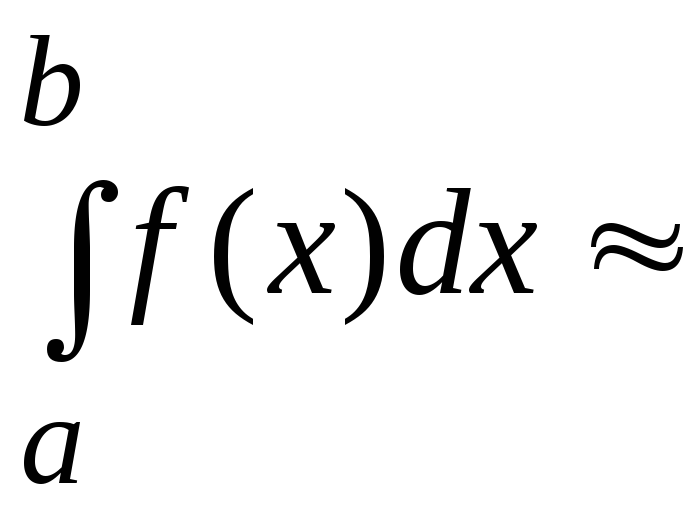
(5.5)
что позволяет свести
вычисление интеграла от сложной функции
к интегрированию многочлена. Подставляя
вместо
его представление, получаем:
=
.
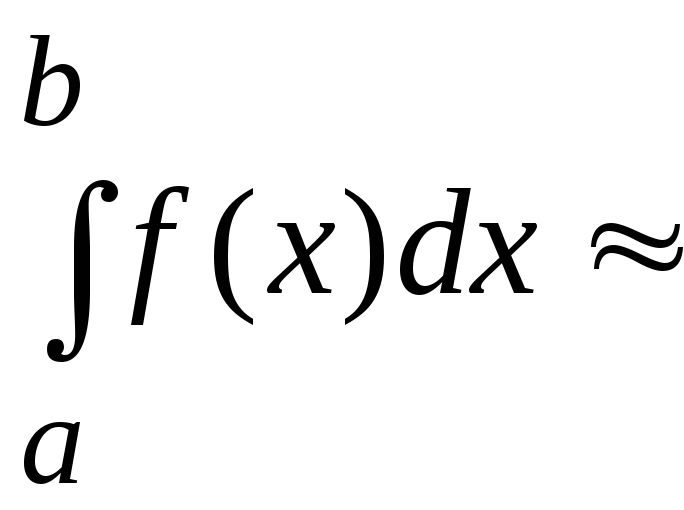
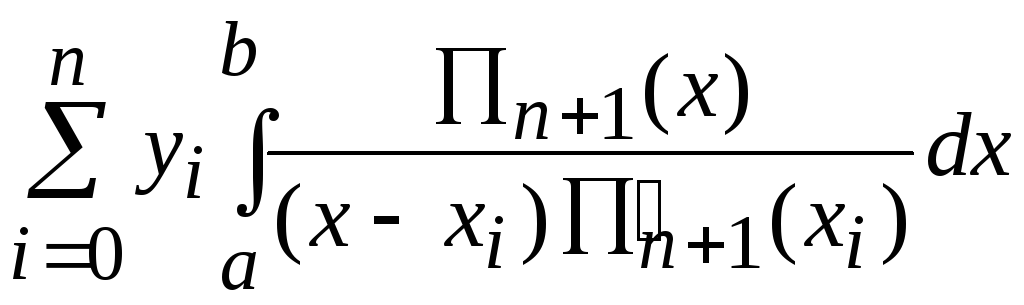(5.6)
Замечания к (5.6):
а) коэффициенты
не зависят от
(составлены с учетом узлов интерполирования
);
б) если
– полином степени n,
то (5.6) точная, т.к.
.
Коэффициенты
можно преобразовать к более удобному
для практического применения форме.
Для этого воспользуемся соотношением
.
(5.7)
В результате применения (5.7) получим следующие выражения:
,
dx
= hdq
=
.
При
имеем q
= 0, а при
будем иметь
.
Затем, если введем
обозначения
(назывемыми коэффициентами
Котеса) как:
,
i
= 0, 1, …, n,
(5.8)
окончательно получаем:
=
,
(5.9)
которые не зависят
от функции
,
а только от числа n
точек разбиения.
На основе (5.9) получаем квадратурную формулу Ньютона – Котеса:
,
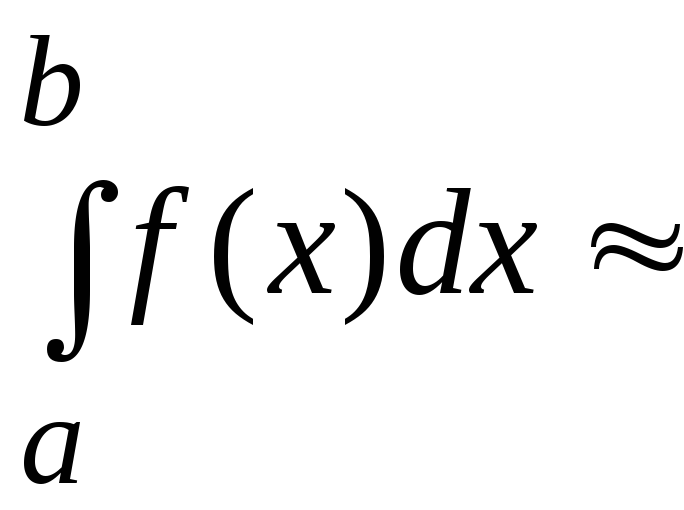
(5.10)
дающих на одном участке интегрирования различные представления для различного числа n отрезков разбиения.
5.4. Метод трапеций.
При n = 1 из формулы (5.8) получаем (i = 0, 1):
=
=
,
=
.
Тогда по формуле
(5.10) на отрезке [
:
]
получаем интеграл:
= (
–
)
=
(
+
).
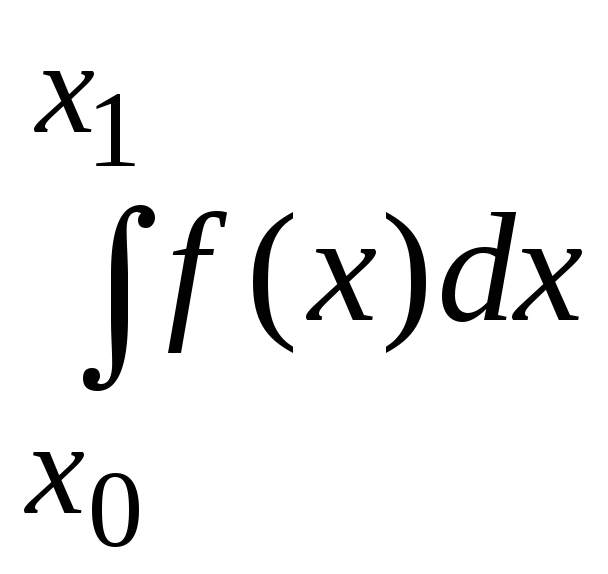(5.11)
Геометрическая интерпретация (5.11) дана на рис. 5.2.
Если последовательно
соединять точки
отрезками прямых, то график функции
представится в виде ломаной, и площадь
фигуры, ограниченной этой ломаной, осью
абсцисс и прямыми x
= a,
x
= b,
будет складываться из суммы площадей
элементарных прямолинейных трапеций
с основаниями
и боковыми сторонами
и
(i
= 1, 2, …, n)
(Рис. 6.2). С известным приближением можно
считать, что определенный интеграл
равен этой сумме, потому что при
неограниченном увеличении числа точек
деления и стремления к нулю всех элементов
верхняя граница фигуры (ломаная) переходит
в линию
.
(Получившуюся фигуру называют криволинейной
трапецией, и
площадь этой фигуры равен определенному
интегралу.) Так как площади прямолинейных
трапеций вычисляются как
,
то, складывая эти величины, получаем
формулу
трапеций для
численного интегрирования:
.
Рис. 5.2 Рис. 5.3
Важный частный
случай применения этой формулы –
численное интегрирование с постоянным
шагом
const
(i
= 1, 2, …, n):
.
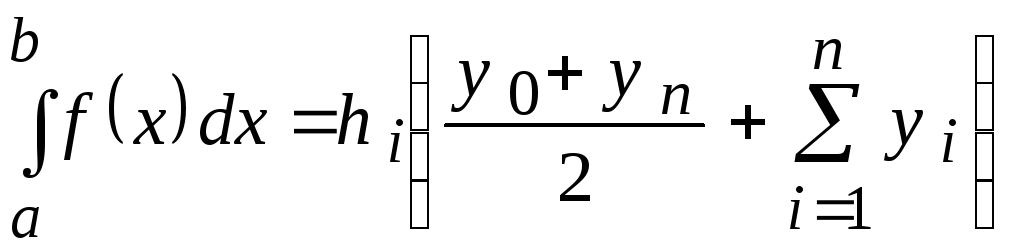Формула трапеций обладает преимуществом большой простоты и достаточно точна, если данные задачи приводятся с небольшим числом значащих цифр, но, как правило, точность метода трапеций ниже точности метода средних. Заметим также, что характер погрешностей формул прямоугольников и трапеций различен. Если учесть характер этих погрешностей, то можно получить уточненное значение интегралов.
Обозначим определенный
интеграл, вычисленный с применением
формулы прямоугольников через
,
а вычисленный по формуле трапеций –
через
.
Тогда уточненная формула будет следующая:
. (1)
Результат применения этой формулы обычно имеет высокую точность (если сравнить результат вычисления определенного интеграла для берущейся подынтегральной функции с результатом вычисления определенного интеграла от этой же функции с использования формулы (1), часто с точностью до погрешностей округления результаты совпадают).