10. Числовые характеристики случайного вектора
1.Как определяются начальные моменты случайного вектора?
2.Как определяются центральные моменты случайного вектора?
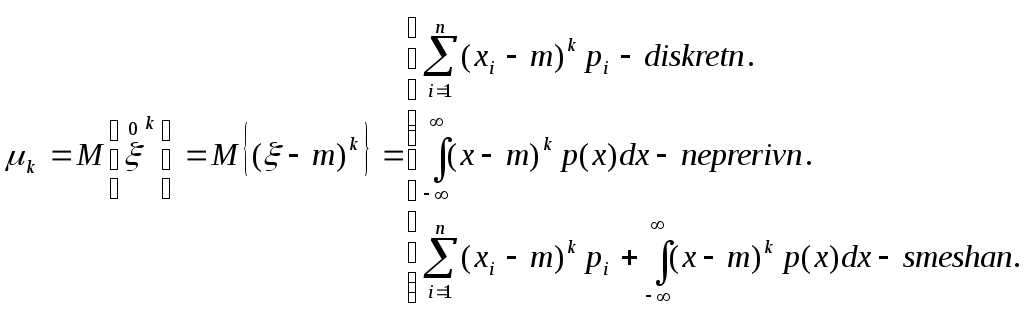
3.Дать определение корреляционного момента.
Корреляционный момент характеризует степень тесноты линейной зависимости величин X и Y и рассеивание их значений относительно точки (mX, mY).
4.Перечислить основные свойства корреляционного момента.
5.Записать формулу для вычисления корреляционного момента дискретных случайных величин.
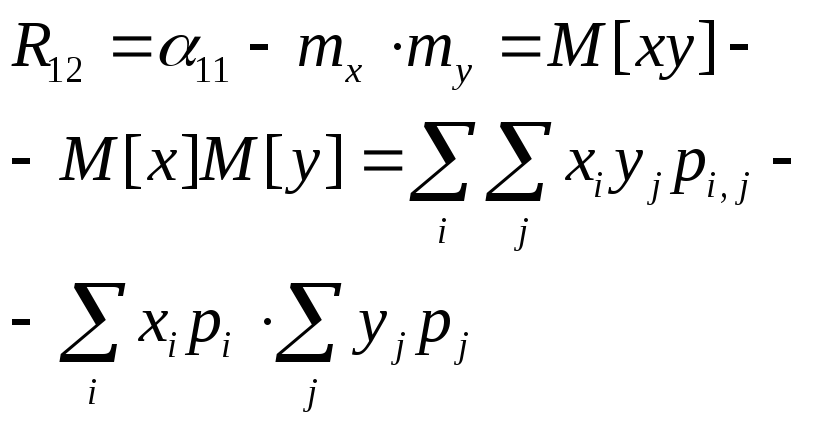
6.Записать формулу для вычисления корреляционного момента непрерывных случайных величин.
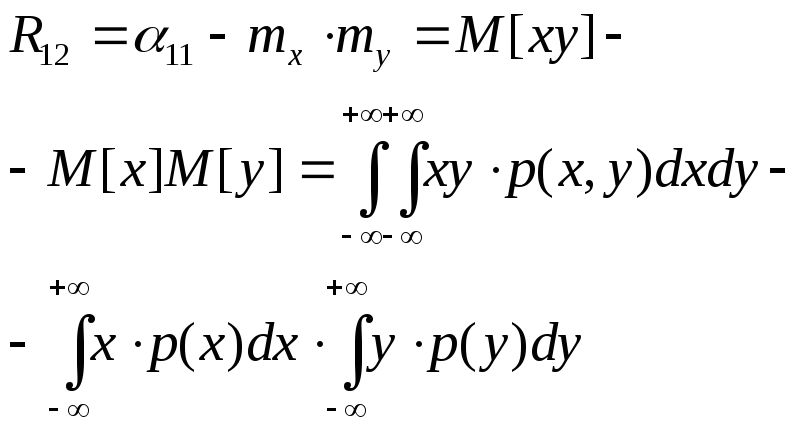
7.Чему равна дисперсия суммы двух случайных величин?
,
если величины независимые.
8.Чему равно математическое ожидание произведения двух случайных величина?
,
если величины независимые.
9.Как связаны понятия независимости и некоррелированности случайных величин? Обосновать ответ.
Если величины независимы – они некоррелированы, но обратное в общем случае неверно:
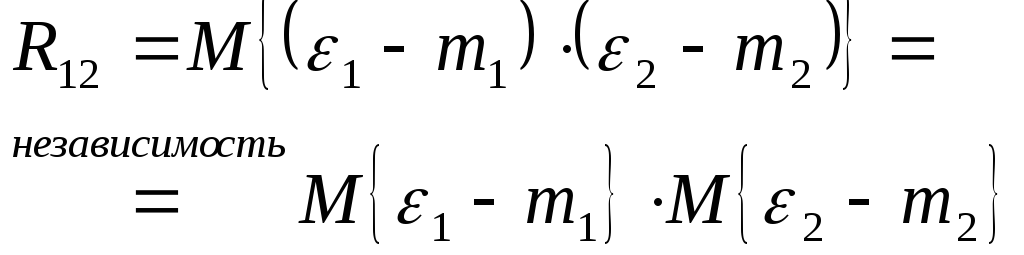
10.Дать определение коэффициента корреляции.
Коэффициент
корреляции
характеризует
степень линейной зависимости величин
и равен:
11.Перечислить основные свойства коэффициента корреляции.
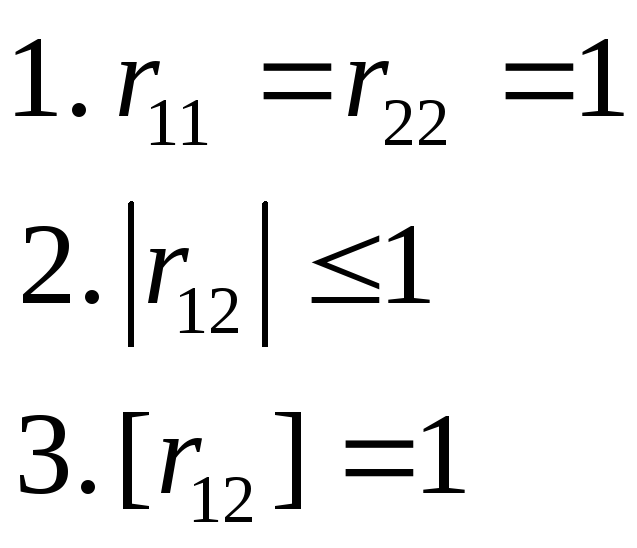
12.В каких границах могут находиться значения корреляционного момента и коэффициента корреляции?
13.Чему равен коэффициент корреляции двух случайных величин, связанных линейной зависимостью?
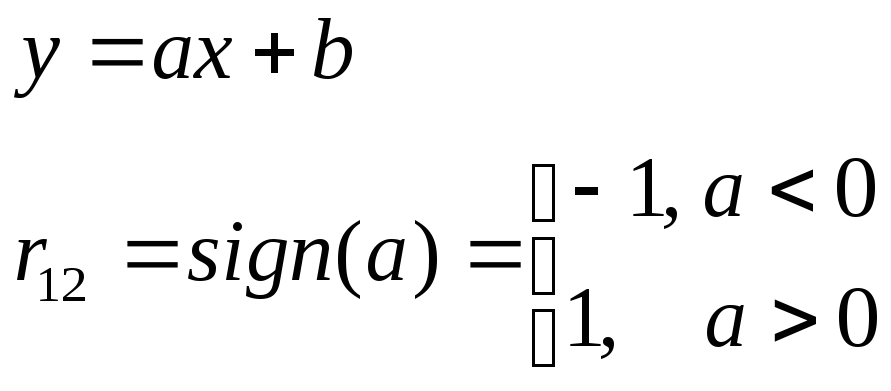
14.Каков смысл корреляционного момента и коэффициента корреляции?
Корреляционный
момент
характеризует
степень тесноты линейной зависимости
величин X
и
Y
и
рассеивание их значений относительно
точки (mX,
mY).
Коэффициент
корреляции
характеризует
степень линейной зависимости величин
15.Дать определение корреляционной матрицы. Какие у нее свойства?
Корреляционной матрицей называется матрица такого вида:
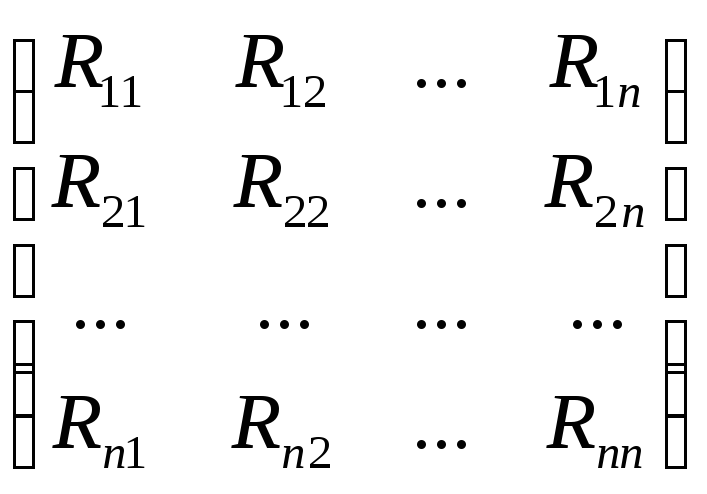
со следующими свойствами:
|
ξ |
1 |
2 |
… |
k |
… |
|
Р |
е- λ |
λ е- λ |
… |
(λk /k!)е- λ |
… |
16.Дать определение матрицы коэффициентов корреляции. Какие у нее свойства?
Матрицей коэфициентов корреляции называется матрица такого вида
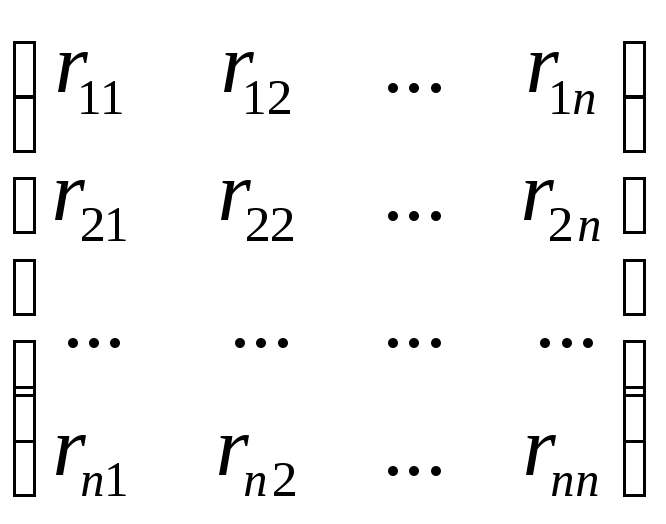
со следующими свойствами:
11. Основные распределения случайных величин
1. Вырожденное распределение и его характеристики.
Случайная величина ξ имеет вырожденное распределение с параметром а, и пишут ξ Ic если ξ принимает единственное значение а с вероятностью 1, то есть P(ξ = c) = 1.
1. Первая причина по которой исп. выр. величины: что в множество СВ. входят в качестве подмножеств обычные числа
2. Вырожденное распределение является моделью идеального измерительного прибора.
M{ ξ}=c D{ ξ}=0
2. Дать определение распределения Бернулли.
Случайная величина ξ имеет распределение Бернулли с параметром р, и пишут ξ Вр, если ξ принимает значения 1 и 0 с вероятностями р и 1 - р, соответственно. Случайная величина ξ с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха (0 успехов или 1 успех).Распредиление Бернулли является индикатором некоторого события.
3. Вычислить математическое ожидание и дисперсию случайной величины, имеющей распределение Бернулли.
M{
ξ}=0*q+1*p=p D{
ξ}=
-
=p-
=p(1-p)=pq
=M{
}=0*0*q+1*1*p=p
4. Дать определение биномиального распределения.
Говорят, что случайная величина ξ имеет биномиальное распределение с параметрами n и p, где 0 p , n и пишут ξ Вn,р, если ξ принимает значения 0, 1, …,n с вероятностями P(ξ = k) = Cnk pk (1-p)n-k . Случайная величина ξ с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха р .
Таблица распределения ξ имеет вид
-
ξ
0
1
…
k
…
n
Р
(1-p)n
n p(1-p)n-1
…
Cnk pk (1-p)n-k
…
Pn
5. Как связаны биномиальное распределение и распределение Бернулли?
Сохраняются все предположения сделанные в схеме Бернулли. Дополняются тем что производится n – незав. испытаний, в каждом из которых вер. P одинакова.
В результате таких испытаний имеем:
СВ. ξ – число успехов в схеме Бернулли
6. Вычислить математическое ожидание случайной величины, имеющей биномиальное распределение.
1). ξ k – СВ. Бернулли
2). ξ k - независимые, одинаково распределенные.
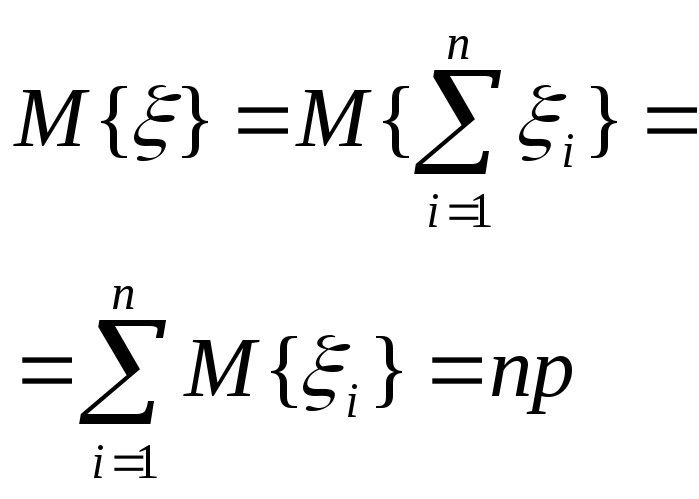
7. Вычислить дисперсию случайной величины, имеющей биномиальное распределение.
На основе выше сказанного условия
8. Дать определение распределения Пуассона.
Случайная
величина ξ
имеет распределение Пуассона с параметром
λ,
где λ
> 0 ,
и ξ
П
λ,
если ξ
принимает значения 0,
1, 2 …
с вероятностями. Где λ
– параметр
распределения Пуассона. Функция
распределения приближается к 1
асимптотически (
)
9. Вычислить математическое ожидание случайной величины, имеющей распределение Пуассона.
10. Записать формулу плотности вероятностей нормального распределения. Нарисовать ее график.
x∈(-∞;∞)
11. Записать формулу функции распределения нормального распределения. Нарисовать ее график.
12. Как определяется функция Лапласа? Нарисовать ее график.
dx
при х>5 F~0.5
13. Перечислить основные свойства функции Лапласа.
1. Функция Лапласа нечётная.
2. Функция Лапласа монотонно возрастающая.
3.
()=
0,σ
(-x)=- 
(x)
4.
(-)=
-0.5
5.
6.
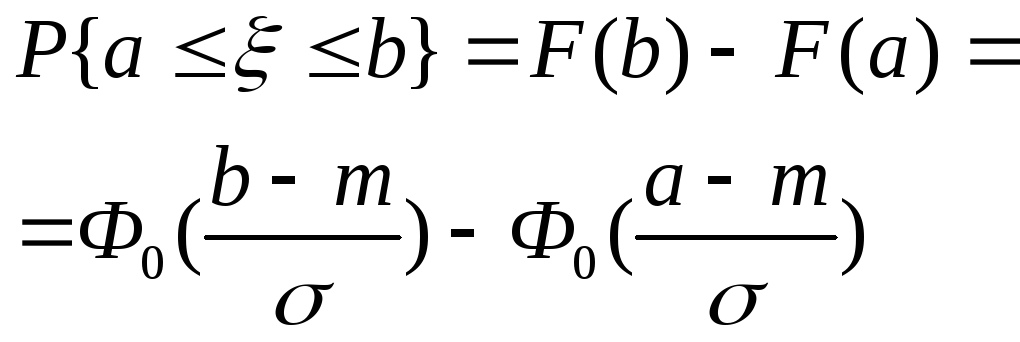
14. Выразить функцию распределения гауссовской случайной величины через функцию Лапласа.
15. Записать формулу для нахождения вероятности попадания гауссовской случайной величины в интервал [a; b].
.
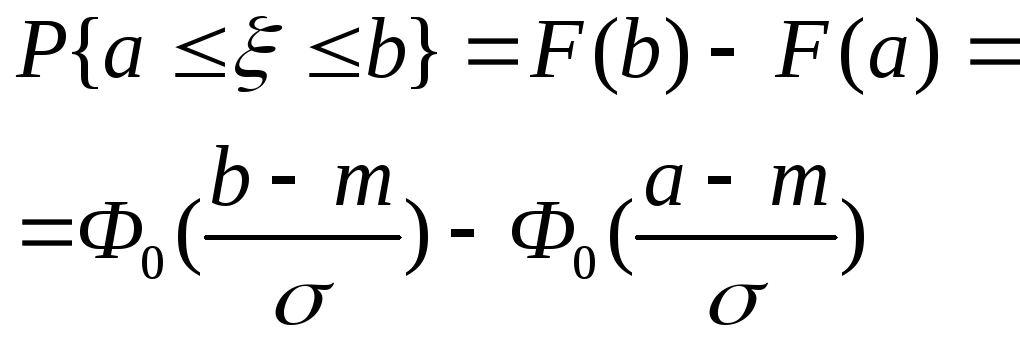
16. Сформулировать правило трех сигм.
Свероятностью фактически равной 1 значение нормальной СВ лежат в диапазоне m±3σ
17. Вычислить математическое ожидание случайной величины, имеющей нормальное распределение.
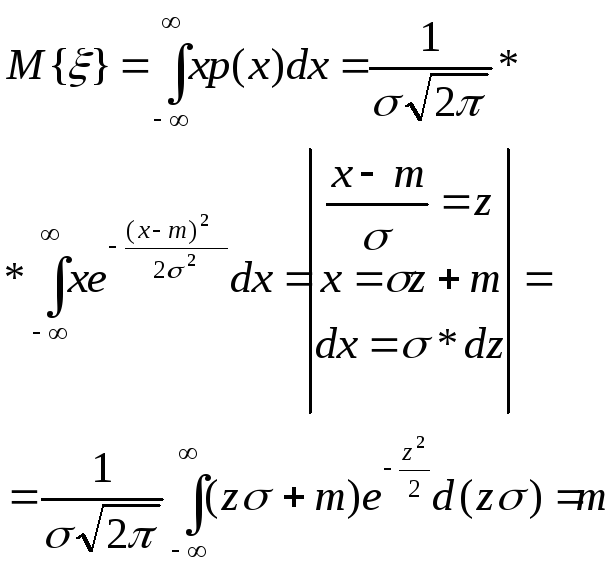
18. Записать формулу плотности вероятностей равномерного распределения. Нарисовать ее график.
19. Записать формулу функции распределения равномерного распределения. Нарисовать ее график.
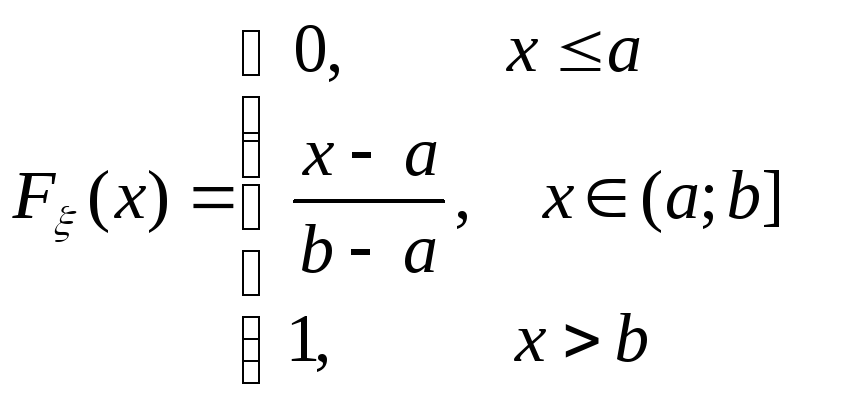
20. Вычислить математическое ожидание равномерного распределения.
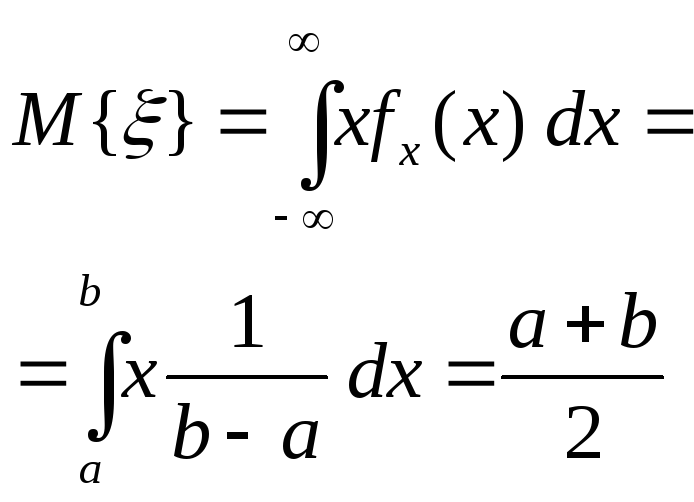
21. Чему равна дисперсия случайной величины с равномерным законом распределением?
22. Записать формулу плотности вероятностей показательного распределения. Нарисовать ее график.
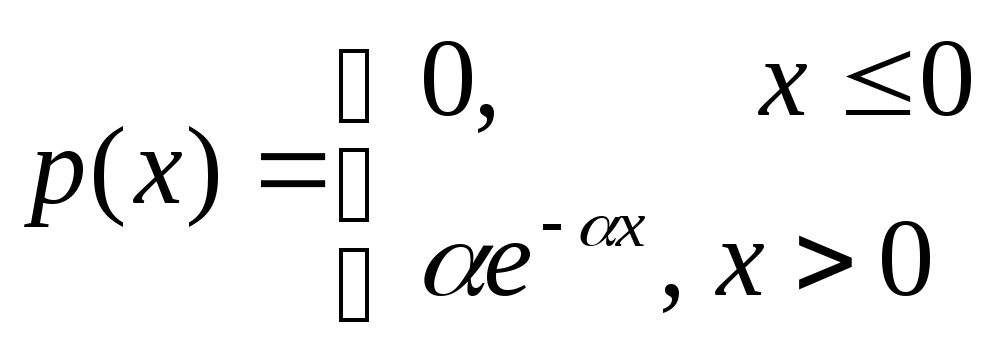
23. Записать формулу функции распределения показательного распределения. Нарисовать ее график.
24. Вычислить математическое ожидание случайной величины, имеющей показательное распределение.
Найдем для произвольного k N момент порядка k.
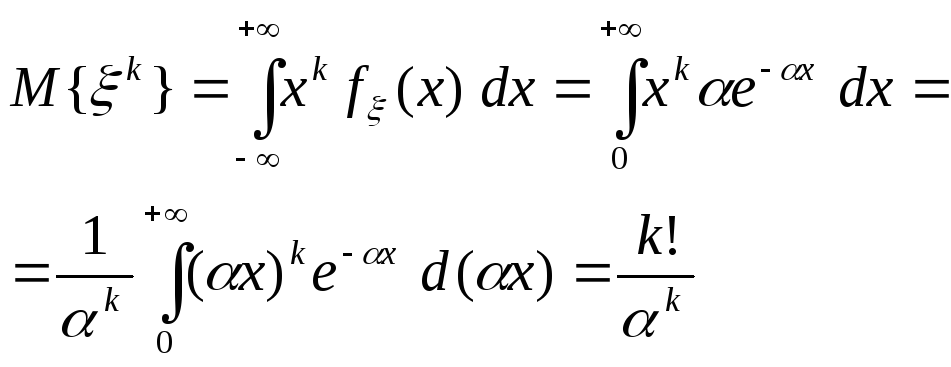
25. Чему равна дисперсия случайной величины, имеющей показательное распределение?
