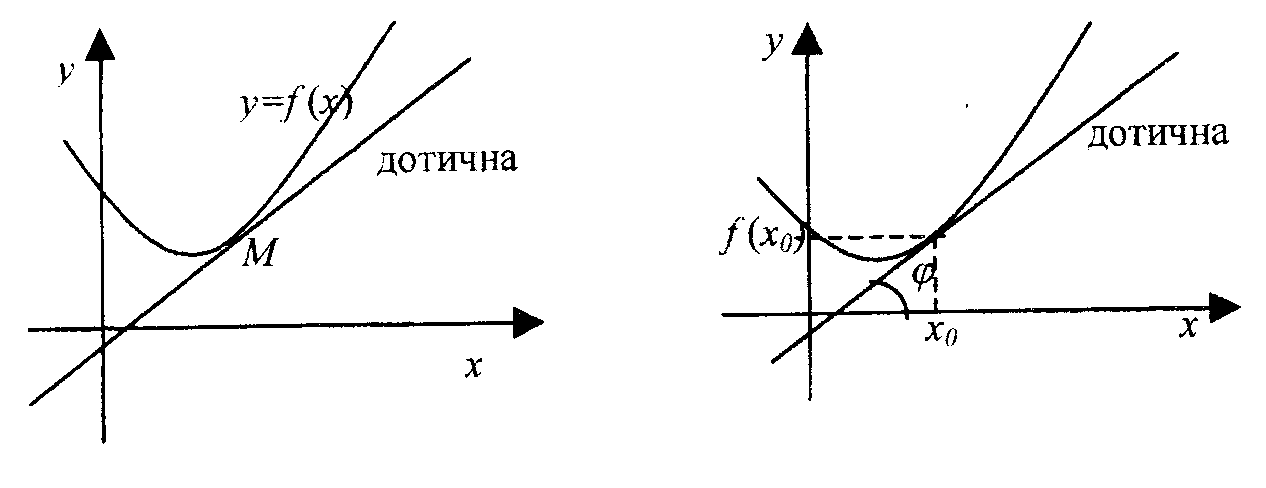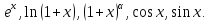Shpargalka2

22. Фундаментальні послідовності. Критерій Коші.

22. Фундаментальна послідовність. Коші.

Фундаментальна послідовність — в математичному аналізі послідовність, члени якої наближаються як завгодно близько один до одного зі збільшенням порядкових номерів.

Означення.

• Послідовність елементів метричного простору називається фундаментальною послідовністю, якщо для кожного дійсного існує таке ціле (яке залежить від ), що для всіх цілих виконується

(так званий критерій Коші).

Трохи неформально висловлюючись, вимагаємо, що члени послідовності із достатньо великими індексами (більшими за ) стають як завгодно близькими один до одного у (відстань менша за ). Це наштовхує на думку про існування границі фундаментальної послідовності у . Але насправді границі може й не бути! А саме,

• Метричний простір в якому кожна фундаментальна послідовність має границю в називають повним.

(Неформально: у "немає дірок", множина точок розриву є множина міри 0, М - вимірна за Жорданом.)

23. Границя функції в точці. Означення: за коші, за Гейне. Властивості.

Определим понятие окрестности точки х₀ как множество значений х, являющихся решениями неравенства 0<|x - x₀| < δ, где δ > 0 – некоторое число. Само значение х₀ может включаться в окрестность или не включаться в нее (в этом случае окрестность называется проколотой).

Пусть функция у = f(x) определена в некоторой окрестности точки х₀.

Определение 13.7. Число А называется пределом функции у = f(x) при х, стремящемся к х₀, если такое, что |f(x) - A| < ε при |x - x₀| < δ.

Обозначение: .

Замечание. Для существования предела функции в точке х₀ не требуется, чтобы функция была определена в самой этой точке.

Определение 13.8. Функция у = f(x) имеет бесконечный предел при х, стремящемуся к х₀ (стремится к бесконечности, является бесконечно большой), если такое, что |f(x)| > M при

|x - x₀| < δ.

Обозначение:

Определение 13.9. Число А называется пределом функции y = f(x) на бесконечности, если при x > X (), при x < -X (), при |x| > X (

Замечание. Бесконечный предел функции на бесконечности можно определить по аналогии с определением 13.8.

Определение 13.10. Функция у = f(x) называется ограниченной в некоторой области значений х, если существует число М>0 такое, что |f(x)|<M для всех значений х, принадлежащих рассматриваемой области.

24. Відношення «0»та «о». Властивості.

Рассмотрим функции α(х) и β(х), для которых то есть бесконечно малые в окрестности х₀.

1. Если то α(х) и β(х )называются бесконечно малыми одного порядка. В частности, если А=1, говорят, что α(х) и β(х) – эквивалентные бесконечно малые.

2. Если то α(х) называется бесконечно малой более высокого порядка по сравнению с β(х).

3. Если , то α(х) есть бесконечно малая порядка n по сравнению с β(х).

Обозначения: α(х)=О(β(х)) – бесконечно малые одного порядка, α(х)~β(х) – эквивалентные бесконечно малые, α(х)=о(β(х)) – α есть бесконечно малая более высокого порядка, чем β.

Замечание 1. Используя 1-й и 2-й замечательные пределы и их следствия, можно указать бесконечно малые функции при х→0, эквивалентные х: sinx, tgx, arcsinx, arctgx, ln(1+x), e^x-1.

Замечание 2. При раскрытии неопределенности вида , то есть предела отношения двух бесконечно малых, можно каждую из них заменять на эквивалентную – эта операция не влияет на существование и величину предела.

Пример.

25. Еквівалентні функції. Властивості. Порядок однієї функції відносно іншої. Шкала порівняння.

Якщо функція замінюється на де якому кроці через , то різницяь називається абсолютною похибкою, а відношення — відносною похибкою зробленої заміни. Якщо вивчається поведінка функції при то часто доцільно замінити її функцією такої, що 1) функція в певному значенні більш проста, ніж функція ; 2) абсолютна похибка прямує до нуля при

В цьому випадку говорять, що наближає функцію поблизу точки . Такою властивістю володіють наприклад, всі нескінченно малі при функції f і g. Нижче показано, що серед них лише ті, які еквівалентні між собою:

_{володіють тією властивістю, що не тільки абсолютна похибка} , але і відносна прямує до нуля при

В цьому значенні функції, еквівалентні заданій, наближають її краще, ніж інші функції навіть того ж порядку, що і дана при

Наприклад, функції є нескінченно малими при так само як і а тому абсолютні похибки при заміні sin кожна з них прямує до нуля при

Але лише одна зі всіх перерахованих функцій, а саме: має ту властивість, що відносна похибка при заміні цією функцією прямуватиме до нуля при

Прямування відносної похибки до нуля при можна записати, використовуючи символ “o мале»:

Сформулюємо сказану характеристичну властивість еквівалентних функцій у вигляді теореми.

Теорема 1. Для того, щоб функції і були еквівалентними при необхідно і достатньо, щоб при виконувалася умова

(1.32)

Теорема 2. Нехай ~ і ~ при Тоді якщо існує

(1.33)

то існує і , причому

(1.34)

26. Неперервні функції. Властивості. Теорема про існування та неперервність оберненої функції.

Функція називається неперервною в точці , якщо границя функції в точці дорівнює значенню функції в цій точці:

Приклад 12. Довести неперервність функції точці х = 3.

Розв'язання

;

Оскільки то задана функція неперервна в точці х=3, що і треба було довести.

Функція називається неперервною в точці ,якщо

• ) визначена в точці ,

• границя зліва в точці дорівнює границі справа в цій точці і дорівнює значенню в ній функції:

.

Функція неперервна на проміжку, якщо вона неперервна в кожній точці цього проміжку.

Функція неперервна на відрізку [a;b], якщо вона неперервна на проміжку (a;b) і неперервна в точці х = а справа і в точці х = b зліва.

27. Властивості неперервних функції на відрізку. Перша та друга теореми Вейєрштраса, теорема Коші.

Теорема (первая теорема Вейерштрасса)

Если функция непрерывна на сегменте, то она ограничена на нем.

Доказательство: методом от противного, воспользуемся свойством замкнутости сегмента [a;b]. Из любой последовательности (xn) этого сегмента можем выделить подпоследовательность xnk, сходящуюся к x0∈[a;b] .

Пусть f не ограничена на сегменте [a;b], например, сверху, тогда для всякого натуральногоn∈N найдется

точка xn∈[a;b] , что f(xn)>n. Придавая n значения 1,2,3,{\ldots}, мы получим последовательность (xn)

точек сегмента [a;b], для которых выполнено свойство f(x₁)>1,f(x₂)>2,f(x₃)>3,...,f(x_n)>n...

Последовательность (xn) ограничена и поэтому из нее по теореме можно выделить подпоследовательность(xnk), которая сходится к точке x0∈[a;b] : limk→∞x_nk=x₀ (1)

Рассмотрим соответствующую последовательность (f(x_nk)). С одной стороны f(x_nk)>_nk и поэтому limk→∞f(x_nk)=+∞

(2),

С другой стороны, учитывая определение непрерывной функции по Гейне из (1) будем иметь limk→∞f(x_nk)=f(x₀) (3)

Получаем равенства (2) и (3) противоречат теореме (о единственности предела). Это противоречие и доказывает справедливость теоремы. Аналогично доказывается ограниченность функции снизу. Ч.Т.Д.

Замечание 1

Таким образом, если f непрерывна на [a;b], то ее множество значений ограничено и поэтому существует конечные верхняя и нижняя грань функции.

c=infx∈[a;b]f(x),d=supx∈[a;b]f(x), но открыт вопрос о достижении

функции своих граней.

Замечание 2

Если слово сегмент в условии теоремы заменить словом интервал или полуинтервал, то теорема может и нарушиться. Пример, y=tgx,tgx∈C((−2π;2π)) , но функция не ограничена на этом интервале.

Теорема (вторая теорема Вейерштрасса)

Если функция непрерывна на сегменте, то она достигает на нем своих граней (т.е. непрерывная на сегменте функция принимает свое наибольшее и наименьшее значения).

Доказательство: Пусть f(x)∈C([a;b]) , c=infx∈[a;b]f(x), d=supx∈[a;b]f(x). По первой

теореме Вейерштрасса c,d∈R . Докажем, что f достигает на [a;b] своих граней, т.е. найдутся такие точки

x1,x2∈[a;b]

, что f(x1)=c,f(x2)=d.

Докажем, например, существование точки x2.

По определению верхней грани имеем (∀x∈[a;b])(f(x)=d) . Предположим противное, т.е. точки x2, в

которой f(x2)=dна [a;b], тогда на [a;b] выполняется условиеf(x)<d или d−f(x)>0 . Далее введем

вспомогательную функцию ϕ(x)=1d−f(x) .

ϕ(x) на [a;b] положительна и непрерывна (как отношение двух

непрерывных на [a;b] функций и d−f(x)/=0) , поэтому по первой Т. Вейерштрасса

ϕ(x) на [a;b] ограничена.

Это означает, что при некотором М>0 (∀x∈[a;b])(0<1d−f(x)≤M) , отсюда имеем

f(x)≤d−1M<d .

28. Розриви функцій, класифікація точок розриву. Рівномірна неперервність, теорема Кантора.

Функція , яка не є неперервною в точці назива­ється розривною в цій точці. Точка називається точкою роз­риву першого роду функції , якщо існують скінчені од­носторонні границі , і при цьому:

• - неусувний розрив першого роду;

• - усувний розрив першого роду.

Точка називається точкою розриву другого роду фун­кції , якщо одна із односторонніх границь , не існує або нескінченна.

3.2.11. Методика дослідження функції на неперервність

1. Знаходимо точку - "підозрілу" на розрив.

Це може бути точка, в якій функція невизначена або змі­нює закон визначеності.

2. Визначаємо інтервали неперервності функції.

3. Обчислюємо , .

4. Робимо висновок згідно з теоремами, або вико­ристовуючи означення точок розриву.

Числова функція речового змінного рівномірно неперервна, якщо

Тут важливо, що вибір залежить тільки від величини .

Теорема Кантора — Гейне в математичному і функціональному аналізі стверджує, що функція, неперервна на компакті, рівномірно неперервна на ньому.

Нехай дано два метричних простори і Нехай також дано компактну підмножину і визначено на ній неперервну функцію Тоді рівномірно неперервна на .

29. Поняття похідної. Фізична та геометрична інтерпретації. Правила обчислення похідних. Похідні елементарних функцій.

Похідною функції в точці називається границя відношення приросту функції до приросту аргументу, коли при­ріст аргументу прямує до нуля, тобто, де - позначення похідної, запропоноване Ньютоном;

; - позначення Лейбніца похідної функції

Операція шукання похідної називається диференціюванням. Функція називається диференційованою в точці о, якщо існує похідна цієї функції в цій точці.

Дотичною до кривої в даній точці М називається гра­ничне положення січної MN, коли точка N наближається вздовж кривої до точки М,

Значення похідної в точці дорівнює кутовому коефіцієнту дотичної до графіка функції в точці і дорівнює тангенсу кута нахилу дотичної до додатного напряму осі ОХ:

де - кутовий коефіцієнт дотичної до графіка функції.

- рівняння дотичної до графіка функції в точці з абсцисою

Фізичний зміст похідної

Якщо ) - залежність пройденого шляху від часу, то:

1. - швидкість прямолінійного руху;

2. прискорення прямолінійного руху.

1. Похідна алгебраїчної суми двох диференційованих функцій дорівнює відповідній алгебраїчній сумі похідних цих функцій: .

Полученное неравенство противоречит тому, что d является верхней гранью функции f(x) на [a;b], т.е. наименьшим из верхних границ. Полученное противоречие и означает существование точки x2 такой, что f(x2)=d.

Аналогично доказывается существование точки x1∈[a;b] , такой что f(x1)=c.

Следствие

Если f непрерывна и непостоянна на [a;b], то образ этого отрезка [a;b] при отображении f будет так же отрезок, т.е. непрерывный непостоянный образ отрезка есть отрезок.

Доказательство: В самом деле образом отрезка [a;b] при отображении f будет отрезок [с;d], где c=inf[a;b]f(x)=min[a;b]f(x), а d=sup[a;b]f(x)=max[a;b]f(x), что следует из второй теоремы Больцано-Коши и второй теоремы Вейерштрасса Ч.Т.Д.

Теорема (первая теорема Больцано-Коши) Если функция непрерывна на I и в 2 его точках a и bпринимает значения разных знаков, то по крайней мере в одной точке c между a и b функция обращается в нуль, т.е. f(c)=0

Геометрический смысл: График непрерывной на промежутке и принимающей в двух точках этого промежутка значения разных знаков пересекает ось абсцисс по крайней мере в одной точке.

f(a)<0,f(b)>0,f(c)=0

В теореме лишь утверждается существование нуля функции такой точки c, гдеf(c)=0, но не показывает метода нахождения точки.

Замечание. Доказанная теорема играет важную роль и при решении неравенств.

Теорема (вторая теорема Больцано - Коши) Если f непрерывна на I и в двух его точках a и bf(a)=A>B=f(b), то для всякой точки C∈[B,A] между точками a и b найдется хотя бы одна точкаc,

чтоf(c)=C.

Геометрический смысл этой теоремы: всякая прямаяy=C, где B<C<A, пересечет график функции f по крайней мере в одной точке.

Замечание. Если f - непрерывна и непостоянна на I, то образом этого промежутка I при отображении f будет также промежуток (т.е. непрерывным образ f(I)промежутка I есть промежуток). В самом деле, по теореме из того, что B,A∈E(f) следует, что интервал

(B;A)⊂E(f) , т.е.

E(f)⊂f(I) - промежуток.

2. Похідна добутку двох диференційованих функцій до­рівнює сумі добутків похідної першої функції на другу функцію і першої функції на похідну другої функції:

3. Сталий множник можна винести за знак похідної:

де С - константа (число).

4. Похідна частки двох диференційованих функцій дорівнює дробу, знаменником якого є квадрат знаменника цього дробу, а чисельником - різниця між добутком похідної чисель­ника на знаменник і добутком чисельника на похідну знаменни­ка: .

5. Похідна складеної функції дорівнює добутку похідної функції за проміжним аргументом u на похідну проміжного аргументу за х. Якщо , то

1. , с - стала

2. . ,

3. .

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

30. Теореми Ролля, Лангранжа, Коші.

Теорема Ролля. Нехай задано функцію , непере­рвну на відрізку [а,b] і диференційовну на інтервалі (а,b). Тоді, якщо f(a) = f(b), то всередині відрізка [а, b] знайдеться точка С(а<С<b), така що .

Геометрична інтерпретація теореми Ролля: якщо виконуються умови тео­реми Ролля, то знайдеться хоча б одна точка С, в якій дотична паралельна осі абсцис. У цій точці похідна й дорівнює нулю.

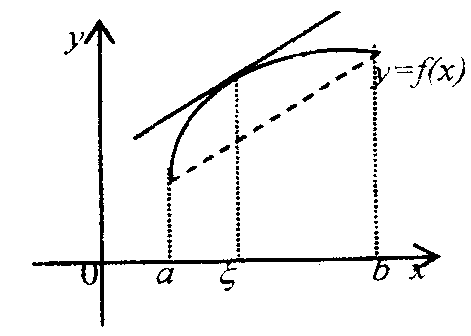
Теорема Лагранжа (про скінченні прирости функції). Нехай задано функцію y-f(x), неперервну на відрізку [а,b] і диференційовану на інтервалі (а, b). Тоді знайдеться точка (а<<b), така що похідна функції в цій точці дорівнюватиме відношенню , тобто

Геометрична інтерпретація тео­реми Лагранжа: на інтервалі знайдеться хоча б одна точка , в якій дотична є паралельною хорді, що сполучає кінці дуги функції f(x) на відрізку [а,b].

Теорема Коші (пpo кінцеві прирости двох функцій). Не­хай на відрізку [а,b] задано дві функції і . Якщо ці фун­кції неперервні на відрізку [а, b] і диференційовані на інтервалі (а,b), причому , то на інтервалі (а,b) існує точка так що .

Геометрична інтерпретація теореми Коші. Нехай рівняння (4.1)

є рівнянням кривої, де на функції і накладено умови теореми Коші. Теорема Коші ствер­джує існування точки , в якій дотична до кривої (4.1) парале­льна хорді, що сполучає кінці цієї кривої.

31. Диференціал, похідні та диференціали старших порядків. Формула Лейбниця

Похідною другого порядку функції в точці х нази­вається похідна від функції (похідна від похідної першого порядку цієї функції), тобто

Позначення похідної другого порядку: .

Приклад 4. Знайти похідну другого порядку функції

Розв’язання:

.

Відповідь: .

Похідною n-го порядку функцій називається похідна функції (похідна від похідної (n-1)-го порядку),

Позначення похідної n-ro порядку:

Приклад 5. Знайти похідну 3-го порядку функції .

Розв’язання

, .

Відповідь: 0.

4.2. Диференціали вищих порядків

Диференціалом 2-го порядку функції в точці х називається вираз (диференціал від диференціала 1-го порядку функції в цій точці). .

32. Формула Тейлора для многочлена. Формула Тейлора із залишковим членом у формі Пеано, Лангранжа.

Формула Тейлора

33. Формула Маклорена для

Формула Маклорена

Экспонента :

Натуральный логарифм:

Биномиальное разложение

для всех и всех комплексных где

Диференціалом n-го порядку функції в точці x називається вираз (диференціал від диференціала (n-l)-ro порядку функції в цій точці)

Приклад 6. Знайти диференціал 3-го порядку функції

Розв'язання

Диференціал 3-го порядку функції знайдемо за формулою

.

Отже, .

Відповідь: .

4.3. Правила знаходження диференціала

1. Диференціал суми двох диференційовних функцій u і v дорівнює сумі диференціалів цих функцій: .

2. Диференціал добутку двох диференційовних функцій u і v визначається за формулою .

3. Диференціал частки двох диференційовних функцій u і v визначається за формулою .

4. Диференціал складеної функції. Нехай , тобто .

Тоді .

; - позначення Лейбніца похідної функції

34. Правило Лопіталя.

Нехай функції і :

1) диференційовні в деякому околі точки а і в цьому околі ;

2) одночасно є нескінченно малими або нескінченно великими в точці а;

3) існує границя відношення похідних цих функцій

Тоді існує границя відношення цих функцій причому =

Приклад 1. За правилом Лопіталя знайти .

.

Відповідь: .

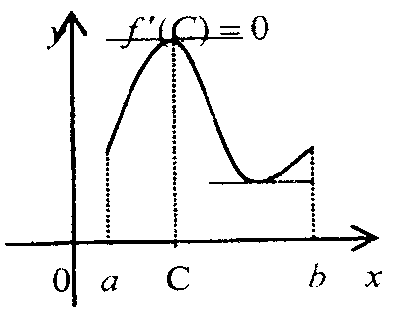
35. Дослідження функцій за допомогою похідних: умови локального екстремуму, опуклість і точки перегину, асимптоти.

Точки максимуму і точки мінімуму назива­ються точками екстремуму. Значення функції в точках макси­муму та мінімуму називається екстремумами (мак­симумом і мінімумом) функції.

Критичні точки - це внутрішні точки області визначення функції, в яких похідна функції дорівнює нулю або не існує.

Необхідна умова екстремуму

Точка є точкою екстремуму функції , якщо похідна функції в цій точці дорівнює нулю або не існує .

- точка екстремуму

Достатня умова екстремуму.

Якщо функція неперервна в точці і похідна функції змінює знак в цій точці, то - точка екстремуму функції

у точці знак змінюється з „+” на „-” - точка максимуму

у точці знак змінюється з „-” на „ +” - точка мінімуму

Алгоритм дослідження функції на зростання (спадання) та екстремуми.

1. Знайти область визначення та інтервали, на яких функція неперервна.

Знайти похідну .

Знайти критичні точки: а)

б) не існує.

4. Позначити критичні точки на області визначення функції, розбити цими точками область визначення на інтервали. Знайти знак похідної на кожному інтервалі.

5. Знайти проміжки зростання (>0) та проміжки спадання (< 0).

6. Визначити точки екстремуму і . Знайти і .

36. Невизначений інтеграл. Елементарні властивості, таблиця

2. Невизначений інтеграл. Задача інтегрування

Означення: Операція знаходження первісних для ф-ії f(x) називається інтегруванням.

Задача інтегрування функції на проміжку полягає в тому, щоб знайти всі первісні функції на цьому проміжку. Для розв’язання задачі інтегрування функції достатньо знайти одну будь-яку первісну на розглядуваному проміжку, наприклад F(x), тоді (за теоремою про множину первісних) F(x)+С – загальний вигляд всієї множини первісних на цьому проміжку.

Означення: Ф-ія F(x)+С, зо являє собою загальний вигляд всієї множини первісних для ф-ії f(x) на проміжку І і позначається

де ­f(x) – підінтегральна ф-ія; f(x)dx – підінтегральний вираз; dx – диференціал змінної інтегрування.

Теорема Коші. Для існування невизначеного інтеграла для ф-ії f(x) на певному проміжку достатньо, щоб ­f(x) була неперервною на цьому проміжку.

Неінтегровні інтеграли – які неможливо записати через основні елементарні ф-ії.

3. Властивості невизначеного інтеграла

Властивості, що випливають із означення невизн. інт:

І. похідна від невизначеного інтеграла дорівнює підінтегральній ф-ії:

ІІ. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу.

ІІІ.

Властивості, що відображають основні правила інтегрування:

IV. Сталий множник, що не дорівнює нулю, можна виносити з-під знака інтеграла.

V. Невизн. інтеграл від суми функцій дорівнює сумі невизначених інтегралів від цих функцій, якщо вони існують.

37. Інтегрування за допомогою підстановки та частинами

5. Інтегрування частинами

Теорема: Якщо функції u(x) та v(x) мають неперервні похідні, то:

На практиці ф-ії u(x) та v(x) рекомендується вибирати за таким правилом: при інтегруванні частинами підінтегральний вираз f(x)dx розбивають на два множники типу udv, тобто f(x)dx=udv; при цьому ф-ія u(x) вибирається такою, щоб при диференціюванні вона спрощувалася, а за dv приймають залишок підінтегрального виразу, який мітить dx, інтеграл від якого відомий, або може бути просто знайдений.

Деякі типи інтегралів і їх заміни:

v(x):

де Р(х) – многочлен, Q(x) – алгебраїчна ф-ія.

6. Метод підстановки

Мета – перетворити інтеграл до такого вигляду, який простіше інтегрувати.

Теорема. Якщо f(x) – неперервна, а x=(t) має неперервну похідну, то:

Наслідок.

7. Метод безпосереднього інтегрування

В цьому методі використ. формула

варіанту заміни змінної, але саму змінну не записують (роблять усно) При цьому використовують операцію внесення ф-ії під знак диференціала.

Через це, якщо: , то:

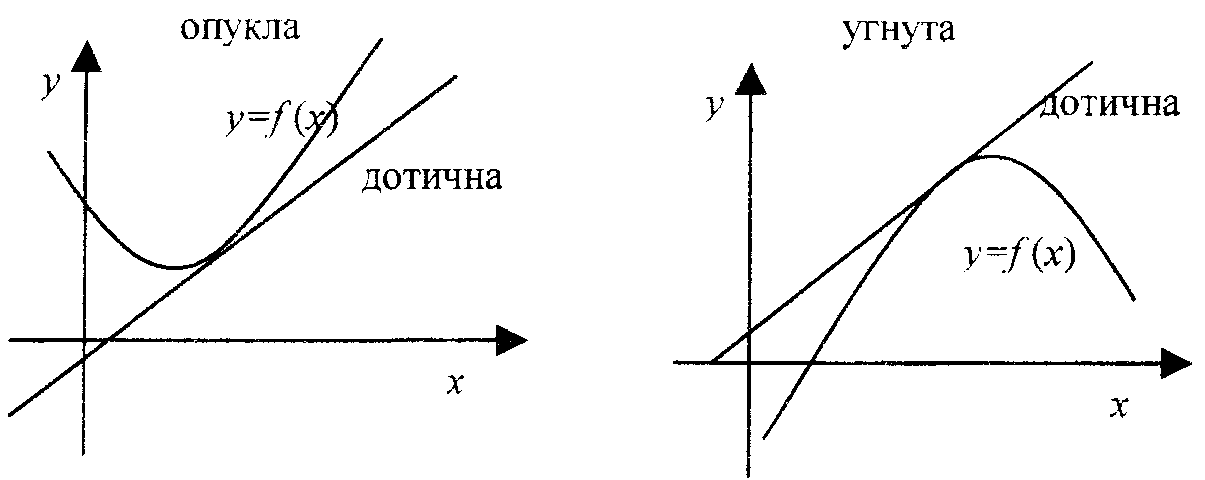
Крива називається опуклою на інтервалі (а,b), якщо всі її точки, крім точки дотику, лежать вище довільної її дотичної на цьому інтервалі.

Крива називається угнутою на інтервалі (а,b), якщо всі її точки, крім точки дотику, лежать нижче довільної її дотичної на цьому інтервалі.

Точка кривої називається точкою її перегину, якщо вона відділяє її опуклу частину від угнутої.

Достатні умови опуклості на угнутості функції

Якщо в кожній точці інтервалу (a,b) і то на інтервалі (а,b) графік функції напрямлено опуклістю вниз (опук­лий).

Якщо в кожній точці інтервалу (a,b) , то на інтервалі (а,b) графік напрямлено опуклістю вгору (угнутий).

Необхідна умова існування точки перегину

У точках перегину функції її друга похідна дорівнює нулю або не існує.

Алгоритм дослідження функції на опуклість, угнутість і точки перегину

1. Знайти область визначення і інтервали, на яких функ­ція неперервна.

2. Знайти другу похідну

3. Знайти внутрішні точки області визначення, в яких або не існує.

4. Позначити одержані точки на області визначення, знайти знак другої похідної функції на кожному інтервалі, на які розвивається область визначення.

5. Записати потрібний результат дослідження (інтервали опуклості, угнутості і точки перегину).

Пряма L називається асимптотою кривої, якщо відстань б від змінної точки М кривої до цієї прямої прямує до нуля, коли точка М, рухаючись по кривій, віддаляється на нескінченність.

Пряма х=а називається вертикальною асимптотою кривої y=f(x) , якщо при хоча б одна з односторонніх границь функції f(x) була нескінченною. Таким чином, вертикальна асимптота х = а існує тільки тоді, коли в точці х = а функція f(x) має нескінченний розрив.

38. Інтегрування раціональних функцій (інтегрування елементарних дробів)

Означення: Відношення двох многочленівназивається раціональним дробом.

Означення: Раціональний дріб правильний, якщо степінь многочлена в чисельнику менший степеня многочлена в знаменнику, тобто n<m. Якщо ж nm, то дріб неправильний.

Найпростіші раціональні дроби (4 типи):

1. 2. 3. 4.

де k2, kN, D=p²-4q<0

Теорема: Будь-який правильний раціональний нескоротний дріб можна представити у вигляді скінченого числа найпростіших дробів використовуючи такі правила:

1) Якщо Q_m(x)=(x-a)^kg_m-k(x), то:

2) Якщо Q_m(x)=(x²+px+q)^kg_m-2k(x), то:

де А_і, В_і, – деякі коефіцієнти, та правильні раціональні дроби.

Методика інтегрування раціональних ф-ій:

1. Якщо підінтегральна ф-ія – неправильний раціональний дріб, то за допомогою ділення його розкладають на суму многочлена і правильного раціонального дробу.

2. Знаменник правильного раціон. дробу розкладають на множники. По вигляду знаменника, правильний раціон. дріб представляють у вигляді найпростіших дробів, використовуючи метод невизначених коефіцієнтів.

3. Інтегрують цілу частину і найпростіші дроби.

39. Інтегрування тригонометричних виразів.

9. Інтегрування тригонометричних функцій

Розглянемо R(sin x,cos x)dx, де R – раціональна ф-ія відносно sin, cos, тобто над sin, cos викон. лише арифметичні дії та піднесення до цілого степеня. Існують такі підстановки, що за їх допомогою інтеграл R(sinx,cosx)dx завжди може бути зведений до інтеграла від раціональної ф-ії R*(t)dt, загальна схема інтегрування якої розроблена.

1) Універсальна тригонометрична підстановка . На практиці універсальну тригонометричну підстановку використовують, якщо sin x, cos x входять в невисокому степені, інакше підрахунки будуть складні.

2) Підінтегральна ф-ія – непарна відносно sin x, тоді роблять підстановку cos x = t.

3) Підінтегральна ф-ія – непарна відносно cos x раціоналізується за допомогою підстановки sin x = t.

4) Підінтегральна ф-ія R(sin x, cos x) – парна по sinx, cosx сукупно, тобто R(-sinx,-cosx)=R(sinx,cosx). В цьому випадку використовують підстановку tgx=t або ctgx=t.

5) Підінтегральна ф-ія R(tgx) раціоналізується підстановкою tgx=t.

В інтегралах sin²ⁿxcos^2mxdx рекомендується скористатися формулами зниження степеня.

40. Інтегрування ірраціональних функцій.

10. Інтегрування ірраціональних функцій.

1)

2)

3)

Підінтегральна ф-ія після виділення повного квадрата і заміни раціоналізується тригонометричними підстановками.

41. Інтегрування біноміальних диференціалів.

42. Визначений інтеграл. Означення, властивості. Умови інтегрованості функцій. Теорема про середнє

1. Поняття визначеного інтеграла

Означення: Якщо існує скінченна границя інтегральних сум S_n при _і­­0 і не залежить ні від способу розбиття [a;b] на частини х_і, ні від вибору точок _і, то ця границя називається визначеним інтегралом від ф-ії f(x) на проміжку [a;b] і позначається:

За означенням, визначений інтеграл – число, яке залежить від типу ф-ії f(x) та проміжку [a;b]; він не залежить від того, якою буквою позначена змінна інтегрування.

Ф-ія, для якої на інтервалі існує визначений інтеграл називається інтегровною.

2. Властивості визначеного інтеграла

1) Якщо f(x)=c=const, то

2) Сталий множник можна виносити з-під знака визначеного інтеграла.

3) Якщо f₁(x) та f₂(x) інтегровні на [a;b], то:

4) Якщо у визначеному інтегралі поміняти місцями межі інтегрування, то інтеграл лише змінить свій знак на протилежний.

5) Визначений інтеграл з однаковими межами інтегрування дорівнює нулю.

6) Якщо f(x) – інтегровна в будь-якому із проміжків [a;b], [a;c], [c;b], то:

7) Якщо f(x)0 і інтегровна для x[a,b], b>a, то

8) Якщо f(x), g(x) – інтегровні та f(x)g(x) для x[a;b], b>a, то:

43. Похідна інтеграла зі змінною верхньою межею. Формула Ньютона-Лейбниця. Зміна змінної.

Теорема: Якщо ф-ія f(x) неперервна для будь-якого x[a;b], то похідна від інтеграла із змінною верхньою межею інтегрування по цій межі дорівнює підінтегральній ф-ії від верхньої межі інтегрування, тобто:

Наслідки: 1) Визначений інтеграл із змінною верхньою межею від ф-ії f(x) є одна із первісних для f(x). 2) Будь-яка неперервна ф-ія на проміжку [a;b] має на цьому проміжку первісну, яку, наприклад, завжди можна побудувати у вигляді визначеного інтеграла із змінною верхньою межею.

Теорема (Ньютона-Лейбніца): Якщо ф-ія f(x) – неперервна для x [a;b], то визначений інтеграл від ф-ії f(x) на проміжку [a;b] дорівнює приросту первісної ф-ії f(x) на цьому проміжку, тобто:

де F’(x)=f(x)

Зв’язок між визначеним та невизначеним інтегралами можна представити такою рівністю:

Наслідок: Для обчислення визначеного інтеграла достатньо знайти одну із первісних підінтегральної ф-ії і виконати над нею подвійну підстановку.

4. Метод підстановки у визначеному інтегралі

Теорема: Якщо: 1) f(x) – неперервна для x[a;b]; 2) ()=а, ()=b; 3) x=(t) та ‘(t) – неперервні для t [;]; 4) при t [;]x [a;b], то

Зауваження: При заміні змінної інтегрування у визначеному інтегралі змінюються межі інтегрування і тому нема потреби повертатись до початкової змінної.

44. Площі плоских фігур.

Визначений інтеграл від додатної неперервної функції , заданої на відрізку , чисельно дорівнює площі криволінійної трапеції, обмеженої графіком функції і прямими (рис. 3.1):

. (3.1)

В разі, коли на (рис.3.2)

. (3.2

Якщо функція на відрізку скінчене число разів змінює знак, то

.

Площу фігури, обмеженої кривими та і прямими за умови, що (рис.3.3) знаходять за формулою

. (3.3)

45. Обчислення об’ємів тіл, тіл обертання.

Нехай функція - неперервна і додатна на відрізку .

Об’єм тіла, яке утворюється при обертанні навколо осі криволінійної

трапеції, обмеженої кривою та відрізками прямих (рис.3.6), дорівнює

. (3.11)

Якщо задані дві неперервні криві такі, що , при , то об’єм тіла, отриманого обертанням навколо осі плоскої фігури, обмеженої цими лініями та відрізками прямих (рис.3.7), обчислюється за формулою

. (3.12)

9) Якщо f(x) – інтегровна та mf(x)M, для x[a;b], b>a, то

10) (Теорема про середнє): Якщо ф-ія f(x) – неперервна для x[a;b], b>a, то знайдеться така точка x= c [a;b], що:

Об’єм тіла, утвореного обертанням навколо осі криволінійної трапеції, обмеженої неперервною кривою , прямою та відрізками прямих , (рис.3.8), дорівнює

. (3.13)

У разі параметричного задання кривої рівняннями , , об’єми утворених тіл обертання навколо осі або осі визначаються відповідно формулами:

, (3.14) . (3.15)

У випадку, коли фігура обмежена кривою та прямими (рис.3.4), її площу знаходять за формулою

. (3.4)

Якщо крива задана параметричними рівняннями , де - неперервні функції, що мають неперервні похідні на відрізку , то площа криволінійної трапеції, обмеженої цією кривою, прямими та відрізком осі , визначається за формулою:

, (3.5)

де і - значення параметра , при яких .

46. Обчислення довжини кривої.

Нехай крива задана рівнянням , , причому неперервна разом із своєю похідною на . Тоді довжина дуги кривої визначається формулою

. (3.7)

Вираз називається диференціалом дуги. В разі, коли крива задається рівнянням довжина дуги кривої обчислюється так:

. (3.8)

У разі параметричного задання кривої , довжина дуги дорівнює:

. (3.9)

Якщо ж гладка крива задана рівнянням в полярних координатах, то

. (3.10)

47. Площа поверхні обертання. Фізичні застосування.

Площа поверхні, утвореної обертанням навколо осі дуги гладкої кривої, заданої функцією , , обчислюється за формулою

. (3.17)

Якщо гладка крива задана рівнянням , , то площа поверхні, утвореної обертанням кривої навколо осі , може бути обчислена за формулою

. (3.18)

У разі параметричного задання кривої рівняннями , , , де функції , - неперервні

разом із своїми похідними, відповідні площі поверхні обчислюються за формулами:

, (3.19)

. (3.20)

Площа поверхні, отриманої обертанням навколо полярної осі криволінійного сектора, обмеженого неперервною кривою та двома полярними радіусами , , визначається за формулою

. (3.21)

Знайти площу поверхні сфери, як тіла обертання.

Розв’язання

Нехай сфера утворена обертанням кола навколо осі . Знайдемо :

(верхня половина кола), тоді

.

Обчислимо , тоді

.

Отже, за формулою (3.17):

.

Площа поверхні сфери дорівнює .