1. Расчет основных показателей динамики.

Анализ динамических рядов социально-экономических явлений обычно начинают с рассмотрения статистик, расчет которых не требует какой-либо предварительной обработки анализируемого динамического ряда. Речь идет о так называемых показателях динамического ряда, позволяющих пояснить характер, скорость, интенсивность и направление развития изучаемого явления за определенный временной период.

В результате того или иного сопоставления уровней динамического ряда формируется система абсолютных и относительных показателей динамики, к числу которых относятся абсолютные приросты (и их среднее значение), ускорение, коэффициенты роста (и их среднее значение), коэффициенты прироста (и их среднее значение), абсолютное значение одного процента прироста. Сравниваемый уровень динамического ряда называется текущим, а уровень, с которым производится сравнение, базисным. В зависимости от того, что принимается за базу сравнения будут получены различные показатели динамики. Приняв за базу сравнения некоторый постоянный уровень, например y1 получим серию базисных показателей, которые характеризуют окончательный результат всех изменений в уровнях ряда от первого периода (или момента времени) до текущего периода. Следует иметь ввиду, что в реальных задачах за базу сравнения может быть принят уровень ряда, относящийся к периоду (моменту), выходящему за пределы анализируемого динамического ряда (например, начальный момент периода с которого начинается некоторый новый этап развития).

Если производится сравнение текущего уровня (yt) с непосредственно предшествующим (yt-1), то получаются цепные показатели динамики. Для того, чтобы рассчитать цепные показатели динамики, необходимо построить временной ряд, опережающий исходный на один лаг.

Абсолютным приростом называется разность последующего и предыдущего уровней ряда динамики:

где y_i — текущий уровень ряда динамики;

y_i-1 — предыдущий уровень;

_i — абсолютный прирост.

За весь период, описываемый рядом, абсолютный прирост выразится как разность между последним уровнем ряда и первым его уровнем:

где y_n — последний уровень ряда;

у₁ — первый уровень.

Абсолютные приросты можно исчислить как накопленные итоги с начала исследуемого периода:

_iб = y_i – y₁

Абсолютный прирост может иметь положительный или отрицательный знак. Он показывает, насколько уровень текущего периода выше или ниже базисного.

Темпом роста называется отношение последующего уровня к предыдущему или какому-либо другому, принятому за базу сравнения. При помощи темпов роста измеряется, во сколько раз уровень текущего периода выше или ниже уровня базисного периода, или сколько процентов он составляет по отношению к базисному. Таким образом, темп роста может быть выражен в виде коэффициентов, когда определяется непосредственное отношение абсолютных размеров уровней, и в процентах, когда он показывает, сколько процентов текущий уровень составляет по отношению к базисному, принятому за 100%.

Темп роста в виде коэффициентов вычисляется по формулам:

 цепные темпы роста;

 базисные темпы роста;

-- темп роста за весь период.

T_p — темп роста.

Для выражения темпа роста в процентах достаточно его величину, выраженную в виде коэффициента, умножить на 100.

Величина темпа роста, большая единицы, показывает увеличение уровня текущего периода по сравнению с базисным. Величина темпа роста, равная единице, показывает, что уровень текущего периода по сравнению с базисным не изменился, а величина темпа роста, меньшая единицы, показывает уменьшение уровня текущего периода, но темп роста всегда имеет положительный знак.

Темпом прироста называется отношение абсолютного прироста к базисному уровню, т. е.

,

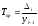где _i — абсолютный прирост данного уровня;

y_i-1 — базисный уровень (уровень предыдущего периода);

T_np — темп прироста (в виде коэффициента).

Темп прироста, выраженный в процентах, показывает, на сколько процентов увеличился или уменьшился текущий уровень по сравнению с базисным, принятым за 100%, или, иначе, сколько процентов составляет абсолютный прирост данного уровня по отношению к базисному.

Следующая статистическая характеристика динамики, основанная на измерении соотношений уровней, называется абсолютным значением одного процента прироста.

Абсолютное значение одного процента прироста показывает, какая абсолютная величина скрывается за относительным показателем — одним процентом прироста. Оно представляет собой отношение абсолютного прироста к темпу прироста, выраженному в процентах.

А так как темп прироста равен частному от деления абсолютного прироста, умноженного на 100, на величину первоначального уровня, то абсолютное значение 1% прироста оказывается равным первоначальному уровню, деленному на 100 (а = 0,01 y_i-1 )

Средний уровень ряда называемый также хронологической средней или временной средней. Средний уровень ряда рассчитывается по-разному для моментных и интервальных рядов динамики.

Чтобы найти средний уровень интервального ряда, достаточно сумму уровней этого ряда разделить на число периодов, к которым она относится, т. е.

.

Следовательно, средняя хронологическая интервального ряда динамики вычисляется по формуле средней арифметической простой.

В общем виде средний уровень моментного ряда можно определить по формуле

.

Средний абсолютный прирост есть средняя из абсолютных приростов за равные промежутки времени одного периода.

Если абсолютные годовые приросты обозначить через ₁, ₂, ₃, ... , то средний абсолютный прирост, обозначаемый через , может быть найден по формуле

,

где п—1 — число абсолютных приростов за период. Так как _i равна разности между последним и первым уровнем у_п—у₁, то средний абсолютный прирост можно найти по формуле:

.

Число абсолютных приростов меньше числа уровней на единицу.

При исчислении среднего темпа роста нужно учитывать, что скорость развития явлений идет по правилам сложных процентов, где накапливается прирост на прирост. Поэтому средний темп роста принято вычислять по формуле средней геометрической из темпов роста за составляющие период промежутки времени.

Если через T_p1, T_p2, T_p3, ... , Т_р обозначить темпы роста за равные промежутки, то средний темп роста выразится формулой:

,

где Т_р — средний темп роста;

n — число темпов.

Поскольку всякий темп роста является отношением уровней динамического ряда, так что; , ... , в формуле средней геометрической темпы роста заменяют соответствующим отношением уровней. Но так как число темпов роста на единицу меньше числа уровней, показатель корня должен быть равен числу уровней минус единица. Заменив темпы роста выражающими их отношениями и учитывая, что эти величины перемножаются, найдем подкоренное выражение как

.

Следовательно, средний темп роста может быть выражен формулой

,

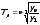где п — число уровней;

у_п  уровень последнего года (периода);

у₁ — уровень первого года (периода).

Абсолютный прирост второго порядка или прирост приростов определяется как разность приростов:

_i (2) =_i - _i-1

Результаты расчетов показателей по динамическим рядам представлены в таблицах 2, 3 . Как видно из таблицы практически для всех показателей все значения начинаются со второго уровня.

Таблица 2

Результаты расчетов основных показателей по импорту

год	Imports	базисный абсолютный прирост, млрд. доллларов США	цепной абсолютный прирост, млрд. долларов США		базисный темп роста, %		цепной темп роста,%		темп прироста,%		абсолютное значение одного процента прироста, млрд. долларов США
1977 год	153,602	-	-		-		-		-		-
1978 год	185,256	31,654	31,654		120,61%		120,61%		20,61%		1,536
1979 год	245,723	92,121	60,467		159,97%		132,64%		32,64%		1,853
1980 год	320,047	166,445	74,324		208,36%		130,25%		30,25%		2,457
1981 год	340,405	186,803	20,358		221,62%		106,36%		6,36%		3,200
1982 год	323,143	169,541	-17,262		210,38%		94,93%		-5,07%		3,404
1983 год	324,779	171,177	1,637		211,44%		100,51%		0,51%		3,231
1984 год	351,503	197,902	26,724		228,84%		108,23%		8,23%		3,248
1985 год	350,810	197,208	-0,694		228,39%		99,80%		-0,20%		3,515
1986 год	357,280	203,678	6,471		232,60%		101,84%		1,84%		3,508
1987 год	432,016	278,414	74,736		281,26%		120,92%		20,92%		3,573
1988 год	550,475	396,873	118,459		358,38%		127,42%		27,42%		4,320
1989 год	623,176	469,574	72,701		405,71%		113,21%		13,21%		5,505
1990 год	700,648	547,046	77,472		456,15%		112,43%		12,43%		6,232
1991 год	774,569	620,967	73,921		504,27%		110,55%		10,55%		7,006
1992 год	840,366	686,765	65,797		547,11%		108,49%		8,49%		7,746
1993 год	926,978	773,376	86,612		603,49%		110,31%		10,31%		8,404
1994 год	1074,768	921,166	147,790		699,71%		115,94%		15,94%		9,270
1995 год	1325,392	1171,790	250,624		862,87%		123,32%		23,32%		10,748
1996 год	1400,776	1247,174	75,384		911,95%		105,69%		5,69%		13,254
1997 год	1420,262	1266,660	19,486		924,64%		101,39%		1,39%		14,008
1998 год	1181,367	1027,765	-238,895		769,11%		83,18%		-16,82%		14,203
1999 год	1289,969	1136,367	108,602		839,81%		109,19%		9,19%		11,814
2000 год	1600,160	1446,559	310,191		1041,76%		124,05%		24,05%		12,900
2001 год	1490,788	1337,186	-109,373		970,55%		93,16%		-6,84%		16,002
2002 год	1577,281	1423,679	86,494		1026,86%		105,80%		5,80%		14,908
2003 год	1868,121	1714,519	290,840		1216,21%		118,44%		18,44%		15,773
2004 год	2358,843	2205,241	490,722		1535,69%		126,27%		26,27%		18,681
2005 год	2756,212	2602,610	397,368		1794,39%		116,85%		16,85%		23,588
2006 год	3194,084	3040,482	437,872		2079,46%		115,89%		15,89%		27,562
средний уровень ряда				1011,293		млрд. долларов США
средний абсолютный прирост				104,844		млрд. долларов США
средний темп роста				110,64%
средний темп прироста				10,64%

Таблица 3

Результаты расчетов основных показателей по экспорту

год	Exports	базисный абсолютный прирост, млрд. долларов США	цепной абсолютный прирост, млрд. долларов США		базисный темп роста, %		цепной темп роста,%		темп прироста,%		абсолютное значение одного процента прироста, млрд. долларов США
1977 год	161,610	-	-		-		-		-		-
1978 год	194,927	33,317	33,317		120,62%		120,62%		20,62%		1,616
1979 год	227,777	66,167	32,850		140,94%		116,85%		16,85%		1,949
1980 год	289,523	127,913	61,746		179,15%		127,11%		27,11%		2,278
1981 год	327,218	165,608	37,695		202,47%		113,02%		13,02%		2,895
1982 год	310,594	148,984	-16,624		192,19%		94,92%		-5,08%		3,272
1983 год	327,364	165,754	16,770		202,56%		105,40%		5,40%		3,106
1984 год	378,033	216,423	50,669		233,92%		115,48%		15,48%		3,274
1985 год	382,992	221,382	4,959		236,98%		101,31%		1,31%		3,780
1986 год	436,098	274,487	53,106		269,85%		113,87%		13,87%		3,830
1987 год	524,827	363,216	88,729		324,75%		120,35%		20,35%		4,361
1988 год	625,869	464,259	101,043		387,27%		119,25%		19,25%		5,248
1989 год	677,558	515,948	51,689		419,25%		108,26%		8,26%		6,259
1990 год	736,100	574,490	58,542		455,48%		108,64%		8,64%		6,776
1991 год	831,033	669,423	94,933		514,22%		112,90%		12,90%		7,361
1992 год	923,507	761,897	92,474		571,44%		111,13%		11,13%		8,310
1993 год	1008,911	847,301	85,404		624,29%		109,25%		9,25%		9,235
1994 год	1164,574	1002,964	155,663		720,61%		115,43%		15,43%		10,089
1995 год	1383,224	1221,613	218,650		855,90%		118,78%		18,78%		11,646
1996 год	1399,625	1238,015	16,402		866,05%		101,19%		1,19%		13,832
1997 год	1477,979	1316,369	78,354		914,53%		105,60%		5,60%		13,996
1998 год	1388,101	1226,490	-89,878		858,92%		93,92%		-6,08%		14,780
1999 год	1487,552	1325,942	99,451		920,46%		107,16%		7,16%		13,881
2000 год	1769,469	1607,859	281,917		1094,90%		118,95%		18,95%		14,876
2001 год	1607,824	1446,214	-161,645		994,88%		90,86%		-9,14%		17,695
2002 год	1739,259	1577,648	131,435		1076,21%		108,17%		8,17%		16,078
2003 год	2038,093	1876,483	298,834		1261,12%		117,18%		17,18%		17,393
2004 год	2557,021	2395,411	518,928		1582,22%		125,46%		25,46%		20,381
2005 год	2960,834	2799,224	403,813		1832,08%		115,79%		15,79%		25,570
2006 год	3474,340	3312,730	513,506		2149,83%		117,34%		17,34%		29,608
средний уровень ряда				1093,728		млрд. долларов США
средний абсолютный прирост				114,232		млрд. долларов США
средний темп роста				110,77%
средний темп прироста				10,77%