
- •Понятие функции одного переменного. Виды и способа задания функции
- •2. Предел функции и его свойства
- •3. Односторонние пределы. Существование предела в точке
- •4. Теоремы о пределах функций
- •5. Бесконечно малые и бесконечно большие функции
- •6. Сравнение бесконечно больших и бесконечно малых функций
- •7. Первый и второй замечательные пределы
- •8. Непрерывные и разрывные функции. Классификация точек разрыва. Основные теоремы о непрерывных функциях.
- •9. Понятие производной . Геометрический и физический смысл.
- •10. Понятие дифференцируемости функции в точке. Необходимое и достаточное условие
- •11.Теоремы о производных
- •12. Производная сложной функции.
- •13. Производная обратной функции
- •22. Монотонные функции. Теоремы о функциях непрерывных на отрезках
- •23. Экстремум функции. Необходимые и достаточные условия существования
- •24. Точки перегиба
- •25. Асимптоты
- •26.Алгоритм исследования графиков функций
- •27. Функция двух переменных. Виды и способы задания функции двух переменных
- •28. Предел функции двух переменных в точке
- •30. Непрерывность функции двух переменных в точке
- •31. Частные производные первого порядка
- •32. Дифференцируемость функции двух переменных в точке
- •34. Производная неявной функции
- •35. Производная по направлению
- •37. Частные производные высших порядков
- •39. Признак полного дифференциала
- •40. Экстремумы функций двух переменных.
- •41.Необходимое условие существования экстремума
- •42. Достаточное условие существования экстремума.
- •43. Условный экстремум
- •44. Метод наименьших квадратов.
- •45. Первообразная
7. Первый и второй замечательные пределы
Предел
отношения синуса бесконечно малой дуги
к самой дуге, выраженной в радианах,
называется первым
замечательным пределом.
Этот предел равен единице.

Предел
последовательности

называется
вторым
замечательным пределом.
Этот предел равен числу e:

8. Непрерывные и разрывные функции. Классификация точек разрыва. Основные теоремы о непрерывных функциях.
Фун-ия
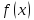 назыв. непрерывной в точке х0,
если
она удовлетворяет 3м условиях: 1)
определена в точке х0
(т.е. сущ-ет
назыв. непрерывной в точке х0,
если
она удовлетворяет 3м условиях: 1)
определена в точке х0
(т.е. сущ-ет
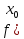 ))
2) имеет конечный предел фун-ии при
))
2) имеет конечный предел фун-ии при
 3) этот предел равен значению фун-ии в
точке х0,
т.е.
3) этот предел равен значению фун-ии в
точке х0,
т.е.

Фун-ия
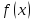 назыв. непрерывной в точке х0,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечное малое
приращение фун-ии:
назыв. непрерывной в точке х0,
если она определена в этой точке и
бесконечно малому приращению аргумента
соответствует бесконечное малое
приращение фун-ии:

Различают
точки разрыва: первого рода (когда
сущ-ет конечные односторонние пределы
фун-ии слева и справа
 ,
не равные друг другу) и второго рода
(когда хотя бы один из односторонних
пределов слева или справа равен
бесконечности или не сущ-ет). К точкам
разрыва первого рода также относятся
точки устранимого разрыва, когда предел
фун-ии при
,
не равные друг другу) и второго рода
(когда хотя бы один из односторонних
пределов слева или справа равен
бесконечности или не сущ-ет). К точкам
разрыва первого рода также относятся
точки устранимого разрыва, когда предел
фун-ии при
 сущ-ет, но не равен значению фун-ии в
этой точке.
сущ-ет, но не равен значению фун-ии в
этой точке.
Теоремы
1)Если
фун-ия
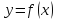 непрерывна на отрезке [a;b],
то она ограничена на этом отрезке
непрерывна на отрезке [a;b],
то она ограничена на этом отрезке
2)Если
фун-ция
 непрерывна на отрезке [a;b],
то она достигает на этом отрезке
наименьшего значения m
и наибольшего значения M
(теорема Вейерштрасса)
непрерывна на отрезке [a;b],
то она достигает на этом отрезке
наименьшего значения m
и наибольшего значения M
(теорема Вейерштрасса)
3)Если
фун-ция
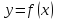 непрерывна на отрезке [a;b]
и значения её на концах отрезка
непрерывна на отрезке [a;b]
и значения её на концах отрезка
 имеют противоположные знаки, то внутри
отрезка найдётся точка
имеют противоположные знаки, то внутри
отрезка найдётся точка
 ,
такая, что
,
такая, что
 (теорема Больцано-Коши)
(теорема Больцано-Коши)
Разрывная функция - функция, имеющая разрыв в некоторых точках
9. Понятие производной . Геометрический и физический смысл.
Производной
фун-ии
 назыв. предел отношения приращения
фун-ии к приращению независимой
переменной при стремлении последнего
к нулю (если этот предел сущ-ет):
назыв. предел отношения приращения
фун-ии к приращению независимой
переменной при стремлении последнего
к нулю (если этот предел сущ-ет):

Нахождении производ. фун-ии назыв. дифференцированием этой фун-ии.
Геометрич.
смысл произв-ой: производная
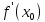 есть угловой коэффициент (тангенс угла
наклона) касательной, проведённой к
кривой
есть угловой коэффициент (тангенс угла
наклона) касательной, проведённой к
кривой

Физич.
смысл производной: производная пути
по времени
 есть скорость точки в момент
есть скорость точки в момент
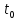 :
:

10. Понятие дифференцируемости функции в точке. Необходимое и достаточное условие
Если фун-ция в точке х имеет конечную производную, то фун-ия назыв. дифференцируемой в этой точке. Функция f(x) называется дифференцируемой в точке х0, если ее приращение представимо в виде:
Δf =f(x0 + Δx)−f(x0) = A·Δx+α(Δх)Δx ,
где A — число, не зависящее от Δх, а α(Δх) – это бмф-я арг Δх
Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. При этом

11.Теоремы о производных
Сформулируем некоторые теоремы о производных.
Теорема.
Если существуют производные
![]() и
и
![]() функций
функций
![]() и
и
![]() ,
то существует
,
то существует
![]()
![]() ;
;
![]()
Следствие.
![]() так
как
так
как
![]() (т.е.
постоянный множитель выносится за знак
производной.
(т.е.
постоянный множитель выносится за знак
производной.
Теорема.
Если функция в точке
![]() имеет
производную, то она в этой точке
непрерывна.
имеет
производную, то она в этой точке
непрерывна.
Обратное
неверно. На рис. 30 изображена непрерывная
функция, у которой в точке
![]() нет
производной.
нет
производной.
Теорема
о производной сложной функции.
Пусть функция
![]() имеет
производную в точке
имеет
производную в точке
![]() ,
а функция
,
а функция
![]() имеет
производную в точке
имеет
производную в точке
![]() .
Тогда сложная функция
.
Тогда сложная функция
![]() имеет
производную в точке
имеет
производную в точке
![]() ,
причем
,
причем
![]() .
.
Короче:
![]() в
произвольной точке
в
произвольной точке
![]() .
.
